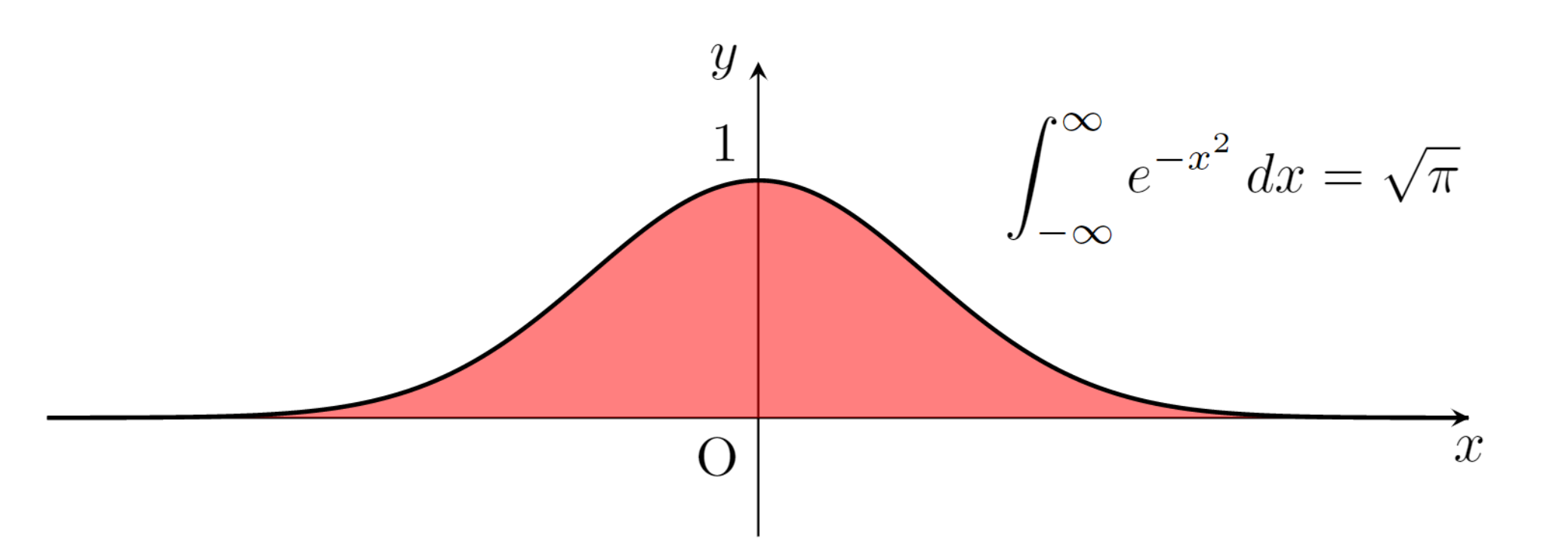
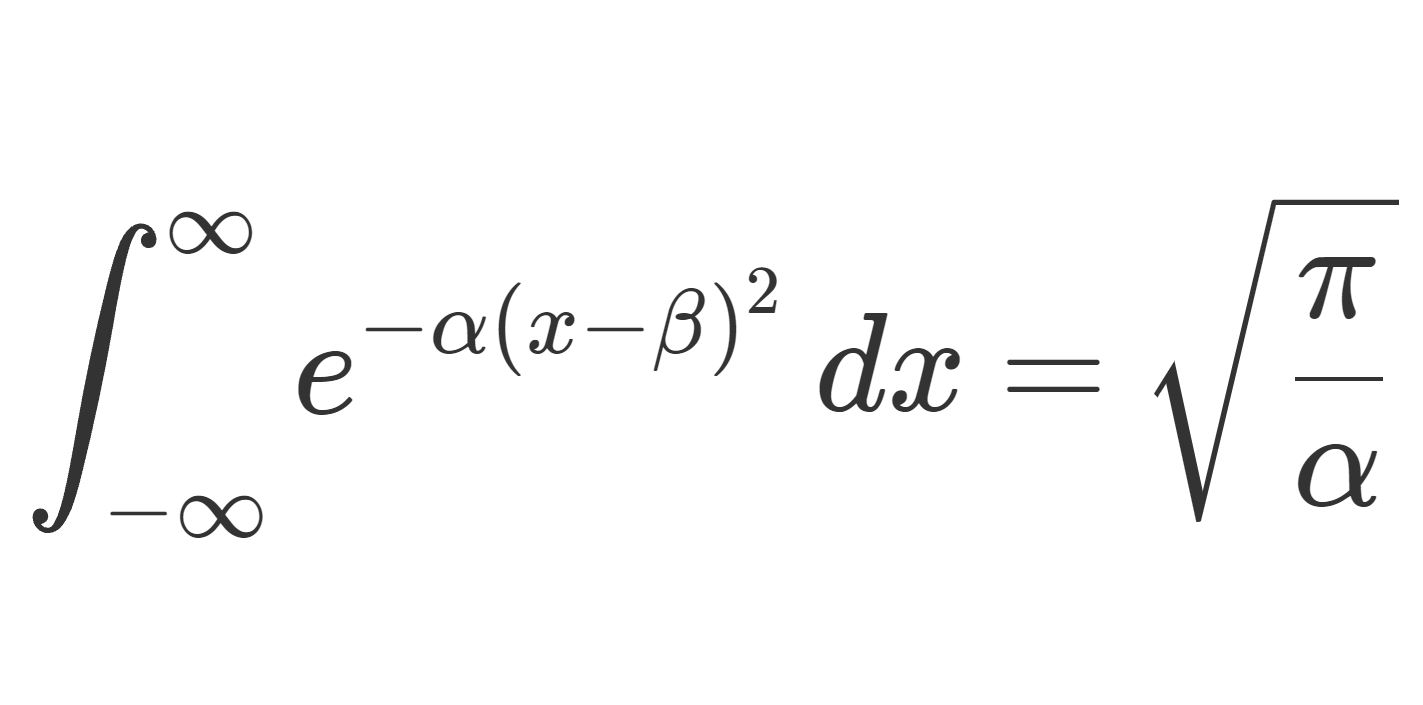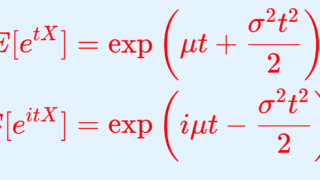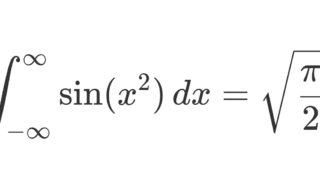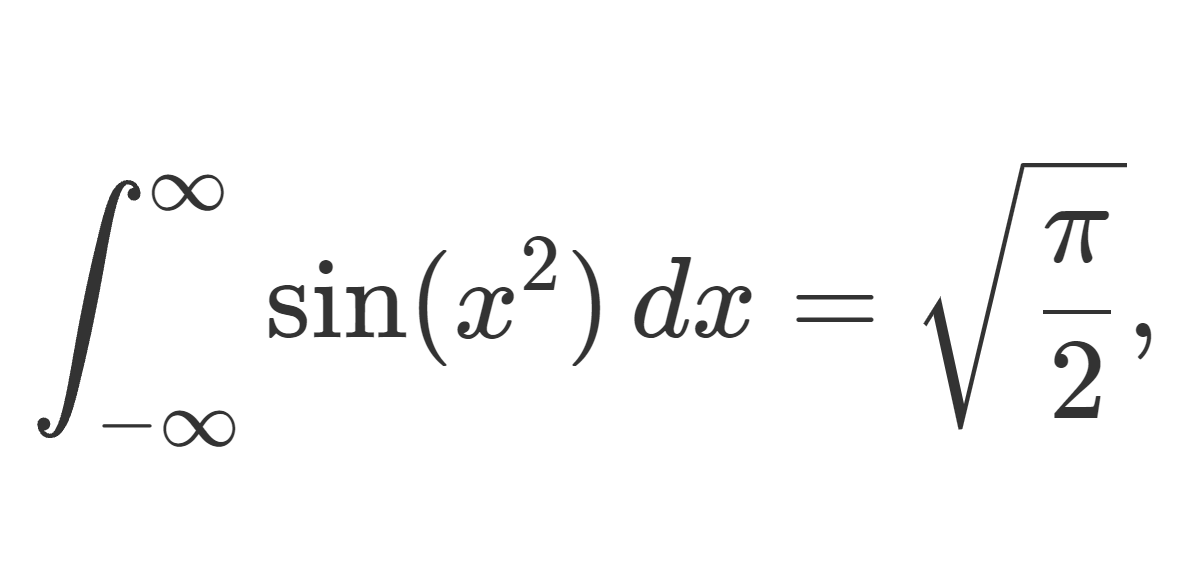ガウス積分の指数部分を複素数に拡張したものは, \operatorname{Re} \alpha > 0,\, \beta \in \mathbb{C} に対して,
\int_{-\infty}^\infty e^{-\alpha(x-\beta)^2}\,dx=\sqrt{\frac{\pi}{\alpha}}
となります。これについて,その導出を行いましょう。
複素数版のガウス積分
実数版のガウス積分は a>0,\,b\in\mathbb{R} に対して
\int_{-\infty}^\infty e^{-a(x-b)^2}\,dx = \sqrt{\frac{\pi}{a}}
です。これは以下で解説しています。
これを複素数に拡張したものが,次の定理です。
定理(複素ガウス積分)
\operatorname{Re} \alpha > 0,\, \beta \in \mathbb{C} に対して,
\large\color{red}\int_{-\infty}^\infty e^{-\alpha(x-\beta)^2}\,dx=\sqrt{\frac{\pi}{\alpha}}
が成り立つ。
複素ガウス積分には身近な応用があります。正規分布の特性関数の計算には,複素ガウス積分を用いる必要があります。
複素数版のガウス積分の導出
早速導出していきましょう。
\int_{-\infty}^\infty e^{-a(x-b)^2}\,dx = \sqrt{\frac{\pi}{a}},\quad a>0,\,b\in\mathbb{R}
について,
- まず b\in\mathbb{R} を \beta\in\mathbb{C} に拡張し,
- それから a>0 を \alpha \in \{ \operatorname{Re} \alpha>0\} に拡張
するかたちで証明します。
1. bを複素数βに拡張する証明
さて,まずは (x-b)^2 の b\in\mathbb{R} を (x-\beta)^2\;(\beta\in\mathbb{C}) に拡張しましょう。経路積分の議論を用います。
証明
積分のシフトにより, b\in\mathbb{R} に対して,
\int_{-\infty+ib}^{\infty+ib} e^{-az^2}\,dz = \sqrt{\frac{\pi}{a}}
を示せばよい。 R_1,R_2>0 とし,下のような経路 C で周回積分すると, \int_C e^{-az^2}\,dz =0 である。
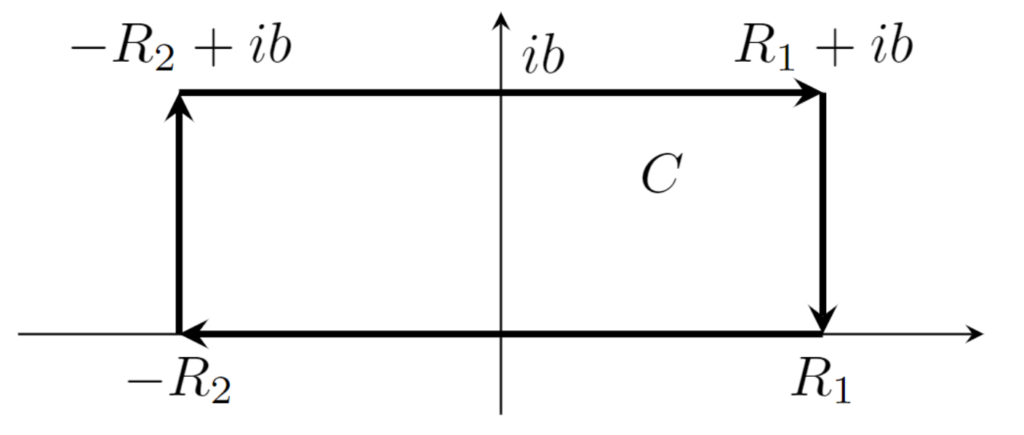
よって,
\small \!\!\left(\int_{-R_2+ib}^{R_1+ib} \!+\! \int_{R_1+ib}^{R_1}\!+\! \int_{R_1}^{-R_2}\! +\!\int_{-R_2}^{-R_2+ib} \right)e^{-az^2}\,dz =0.
ここで,
であり,同様に
であるから,等式で R_1,R_2\to\infty とすることで,
がわかる。
証明終
これで,無事に a>0, \, \beta\in\mathbb{C} に対して
\begin{equation*} \int_{-\infty}^\infty e^{-a(x-\beta)^2}\,dx=\sqrt{\frac{\pi}{a}} \end{equation*}
が証明できたことになりますね。
2. aを複素数αにする証明
a>0, \, \beta\in\mathbb{C} のときに証明した
\begin{equation} \int_{-\infty}^\infty e^{-a(x-\beta)^2}\,dx=\sqrt{\frac{\pi}{a}} \end{equation}
の両辺を, \operatorname{Re}\alpha>0 に解析接続する形で証明しましょう。
証明
積分のシフトにより,\beta = -ib\;(b\in\mathbb{R}) (純虚数または 0)と思ってもよい。
\alpha \mapsto \int_{-\infty}^\infty e^{-\alpha (x+ib)^2}\,dx が, \operatorname{Re}\alpha>0 上解析的(正則)であることを示そう。右辺を f(\alpha) とおくと, |h|<\min\{ \operatorname{Re} \alpha, |\operatorname{Im} \alpha|\}/2 をみたす h\in\mathbb{C} に対して,
\begin{equation}\begin{aligned} &\frac{f(\alpha+h)-f(\alpha)}{h}\\ &= \int_{-\infty}^\infty \frac{e^{-(\alpha+h)(x+ib)^2}-e^{-\alpha(x+ib)^2}}{h}\,dx. \end{aligned}\end{equation}
このとき,被積分関数について,
ここで, \alpha=s+it,\, y=p+iq\;(s,t, p,q\in\mathbb{R}) とおくと,指数部分について
であるから,
となって, s>0 なので,これは x\in (-\infty,\infty) 上可積分な関数である。ルベーグの収束定理より,(2) 式は h\to 0 で収束する。よって, f(\alpha) は \operatorname{Re}\alpha>0 上解析的(正則)である。
また, \alpha \mapsto \sqrt{\pi/\alpha} は \operatorname{Re} \alpha>0 上明らかに解析的(正則)であるから, (1) 式は解析接続できて, \operatorname{Re} \alpha>0 上
\int_{-\infty}^\infty e^{-\alpha(x-\beta)^2}\,dx=\sqrt{\frac{\pi}{\alpha}}
が言えた。
証明終
フレネル積分
ガウス積分 \int_{-\infty}^\infty e^{-\alpha x^2}\,dx=\sqrt{\pi/\alpha} は,\operatorname{Re}\alpha>0 でした。しかし,このような \beta =0 のときは, \operatorname{Re}\alpha=0 に拡張することが可能です。これはフレネル積分と呼ばれ,以下で解説しています。