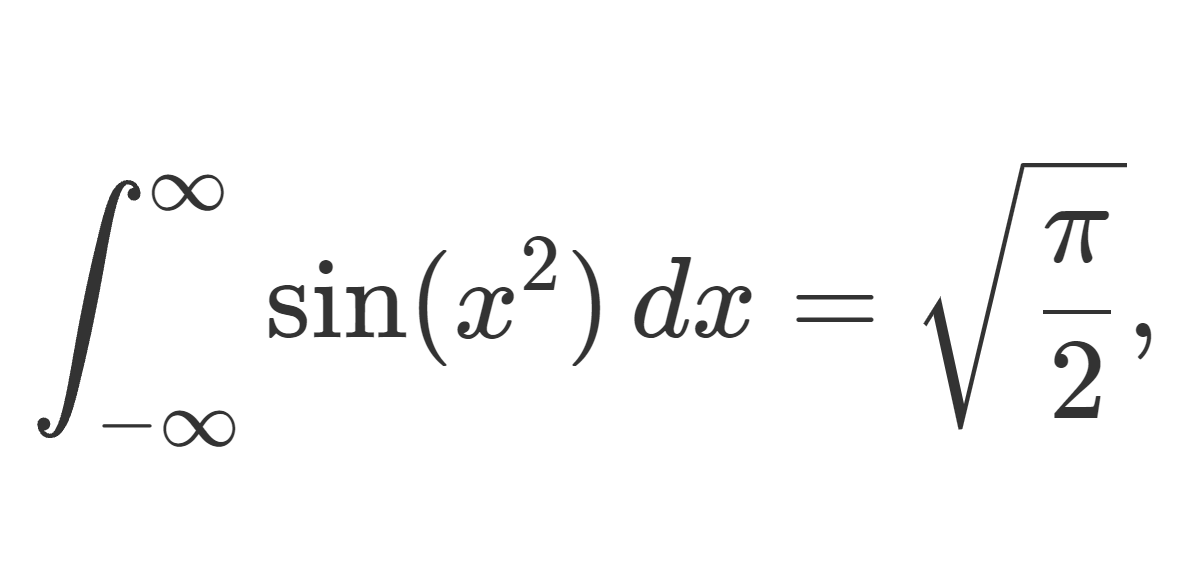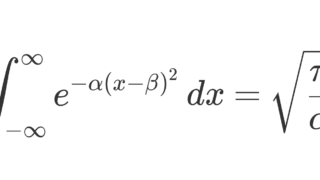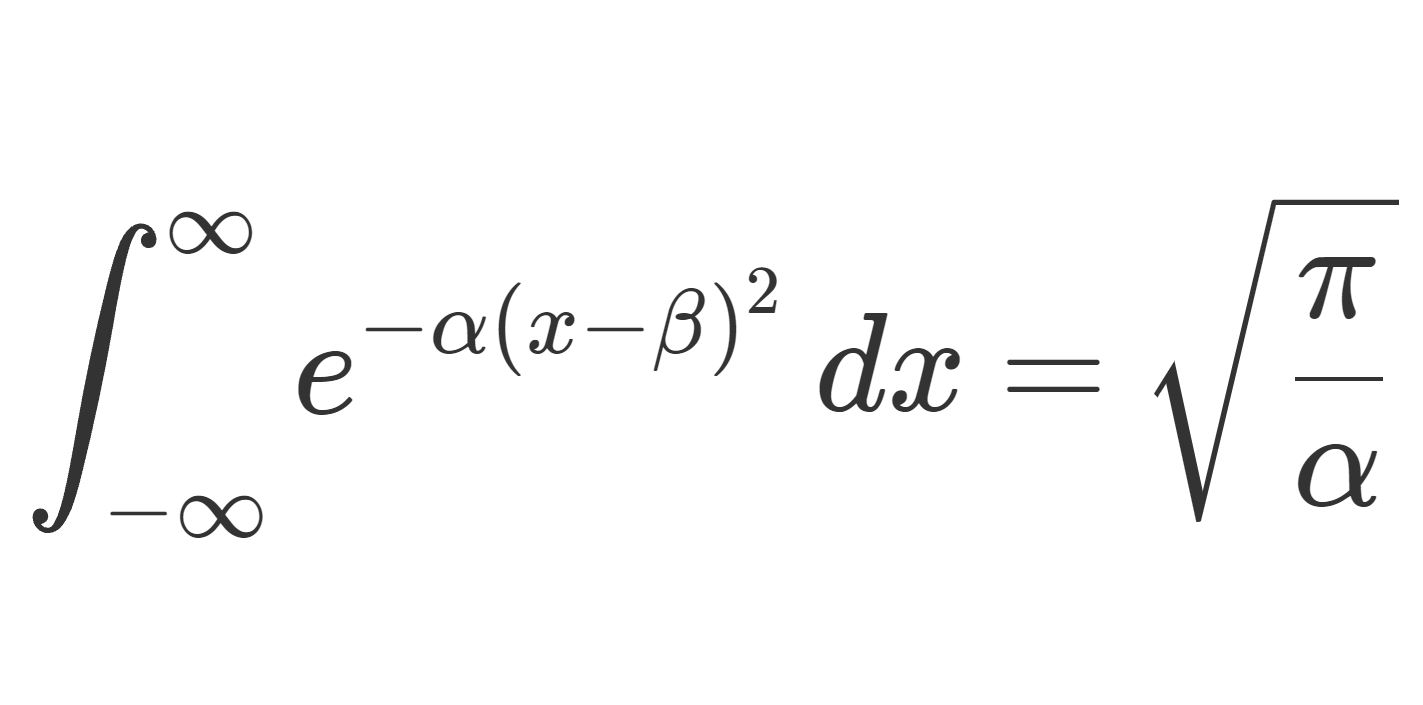フレネル積分は,
\begin{gathered}\int_{-\infty}^\infty \sin(x^2)\,dx = \int_{-\infty}^\infty \cos(x^2)\,dx = \sqrt{\frac{\pi}{2}},\\ \int_{-\infty}^\infty e^{ix^2}\,dx =\sqrt{i\pi}=\sqrt{\frac{\pi}{2}}(1+i) \end{gathered}
のような積分を指し,これは,複素関数論の議論で証明できます。フレネル積分について,その公式と証明を紹介しましょう。
フレネル積分(sin(x^2)の積分)
考えるのは, (\sin x)^2 の積分ではなく, \sin(x^2) の積分です。
定理(フレネル積分;Fresnel integral)
\color{red}\begin{gathered}\int_{-\infty}^\infty \sin(x^2)\,dx = \int_{-\infty}^\infty \cos(x^2)\,dx = \sqrt{\frac{\pi}{2}},\\ \int_{-\infty}^\infty e^{ix^2}\,dx =\sqrt{i\pi}=\sqrt{\frac{\pi}{2}}(1+i) \end{gathered}
である。被積分関数は偶関数なので,
もわかる。 y^2=ax^2 で置換することで, a>0 に対して
もわかる。同様に, a>0 に対して,
もわかる。
e^{ix^2}=\cos (x^2)+i\sin (x^2) ですから,\int_{-\infty}^\infty e^{ix^2} \,dx が求まれば,それの実部・虚部を取り出す形で \int_{-\infty}^\infty \cos(x^2) \,dx や \int_{-\infty}^\infty \sin (x^2)\,dx も求まりますね。
一番最後の積分は,複素ガウス積分における
\int_{-\infty}^\infty e^{-\alpha x^2}\,dx =\sqrt{\frac{\pi}{\alpha}}\quad (\operatorname{Re}\alpha>0)
を, \alpha = ia\;(a\in\mathbb{R}) に拡張した形になっています。(関連記事:複素数版のガウス積分とその導出証明)
なお,上で取り上げた積分は,原始関数が初等関数でかけません。そこで,不定積分を
\begin{aligned} S(x)&= \int_0^x \sin(t^2)\,dt,\\ C(x)&= \int_0^x \cos(t^2)\,dt \end{aligned}
とおいて,利用することがあります。具体的には,光学的応用があるようです。
フレネル積分の導出証明
さて,証明していきましょう。
\int_{0}^\infty e^{ix^2}\,dx =\sqrt{\frac{\pi}{8}}(1+i)
を示せば,残りの式は全て従いますから,これを示すことにしましょう。複素関数論でよくやる経路積分の議論を行います。
証明
f(z)=e^{iz^2} とすると,これは \mathbb{C} 上正則関数である。これを,下のような経路 C_R で積分することを考える。
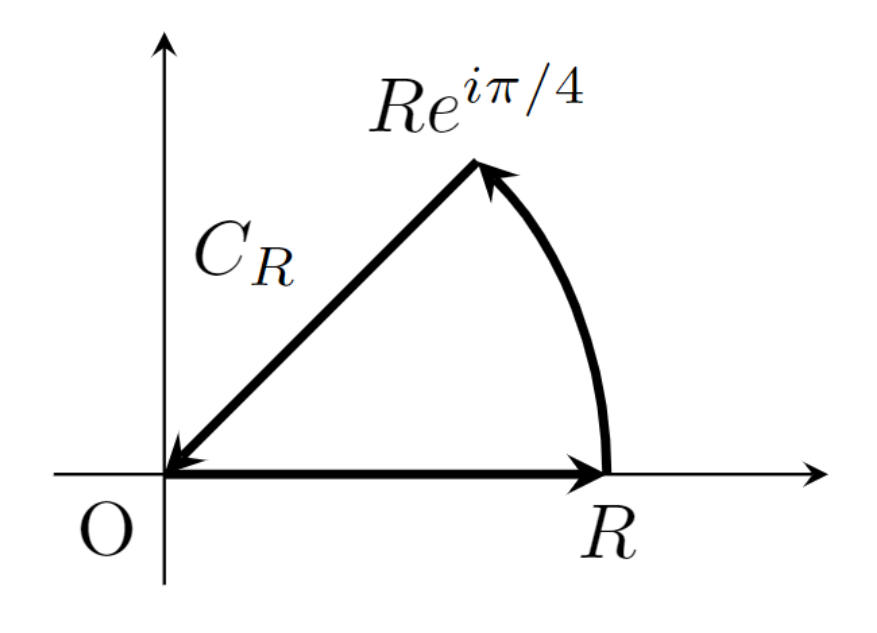
留数定理より,\int_{C_R} f(z)\,dz = 0,すなわち,
\begin{aligned}\int_0^R e^{ix^2}\,dx + \int_0^{\pi/4} e^{iR^2 e^{2i\theta} }Rie^{i\theta}\,d\theta\\ +\int_R^0 e^{i(xe^{i\pi/4})^2}e^{i\pi/4}\,dx =0. \end{aligned}
すなわち,
左辺の第二項について,
であるから,上の等式の両辺を R\to\infty とすることで,
ガウス積分の公式 \int_0^\infty e^{-x^2}\,dx =\sqrt{\pi}/2 より,結論を得る。
証明終
無事に証明できましたね。