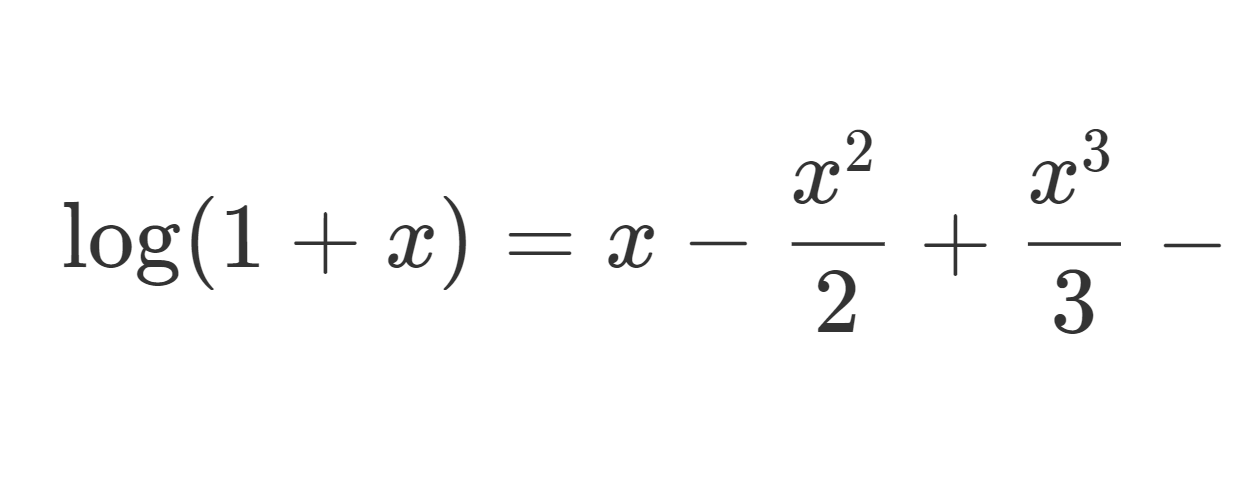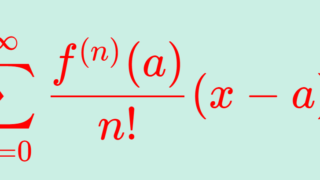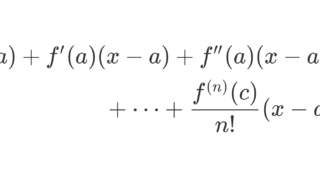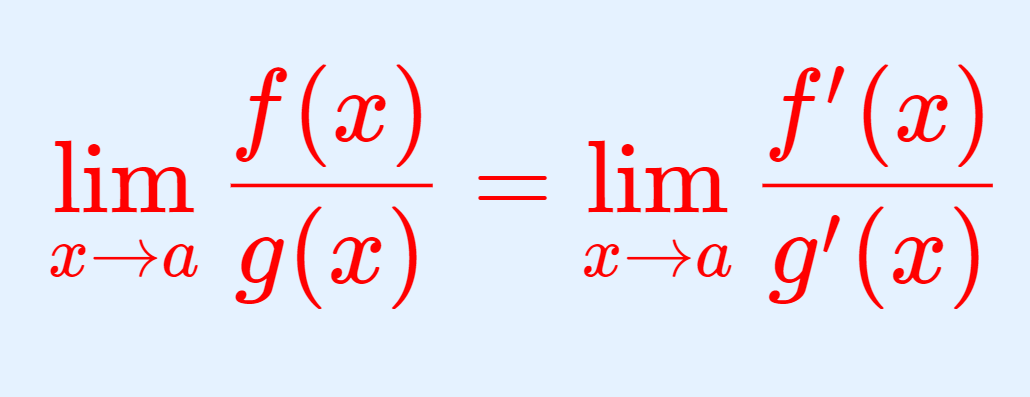\log (1+x) について, 0 を中心とするテイラー展開,すなわちマクローリン展開を考えると,
\small \displaystyle \log(1+ x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \dots + (-1)^{n-1} \frac{x^{n}}{n} + \cdots, \,\, (-1<x\le 1)
になります。これの厳密な導出方法と収束する範囲について解説し,それに関連して交代調和級数の話題と,複素数の \log(1+z) についても触れます。
log(1+x)の0でのテイラー展開(マクローリン展開)
もう一度,結論をちゃんと述べておきましょう。
定理( \log(1+x) のマクローリン展開)
\log(1+x) は 0 のまわりでテイラー展開可能,すなわちマクローリン展開可能であり,
\color{red} \small \displaystyle \log(1+ x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \dots + (-1)^{n-1} \frac{x^{n}}{n} + \cdots, \,\, (-1<x\le 1)
である。特に収束半径は 1 である。
これの導出について,考えていきましょう。
log(1+x)の0でのテイラー展開(マクローリン展開)の導出
詳しい導出について
- そもそも0でのテイラー展開(マクローリン展開)とは
- 形式的な導出と収束半径について
- ちゃんとした導出
- 項別積分を用いた理解
の順に紹介していきましょう。
そもそも0でのテイラー展開(マクローリン展開)とは
マクローリン展開の厳密な定義を復習しましょう。
定義(マクローリン展開)
f を C^\infty 級関数(すなわち無限回微分可能)とする。 0 の近くで
\small\color{red} \begin{aligned} f(x) ={}& f(0)+ f'(0)x + \frac{f''(0)}{2!}x^2 \\ & \hspace{20pt} + \dots + \frac{f^{(n-1)}(x)}{(n-1)!}x^{n-1} + \textcolor{red}{R_n} \end{aligned}と表したとき, R_n \xrightarrow{n\to\infty} 0 となるならば,
\small \color{red}\begin{aligned} &f(x) = \sum_{n=0}^\infty\frac{ f^{(n)}(0)}{n!} x^n \\ &= f(0) + f'(0)x + \frac{f''(a)}{2!} x^2 + \cdots \end{aligned}
とできる。これを f のマクローリン展開 (Maclaurin expansion) という。
なお,テイラー展開は上において,中心を a に平行移動させたもの,すなわち x を x-a に置き換え, f^{(k)} (0) を f^{(k)}(a) 置き換えたものになります。逆に言うとテイラー展開で a=0 とした特別なものがマクローリン展開なわけですね。
log(1+x)のマクローリン展開の形式的な導出と収束半径
形式的な導出
さて,まずは形式的な導出を考えましょう。マクローリン展開の結論の式
\small \begin{aligned} &f(x) = \sum_{n=0}^\infty\frac{ f^{(n)}(0)}{n!} x^n \\ &= f(0) + f'(0)x + \frac{f''(a)}{2!} x^2 + \cdots \end{aligned}に形式的に当てはめることを考えます。今の場合は f(x)= \log(1+ x) ですね。まず,これの n 階微分について,以下の公式が成立します。
命題( \log(1+x) の微分)
f(x) = \log(1+x) \,\, (x>-1) は C^\infty 級(すなわち無限回微分可能)であり,
\color{red} f^{(n)}(x) = (-1)^{n-1} \frac{(n-1)!}{(x+1)^n}
となる。特に,
である。
n 階微分の証明は,帰納法により証明できます。
ちなみに, f(x)=\log x\,\,(x>0) と定義すると, f^{(n)} (x) = (-1)^{n-1} \frac{(n-1)!}{x^n} になります。ただし,このように定義しても 0 ではテイラー展開できません(マクローリン展開できません)ね。なので \log(1+x) で考えています。
これを用いてマクローリン展開の式に当てはめると,\frac{ f^{(n)}(0)}{n!} x^n = (-1)^{n-1}\frac{x^{n}}{n} であることから,形式的に
\small \displaystyle \log(1+ x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \dots + (-1)^{n-1} \frac{x^{n}}{n} + \cdots
が得られましたね。
収束半径と収束するxの範囲
さて,右辺の級数の収束範囲を考えましょう。これには,以下のダランベールの公式を用います。
べき級数 \displaystyle \sum_{n=0}^\infty a_n x^n に対して,
r =\lim_{n\to\infty} \left|\frac{a_n}{a_{n+1}}\right|
が存在するとき, r は収束半径である。
ダランベールの公式をはじめとする,収束半径の定義と求め方については以下の記事で解説しています。
これを用いると,いまの場合
\left| \frac{1/n}{1/(n+1)}\right| = \frac{n+1}{n} \xrightarrow{n\to\infty} 1
であるため,収束範囲が 1 となることが分かりますね。
1 が収束半径とはどういうことかというと, |x|<1 で収束し, |x|>1 で発散するということです。特に, x=\pm 1 のときについては述べていないことに注意が必要です。従って, x=\pm 1 での収束・発散は別に考える必要があります。
マクローリン展開の式に x=-1 を代入すると 1+ \frac{1}{2} + \frac{1}{3} + \cdots =\infty ですね。このことから, x=-1 では収束しません。
一方で, x=1 を代入すると, 1- \frac{1}{2} + \frac{1}{3} - \cdots となって,これは,各項の絶対値が 0 に収束する交代級数ですから,交代級数の収束性の証明とその具体例より収束することが分かります。
さらに,アーベルの連続性定理を用いると,その収束値が \log (1+x) に x=1 を代入した \log 2 になることもわかります(使わなくても以下の「ちゃんとした導出」からわかります)。
以上から,等式
\log(1+ x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4!}+ \cdots
が \color{red} -1<x\le 1 の範囲で成立することが(形式的にですが)分かりました。
log(1+x)のマクローリン展開のちゃんとした導出
上はあくまで形式的な導出でした。本当はマクローリン展開の定義の赤字部分 R_n \xrightarrow{n\to\infty} 0 となるならば,のところをちゃんと確認せねばなりません。 C^\infty 級(無限回微分可能)でも,必ずしもマクローリン展開できるとは限らないのです。
形式的な導出はあくまで結論の式に当てはめただけで,そもそも R_n \xrightarrow{n\to\infty} 0 となるかどうかの確認ができていないわけです。
早速確認していきたいのですが,ここでマクローリンの定理といわれる定理を紹介します。
f は 0 の近くで n 回微分可能であるとする。このとき,
\small \begin{aligned} f(x) ={}&\sum_{k=0}^{n-1} \frac{f^{(k)}(0)}{k!} x^k +R_n\\ ={}& f(0)+ f'(0)x + f''(0)x^2 \\ & \hspace{50pt} + \dots +R_n \end{aligned}
と表すと, \color{red} R_n = \dfrac{f^{(n)}(c)}{(n-1)!}(x-c)^{n-1}x となる 0<c<x または x<c<0 が存在する(コーシーの剰余項, c は x, n に依存する)。
R_n 部分の表現を得ることができる定理です。マクローリンの定理とその証明については,以下の記事で解説しています。
これを用いて,確かに R_n \xrightarrow{n\to\infty} 0 となることを確認することで,形式的な導出を正当化しましょう。
R_n \xrightarrow{n\to\infty}0 の証明
上のマクローリンの定理により,剰余項について
\begin{aligned}R_n &= \dfrac{f^{(n)}(c)}{(n-1)!}(x-c)^{n-1}x \\ &=(-1)^{n-1} \frac{1}{(c+1)^n}(x-c)^{n-1}x \end{aligned}
となる 0<c<x または -1<x<c<0 が存在する。 -1< x \le 1 とすれば |(x-c)/(c+1)|<1 であるから,
従って, R_n \xrightarrow{n\to\infty} 0 が分かった。
証明終
これにより,形式的な導出が正当化できたわけです。なお,これをもってマクローリン展開の収束範囲が -1< x \le 1 であることもわかりますね。
log(1+x)のマクローリン展開の項別積分を用いた理解
このマクローリン展開を項別積分,すなわち無限級数の各項を積分することを考えて理解してみましょう。
まず |x|<1 の範囲において,無限等比級数の和の公式を用いると,
\color{red} \frac{1}{1+x} = \sum_{n=0}^\infty (-1)^{n}x^n = 1- x + x^2 - x^3 + \cdots
になります。とくに,この式は |x|<1 の範囲で絶対かつ広義一様に(すなわち (-1,1) を含む閉区間上で一様に)収束していますね。
この両辺を -1<x<1 として積分 \int_0^x dy を計算してあげましょう。右辺は項別(項毎)に積分できて,
が成り立ちます。この「積分と無限和の順序交換」を項別積分と言いますが,いまの場合,これはちゃんと数学的に正当化できます。この式をそれぞれ計算することで,
となって,マクローリン展開の式が得られましたね。これが,項別積分を用いた理解です。
\log (1+x) のマクローリン展開をもし覚えるのであれば,この導出で覚えるのが一番明快ではないでしょうか。
交代調和級数の収束値の導出
得られた \log(1+x) のマクローリン展開の式
\small \displaystyle \log(1+ x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \dots + (-1)^{n-1} \frac{x^{n}}{n} + \cdots
は -1 < x\le 1 で収束するわけなので, x=1 を代入することで,
を得ます。右辺は交代調和級数と呼ばれる,有名な級数です。 \log のマクローリン展開を使うことで,交代調和級数の収束値が分かりました。
定理としてまとめておきましょう。
定理(交代調和級数の収束)
\small \color{red}\sum_{n=1}^\infty \frac{(-1)^{n-1}}{n!}= 1-\frac{1}{2} + \frac{1}{3} - \frac{1}{4} +\cdots = \log 2
である。
複素関数としてのlog(1+z)のテイラー展開(マクローリン展開)
複素数の範囲で考えても,同様に 0 でテイラー展開可能です。
定理( \log(1+z) のマクローリン展開)
\log(1+z) は 0 のまわりでテイラー展開可能,すなわちマクローリン展開可能であり, |z| \le 1, \, z\ne -1 に対し,
\color{red} \small \displaystyle \log(1+ z) = z - \frac{z^2}{2} + \frac{z^3}{3} - \frac{z^4}{4!} +\cdots
が成立する。特に,収束半径は 1 である。
\log の複素数バージョンは,これを定義とすることもあります。
また, |z|=1, z\ne 1 で等式が成立することに関しては,右辺が条件収束することと,アーベルの連続性定理からわかります。
右辺が |z| = 1, \, z\ne -1 で条件収束することは,以下のディリクレの定理を参考にしてください。