重積分の変数変換の方法と,その例題を2つ紹介します。まずは2重積分の場合を考え,それから一般の多重積分の場合について述べます。
2重積分の変数変換
まずは,2重積分を考えることにしましょう。
定理(2重積分の変数変換)
D\subset \mathbb{R}^2 を2次元領域とし, \phi, \psi \colon D\to \mathbb{R} は C^1 級とする。
変数変換 x=\phi(u,v),\, y=\psi(u,v) により, xy 平面上の領域 D と uv 平面上の領域 E が1対1にうつり合っているとする。 このとき, D 上広義可積分な連続関数 f(x,y) に対して,
\color{red} \begin{aligned}&\int_D f(x,y)\, dxdy \\ &= \int_E f(\phi(u,v),\psi(u,v))\,\left| \frac{\partial (x,y)}{\partial(u,v)}\right| dudv. \end{aligned}
ただし,
はヤコビアン(ヤコビ行列の行列式)を指す。
ですね。ヤコビアンに絶対値がついていますから,行列式そのものではなく,行列式の絶対値をかけていることに注意してください。
変数変換のための条件がいろいろ付いていますが,学部生がテストで出るような積分に関しては,特に気にしなくても,すべての条件を満たしているでしょう。
1変数の積分の変数変換と比較してみましょう。
| 1変数 | 2変数 |
|---|---|
| x=\varphi(t) | x=\phi(u,v),\; y=\psi(u,v) |
| \begin{aligned}&\int_a^b f(x)\,dx\\ &= \int_{\varphi^{-1}(a)}^{\varphi^{-1}(b)}f(\varphi(t))\frac{dx}{dt}dt\end{aligned} | \begin{aligned}&\int_D f(x,y)\, dxdy \\ &= \int_E f(\phi(u,v),\psi(u,v))\,\left| \frac{\partial (x,y)}{\partial(u,v)}\right| dudv. \end{aligned} |
| dx=\frac{dx}{dt}dt | dxdy= \left| \frac{\partial (x,y)}{\partial(u,v)}\right| dudv |
形を見ると,ほぼ同じだということが分かるでしょう。ヤコビ行列は,普通の関数 \mathbb{R}\to \mathbb{R} の微分を \mathbb{R}^m \to\mathbb{R}^n に拡張したものですから,やっていることはほぼ同じなのです。
唯一,絶対値の有無に違いがありますが,それは,積分に向きがあるかの違いです。1変数の積分は, \int_a^b = -\int_b^a のように向きを考えますが,多変数の積分では,そういったことは普通しないため,絶対値がついています。
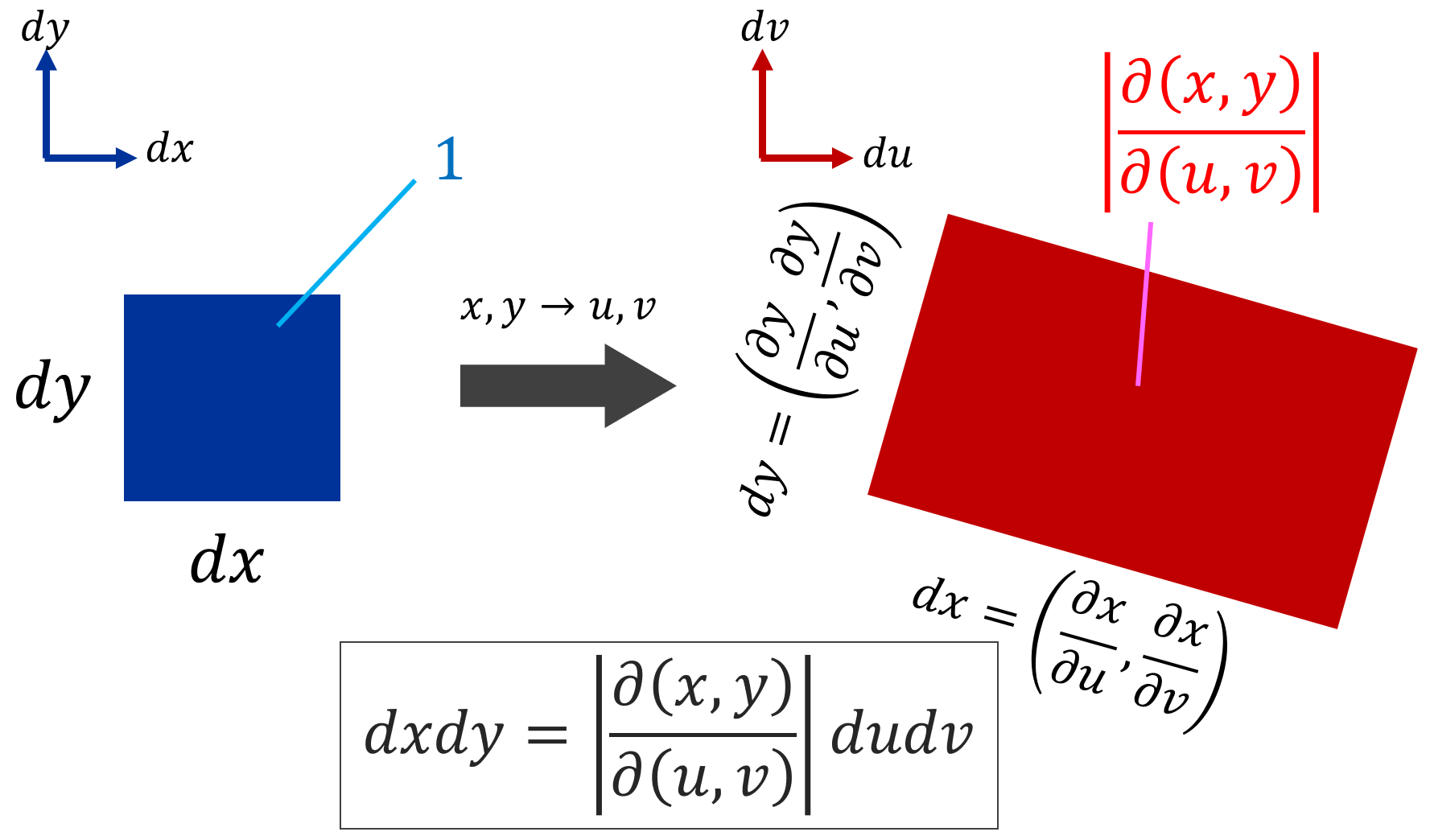
そもそも,1変数の場合の置換積分において, dx=\frac{dx}{dt}dt の dx/dt の部分は,変数変換によって生じるスケール変換を調整するためのものでした。これは,多変数のときも同様です。以下の図を見てください。
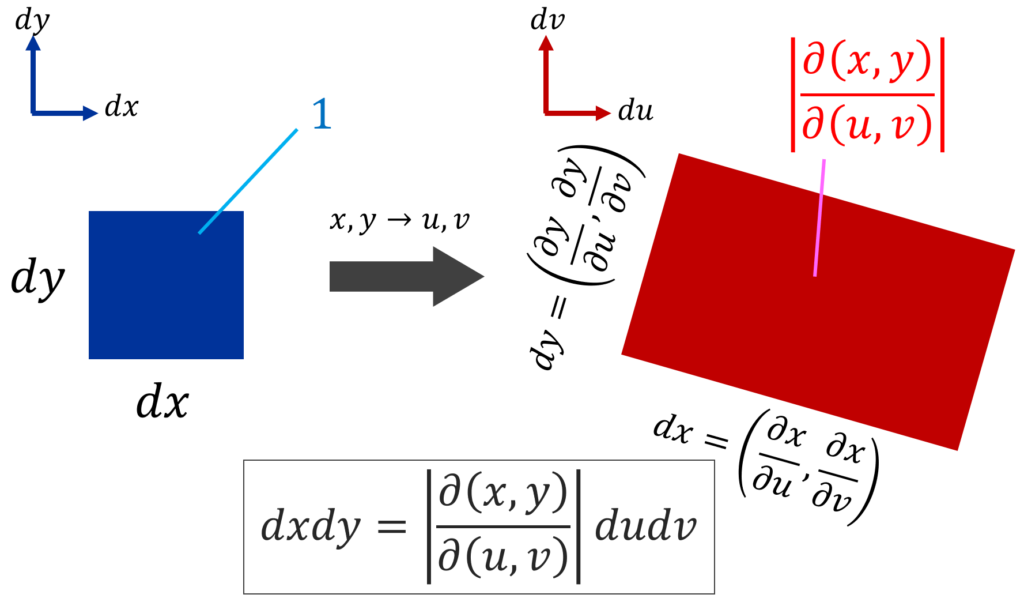
厳密な議論ではありませんが,スケール変換のイメージがつくのではないでしょうか。
2重積分の変数変換の例題
ここからは,例題を考えましょう。
例題1.
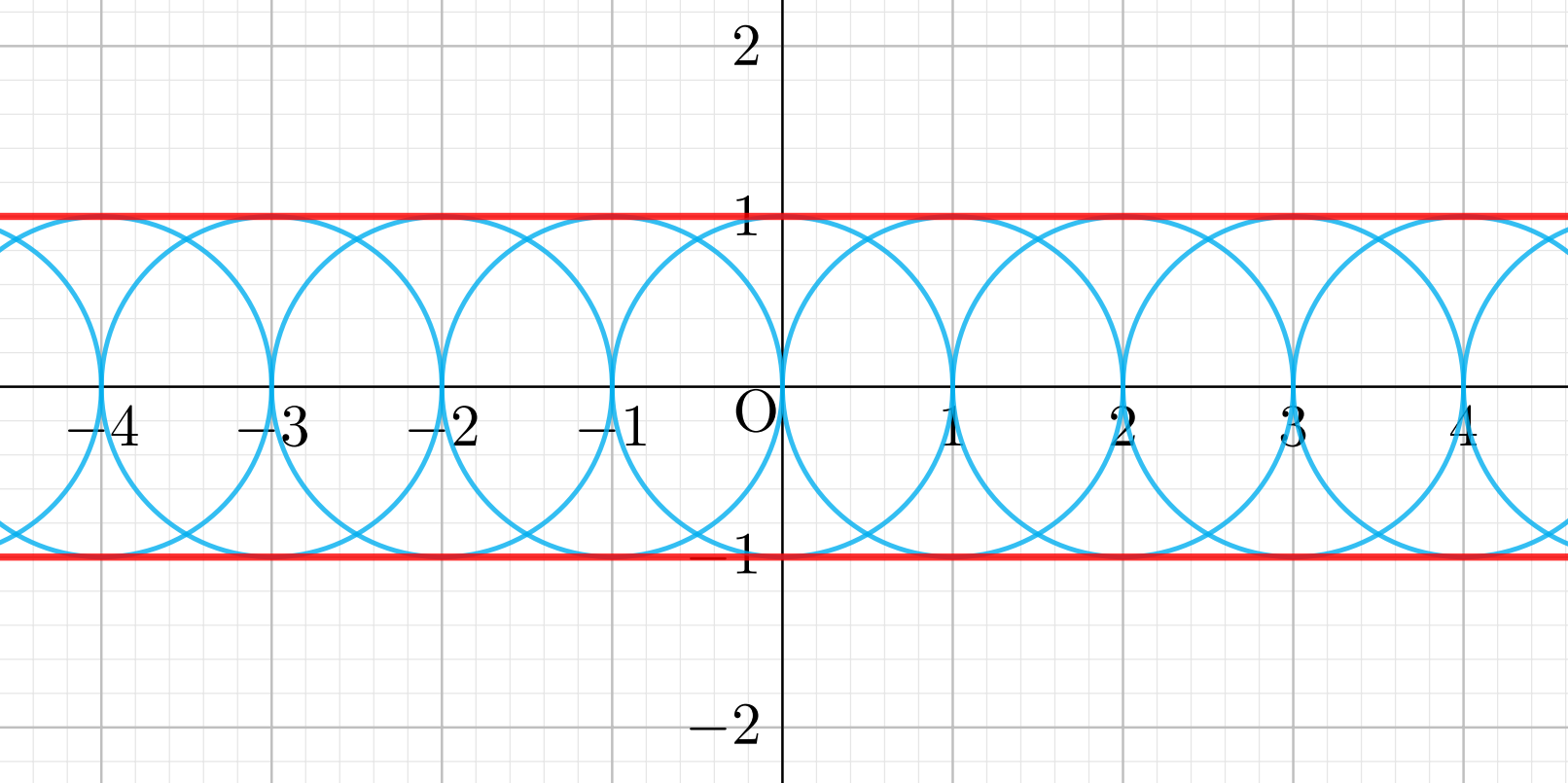
D=\{(x,y)\in\mathbb{R}^2\mid 0\le x+y \le 1,\, 0\le x-y\le 1\} とする。 \displaystyle \iint_D (x^2-y^2)\,dxdy を求めよ。
積分領域 D を図示すると,以下のようになります。
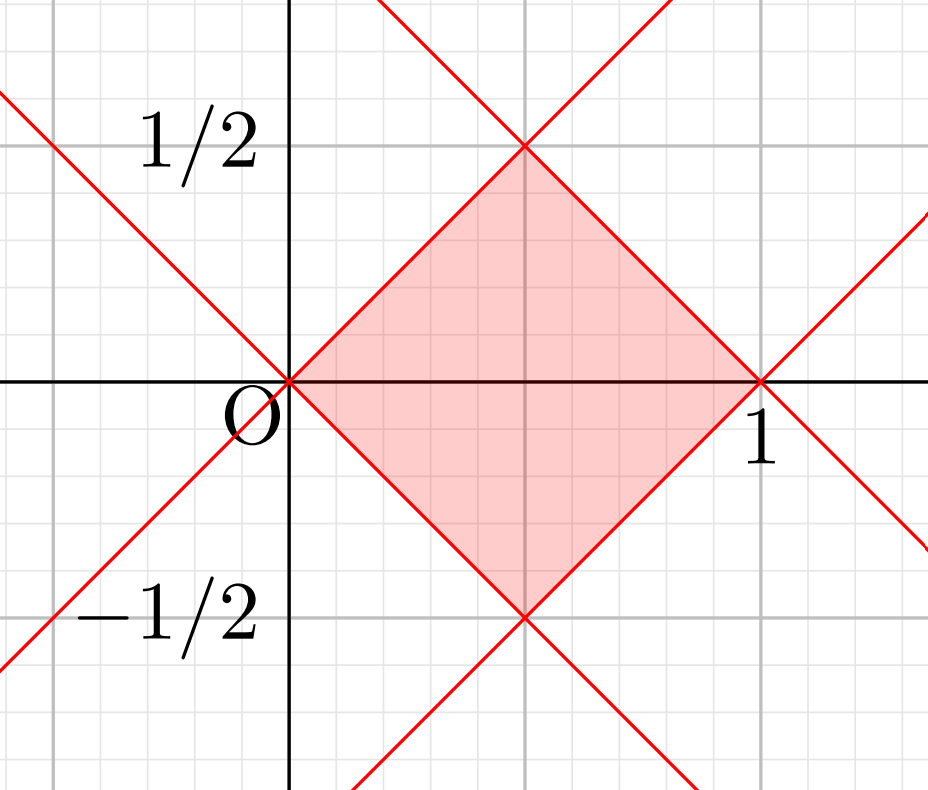
置換積分を用いて解きましょう。
解答
u=x+y,\, v=x-y とする。すなわち, x=(u+v)/2,\, y=(u-v)/2 である。これにより,ヤコビアンについて
\begin{aligned} \frac{\partial (x,y)}{\partial(u,v)} =\det \begin{pmatrix} 1/2 & 1/2 \\ 1/2 & -1/2 \end{pmatrix} =-1/2\end{aligned}
であるから,
例題2.
B=\{ (x,y)\in\mathbb{R}^2\mid x^2+y^2\le 1\} とする。\displaystyle \iint_C \frac{1}{\sqrt{x^2+y^2}}\,dxdy を求めよ。
広義重積分です。これは,極座標変換することで計算できる典型的な問題です。やってみましょう。
解答
x=r\cos\theta, \, y=r\sin\theta \; (r>0) のように極座標変換すると,ヤコビアンについて,
\begin{aligned} \frac{\partial (x,y)}{\partial(r,\theta)} &=\det\begin{pmatrix}\cos\theta & -r\sin\theta \\ \sin\theta& r\cos\theta \end{pmatrix}\\ &= r \cos^2\theta +r\sin^2\theta = r\end{aligned}
であるから,
個人的には, \color{red} \boldsymbol{dxdy=r\,drd\theta} は覚えておくとよいと思います。極座標変換で解く場面は,テストではよくあります。
多重積分の変数変換
変数の数が増えても同様です。多重積分の変数変換を紹介しておきましょう。
定理(多重積分の変数変換)
D\subset \mathbb{R}^n を n 次元領域とし, \phi_1,\dots,\phi_n \colon D\to \mathbb{R} は C^1 級とする。
変数変換 x_1=\phi_1(u_1,\dots,u_n),\, x_n=\phi_n(u_1,\dots, u_n) により,x_1,\dots,x_n に関する領域 D と u_1,\dots, u_n に関する領域 E が1対1にうつり合っているとする。 このとき, D 上広義可積分な連続関数 f(x_1,\dots, x_n) に対して,
\color{red} \begin{aligned}&\!\!\!\!\!\int_D f(x_1,\dots, x_n)\, dx_1\dots dx_n \\ &\!\!\!\!\!= \!\!\int_E f(\phi_1,\dots,\phi_n)\,\left| \frac{\partial (x_1,\dots, x_n)}{\partial(u_1,\dots, u_n)}\right|\, du_1\dots du_n. \end{aligned}
ただし,
はヤコビアン(ヤコビ行列の行列式)を指す。
ですね。