「包絡線」とは,曲線族全てに接しているような曲線のことを言います。これについて,その厳密な定義と,求め方の例題を解説しましょう。
包絡線の定義
パラメータ \alpha を動かすことで,変化する, xy 平面上の曲線 C_\alpha たちを考えましょう。このような「曲線の集まり」 \{C_\alpha \} を曲線族または曲線群といいます。これを踏まえて,包絡線を定義しましょう。
定義(包絡線)
曲線 E が,曲線族 \{C_\alpha\} の全ての曲線に接し,かつ曲線 E の全ての点が,曲線族のいずれかの曲線との接点になっているとき,これを曲線族 \{C_\alpha\} の包絡線 (envelope) という。
全ての曲線族と接し,全ての点がある曲線の接点になっている曲線を包絡線というのですね。
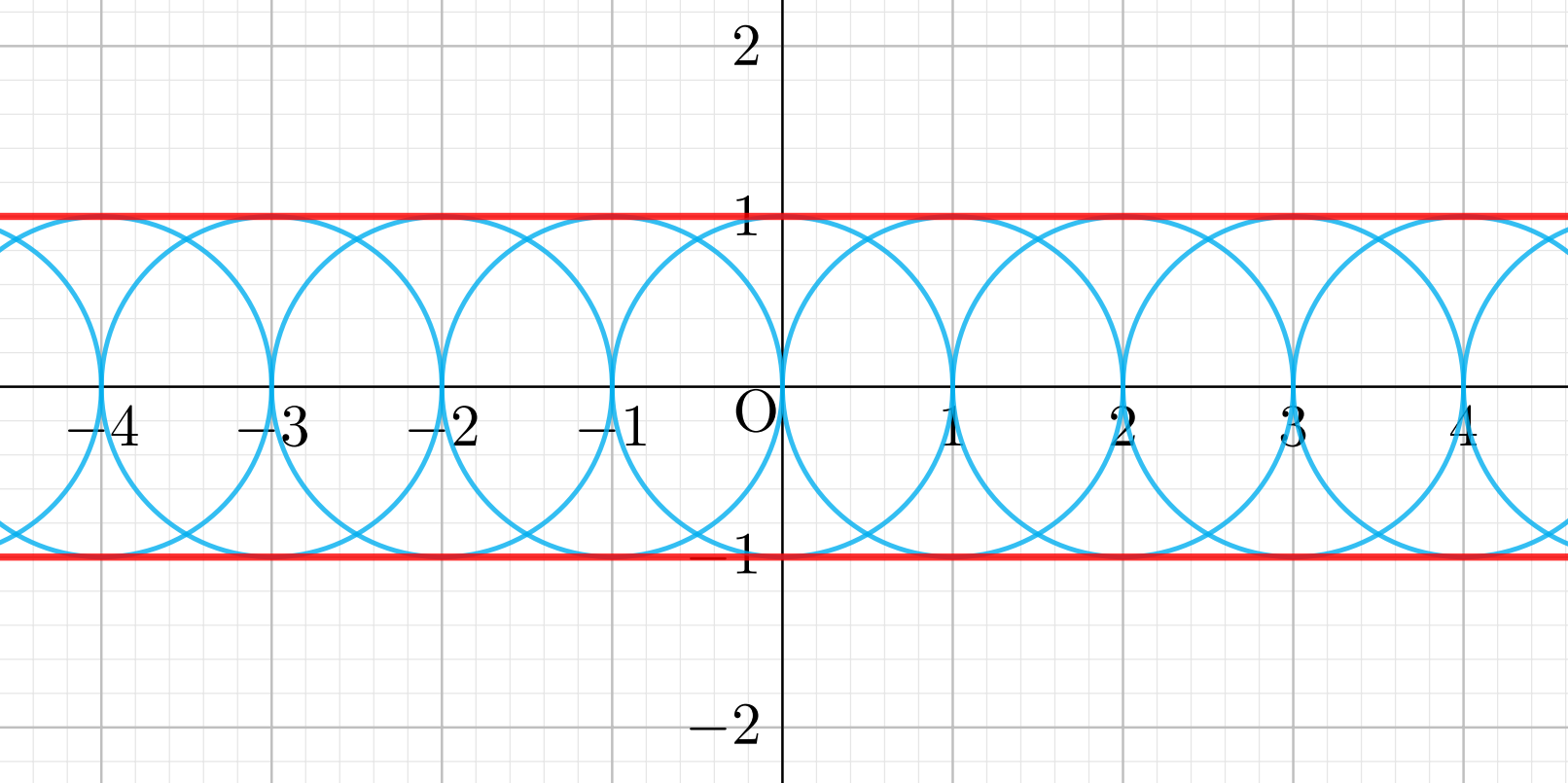
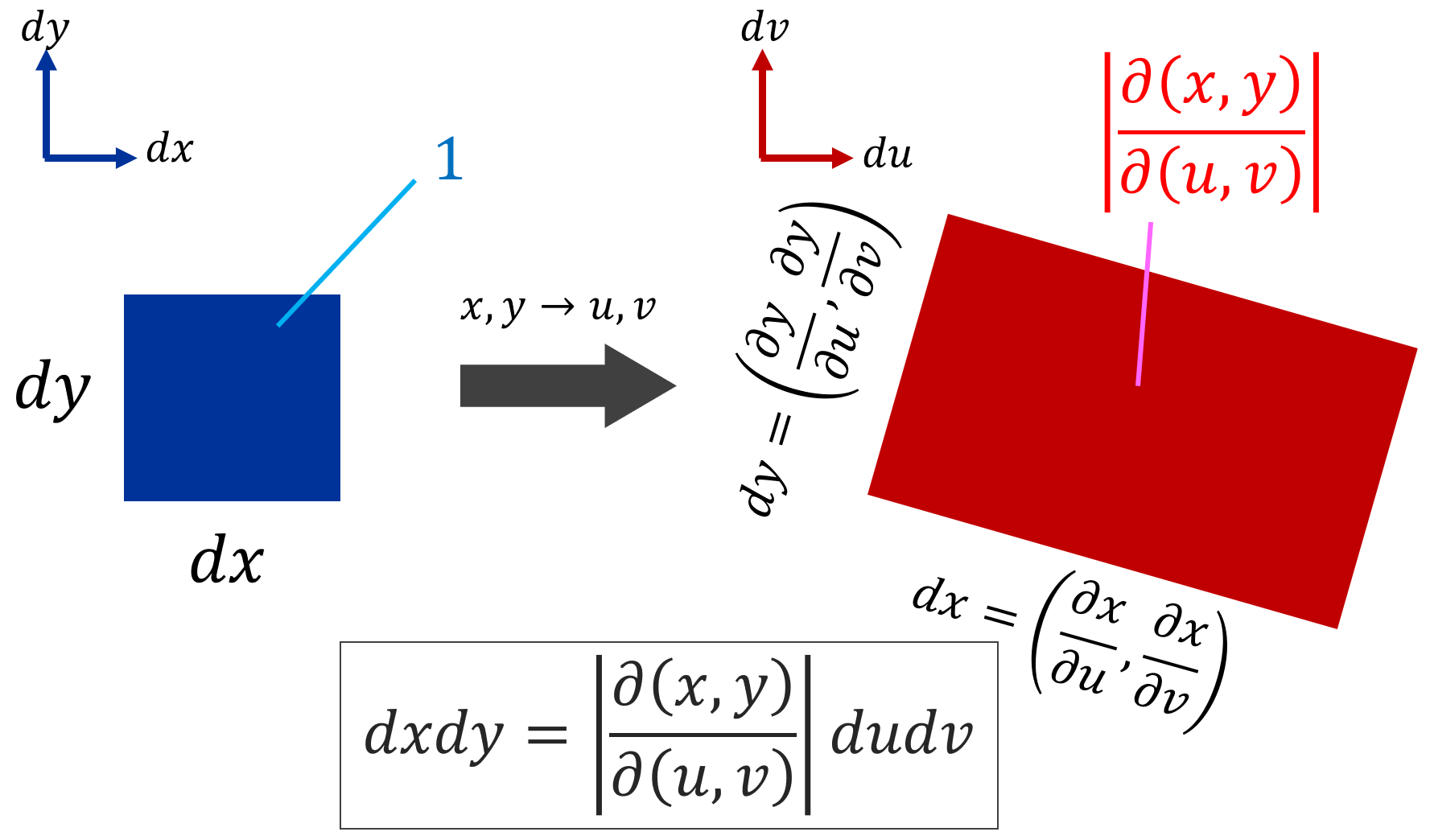
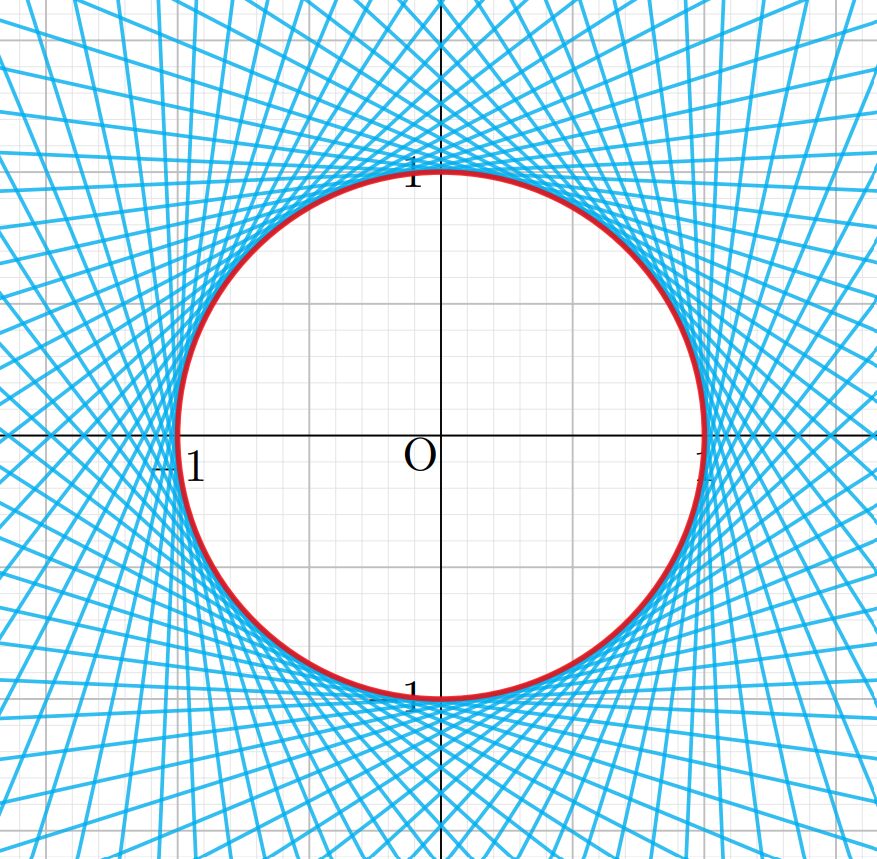
たとえば,以下のような,半径 1 の円の中心が, x 軸上を動く場合を考えましょう。これは,曲線族 C_\alpha\colon (x-\alpha)^2+y^2=1 です。 \alpha を動かすことで,曲線(円)が滑らかに動きます。
この場合の包絡線は,赤線のようになります。包絡線の方程式は, y=\pm 1 ですね。
他にも,さまざまな包絡線を考えることができますから,後で紹介しましょう。
包絡線の求め方と例題
さて,包絡線の求め方とその例題を紹介しましょう。まずは,包絡線を求めるのに用いる定理を紹介します。
包絡線のみたす性質
定理(包絡線のみたす性質)
I\subset \mathbb{R} を開区間とし,曲線 E が曲線族 \{ C_\alpha \colon f_\alpha(x,y)=0\}_{\alpha\in I} の包絡線とする。
さらに, F(x,y,\alpha)= f_\alpha(x,y) は滑らかな関数で,\alpha を変えることで,曲線 C_\alpha と包絡線との接点 (x(\alpha),y(\alpha)) は滑らかに変化するとする。このとき,包絡線の方程式 E(x,y) は
\color{red}F(x,y,\alpha)=\frac{\partial F}{\partial \alpha}(x,y,\alpha)=0\quad(\alpha\in I)
をみたす。
仮定が若干多いですが,「さらに~」の段落は形式的なものなのであまり気にしなくて良いです。
このことから,包絡線の方程式の候補は,連立方程式
\color{red}\begin{dcases} F(x,y,\alpha)=0, \\[5pt] \frac{\partial F}{\partial \alpha}(x,y,\alpha)=0 \end{dcases}からパラメータ \alpha を消去して求めることが可能ということになります。
これを用いて,例題を解いてみましょう。
包絡線を求める例題
例題1.
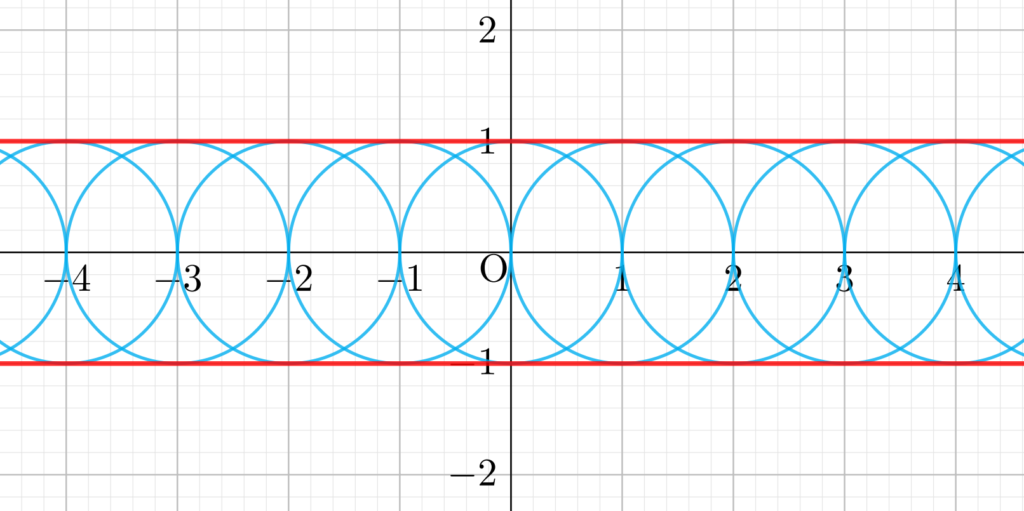
\displaystyle F(x,y,\alpha) =\frac{x^2}{\alpha}+\frac{y^2}{1-\alpha}-1 とおく。曲線族 C_\alpha\colon F (x,y,\alpha)=0 \; (0<\alpha < 1) の包絡線の方程式を求めよ。
今回の曲線族は楕円ですね。楕円の「ゆがみ具合」が \alpha の値によって変わります。
F_\alpha(x,y,\alpha)=0 を計算すると, \displaystyle -\frac{x^2}{\alpha^2}+\frac{y^2}{(1-\alpha)^2}=0 ですから, x/\alpha=\pm y/(1-\alpha) であり,
\alpha=\frac{x}{x\pm y}
となります。これによって F(x,y,\alpha)=0 から \alpha を消去すると,
となるので,図の赤線の包絡線の方程式は, \color{red} x\pm y \pm 1=0, \; |x|,|y|<1 (複号任意)ですね。
例題2.
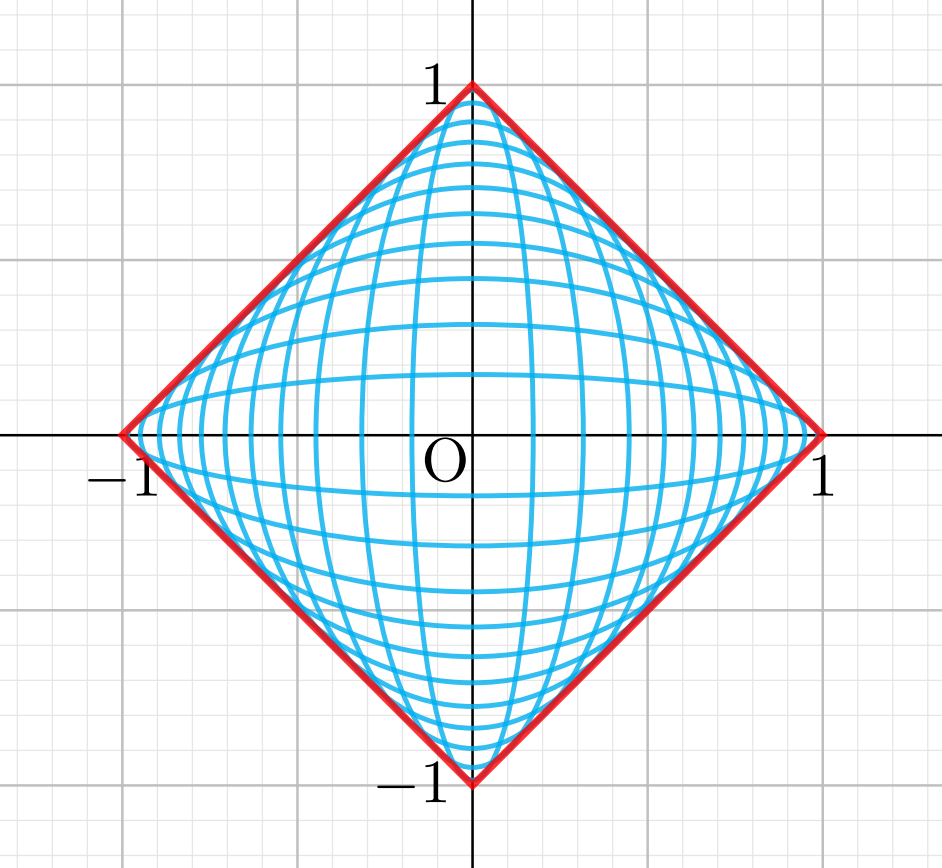
F(x,y,\alpha) = 2\alpha x-y+\alpha^2 とおく。直線族 C_\alpha\colon F(x,y,\alpha)=0 \; (\alpha \in \mathbb{R}) の包絡線の方程式を求めよ。
今回動く図形は直線ですね。下図の赤線が包絡線です。これを求めましょう。
F_\alpha(x,y,\alpha)=0 より, 2x+2\alpha=0 で, \alpha =-x です。これを F(x,y,\alpha)=0 に代入することで, \color{red}y=-x^2 が包絡線の方程式だとわかります。
例題3.
F(x,y,\alpha)=x\cos\alpha+y\sin\alpha-1 とおく。曲線族 C_\alpha\colon F(x,y,\alpha)=0 \;(0\le \alpha<2\pi) の包絡線の方程式を求めよ。
これも,動く図形は直線です。下の図を見る限り,包絡線は円になりそうですね。求めてみましょう。
F_\alpha(x,y,\alpha)=F(x,y,\alpha)=0 を連立することで, x=\cos\alpha, y=\sin\alpha ですから,求める包絡線の方程式は \color{red}x^2+y^2=1 になります。
例題4.
F(x,y,\alpha)=(x-\alpha)^2+y^4-y^2 とする。曲線族 C_\alpha\colon F(x,y,\alpha)=0 の包絡線の方程式を求めよ。
各曲線は,下図のような8の字のようになります。8の字が,左から右に滑らかに動くような感じです。これの包絡線を求めましょう。
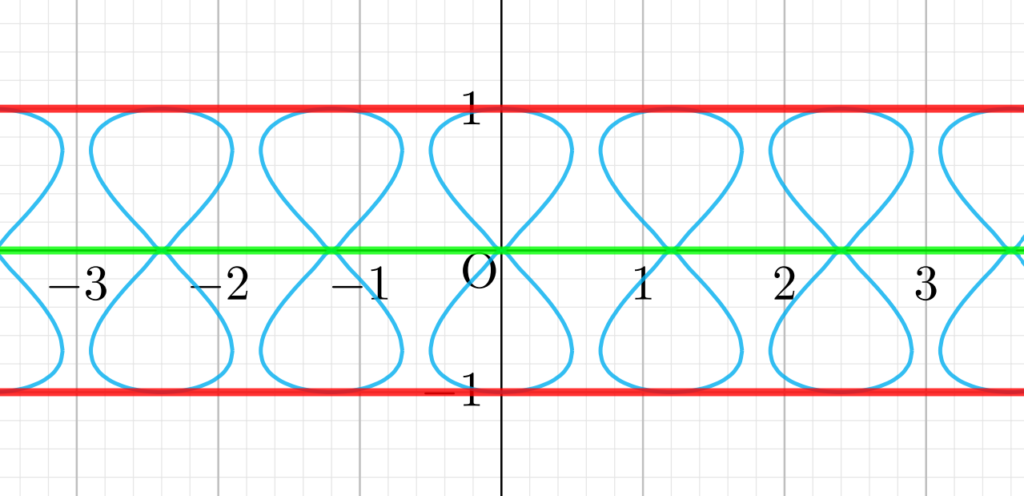
F_\alpha(x,y,\alpha)=0 を考えると, x=\alpha であり,これを F(x,y,\alpha)=0 に代入すると, y^4-y^2=0 になり, y=0,\pm1 になります。図より,包絡線の方程式は \color{red} y=\pm1 ですね。
ここで注意ですが, y=0 (緑の直線) は図から包絡線ではありませんね。連立方程式 F(x,y,\alpha)=F_\alpha (x,y,\alpha)=0 はあくまで包絡線の候補を求めているだけであり,本当に包絡線になっているかは別問題です。
今回の場合,F_x=F_y=0 \iff (x,y)=(\alpha, 0) ですから, y=0 は特異点の軌跡になっています。このように,曲線に特異点がある場合,特異点の軌跡も解として出てきてしまうので注意してください。
包絡線のみたす性質の証明
最後に,包絡線の候補を求めるために用いた定理の証明をしておきましょう。定理を再掲します。
定理の再掲(包絡線のみたす性質)
I\subset \mathbb{R} を開区間とし,曲線 E が曲線族 \{ C_\alpha \colon f_\alpha(x,y)=0\}_{\alpha\in I} の包絡線とする。
さらに, F(x,y,\alpha)= f_\alpha(x,y) は滑らかな関数で,\alpha を変えることで,曲線 C_\alpha と包絡線との接点 (x(\alpha),y(\alpha)) は滑らかに変化するとする。このとき,包絡線の方程式 E(x,y) は
\color{red}F(x,y,\alpha)=\frac{\partial F}{\partial \alpha}(x,y,\alpha)=0\quad(\alpha\in I)
をみたす。
証明
\alpha を固定したときの曲線 F(x,y,\alpha)=0 の接ベクトルは (-F_y,F_x) である。この曲線と包絡線 E の接点を (x(\alpha),y(\alpha)) とすると, E の接ベクトルは (x'(\alpha),y'(\alpha)) である。この2つの接ベクトルが平行であるから,
F_x x'(\alpha)+ F_y y'(\alpha) =0. \tag{1}
一方で, F(x(\alpha),y(\alpha),\alpha)=0 であるから,両辺 \alpha で微分すると,偏微分の連鎖律より,
\text{(2)} - \text{(1)} 式より,
包絡線の方程式が F(x,y,\alpha)=0 をみたすのは明らかであるから,結論を得る。
証明終