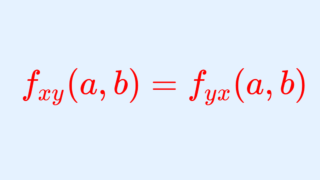偏微分とは～定義と例題と図形的意味～

多変数関数に関して，ある1変数のみを変数とみて，残りの変数を定数と見たときの微分を偏微分と言います。

本記事では，偏微分の定義・例題・図形的意味について，まず $2$ 変数関数の場合を考え，それから $n$ 変数関数の場合を解説しましょう。

2変数関数における偏微分
多変数関数における偏微分
1. 【多変数】偏微分の定義
2. 【多変数】偏微分の計算例題
関連する記事

2変数関数における偏微分

まずは，2変数関数 $f\colon \mathbb{R}^2\to \mathbb{R}$ について，偏微分を導入しましょう。

終域は $\mathbb{R}^2$ ではなく $\mathbb{R}$ であることに注意してください。

【2変数】偏微分への誘い

$f(x,y) = x^2 + 2xy + y^2+3$ という2変数関数を考えましょう。これを， $y$ を定数とみて， $x$ について微分することを考えます。

$y$ を定数とみるとは，たとえば $y=a$ とするとわかりやすいでしょう。
こうすると， $f(x,a) = x^2+ 2ax + a^2+3$ となって，右辺を $x$ について微分すると， $2x+ 2a$ となりますね。

今，わざわざ $y=a$ としましたが， $y$ のままでも変数 $y$ を定数とみることで，微分は $2x+2y$ になることが分かるでしょう。

このように，2変数関数に関して，その1つの変数を定数とし，もう1つの変数で微分したものを「偏微分」といいます。厳密な定義を述べましょう。

【2変数】偏微分・偏導関数の定義

定義（2変数関数の偏微分・偏導関数）

2変数関数 $f(x,y)$ は， $(a,b)\in\mathbb{R}^2$ の周りで定義されているとする。このとき，

\color{red}f_x(a,b) = \lim_{h\to 0} \frac{f(a+h,b)-f(a,b)}{h}

が存在するならば，それを点 $(a,b)\in\mathbb{R}^2$ における $x$ に関する偏微分 (partial derivative) という。これは， $\color{red} f_x(a,b)$ の他に，

\color{red}\partial_x f(a,b),\quad \frac{\partial f}{\partial x}(a,b),\quad \frac{\partial }{\partial x}f(a,b)

などと書かれる。

また，

\color{red} f_x(x,y) = \lim_{h\to 0} \frac{f(x+h,y)-f(x,y)}{h}

が任意の $(x,y)$ で存在するとき， $f_x(x,y)$ を2変数関数とみて，これを $f(x,y)$ の $x$ に関する偏導関数という。

$y$ に関する偏微分

\color{red} f_y(x,y) = \lim_{h\to 0} \frac{f(x,y+h)-f(x,y)}{h}

も同様に定義され， $\displaystyle \color{red}\partial_y f(x,y),\quad \frac{\partial f}{\partial y}(x,y),\quad \frac{\partial }{\partial y}f(x,y)$ も同様に書かれる。

f_x(x,y) = \lim_{h\to 0} \frac{f(x+h,y)-f(x,y)}{h}

の形が， $y$ を定数とみて， $f$ を $x$ で微分した形になっているのが分かるでしょうか。

たとえば， $y$ を定数として， $g(x) = f(x,y)$ としましょう。すると，

\begin{aligned}&\lim_{h\to 0} \frac{f(x+h,y)-f(x,y)}{h}\\&=\lim_{h\to 0} \frac{g(x+h)-g(x)}{h} = \frac{dg}{dx}(x)\end{aligned}

ですから，そうなっていますね。

ここで注意ですが， $f$ が $(a,b)$ で偏微分可能であるからと言って，この点で連続であるとは限りません。あくまで $x\mapsto f(x,b),\; y\mapsto f(a,y)$ の連続性しか言えないです。

【2変数】偏微分・偏導関数の計算例題

早速，具体的な計算を確認してみましょう。

例題1.

$f(x,y) =x^3 + 4x^2 y - 5y^2-2x+3$ とするとき， $f_x(x,y),\; f_y(x,y),\; f_y(1,2)$ をそれぞれ求めよ。

片方の変数を定数とみなしてしまえば，後は1変数のときの計算と全く同じです。計算すると，

\begin{aligned}f_x(x,y) &= 3x^2+8xy-2, \\ f_y(x,y) &= 4x^2-10y \end{aligned}

ですね。また， $f_y$ の式に $(x,y)=(1,2)$ を代入することで，

f_y(1,2) = 4\cdot 1^2 - 10\cdot 2= -16

も分かりますね。

例題2.

$f(x,y)=\dfrac{1}{x^2+y^2+1}$ としたとき，偏導関数 $f_x,f_y$ を求めよ。また， $f_x(1,-1)$ を求めよ。

\begin{aligned} f_x(x,y) &= -\frac{2x}{(x^2+y^2+1)^2} \\ f_y(x,y) &= -\frac{2y}{(x^2+y^2+1)^2}\end{aligned}

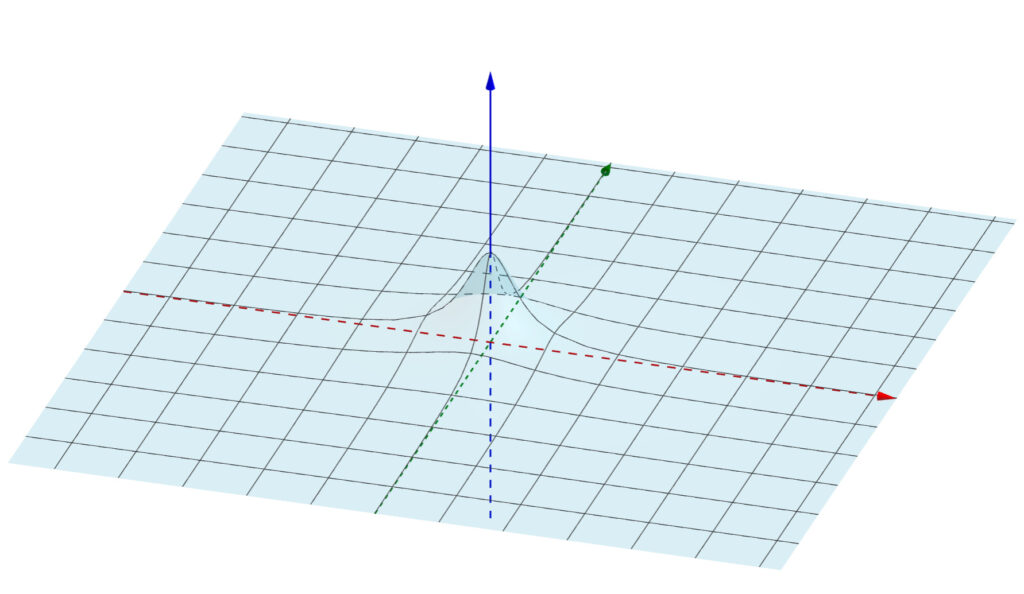
ですね。また，1つ目の式に代入することで， $f_x(1,-1) = -2/9$ もわかります。

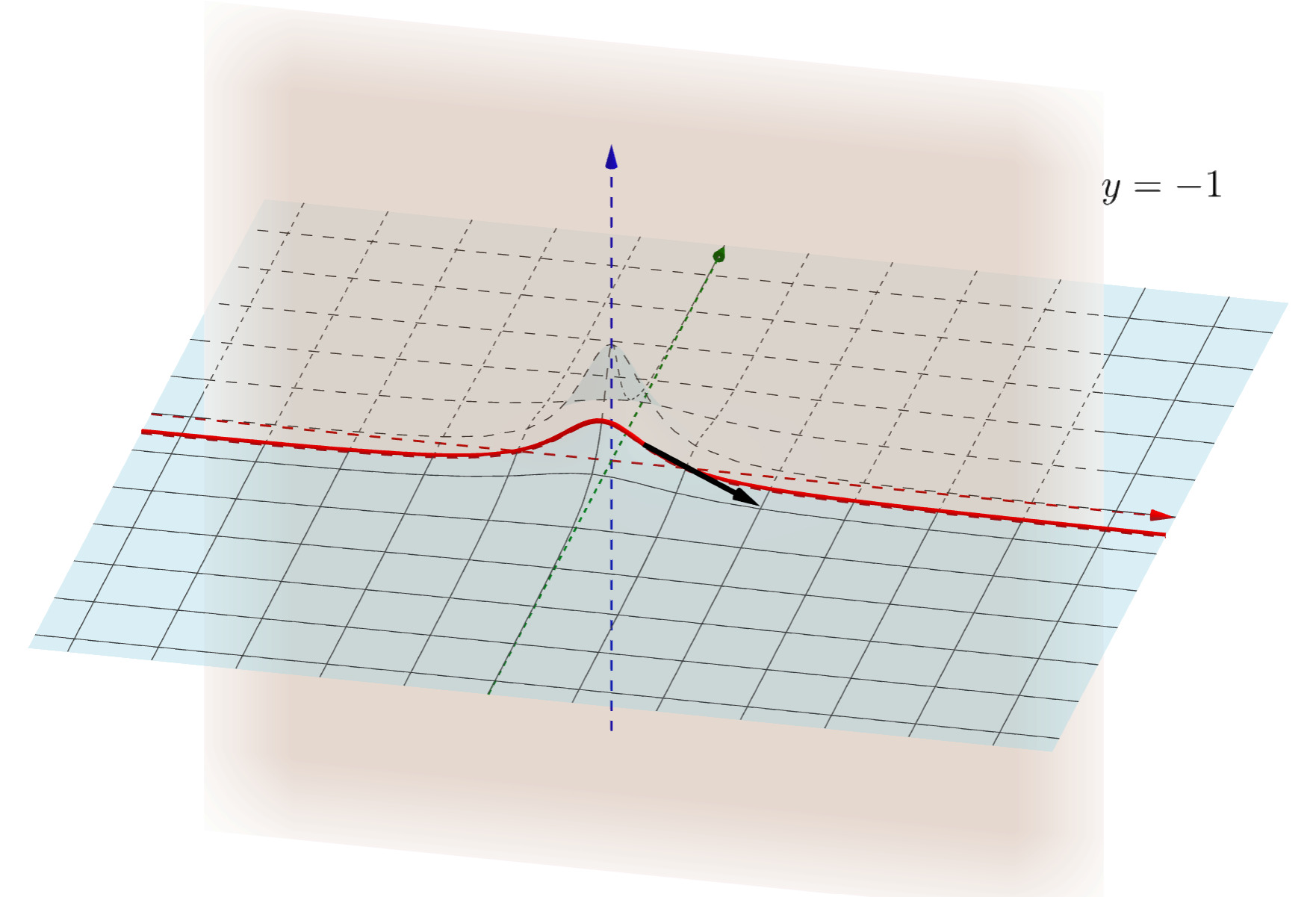
【2変数】偏微分・偏導関数の図形的意味

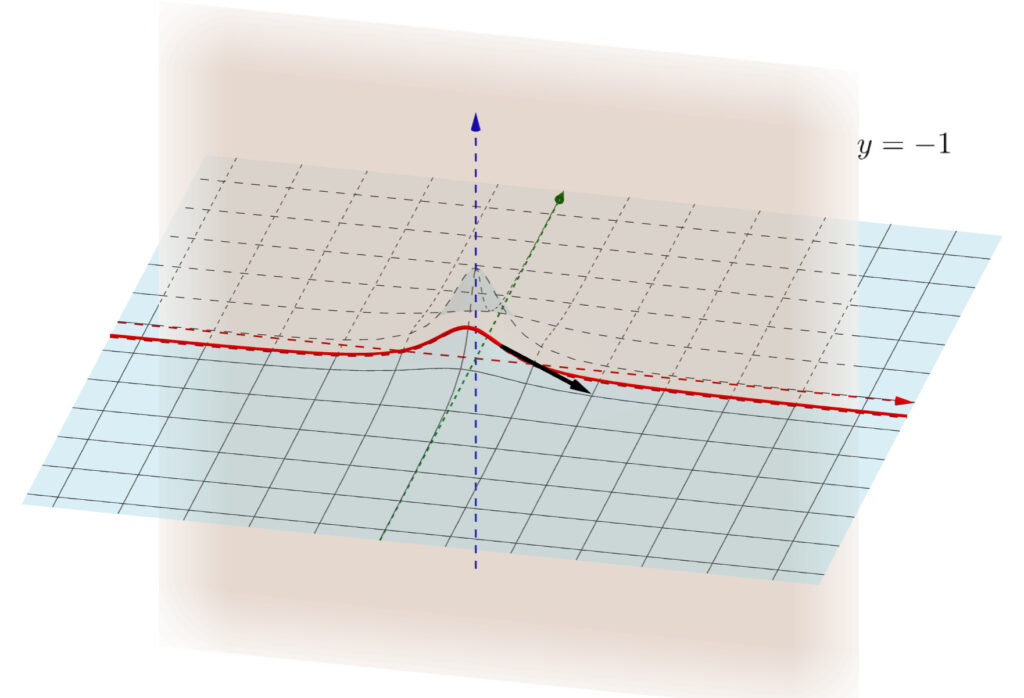
偏微分の図形的意味を考えましょう。図は，例題2を使います。

$y$ を定数とみて $x$ で微分するとは，元のグラフ $z=f(x,y)$ と $y=a$ の交線を考え，その交線の接線の傾きを求める操作に相当します。 $y$ を固定した微分ですから， $z=f(x,y)$ で $y=a$ としてしまった部分にのみ注目して， $xz$ 平面での曲線についての微分のように扱えばよいわけです。

下の図は，例題2において， $f_x(1,-1)$ が表す接線(の傾き)です。

【2変数】高階偏微分の定義

偏導関数 $f_x. f_y$ は，それ自身も2変数関数ですから，その関数が滑らかであれば，さらなる偏微分を考えることができます。

定義（高階偏微分・高階偏導関数）

$f_x$ をさらに $x$ で偏微分した2階偏導関数を

\color{red} \begin{aligned} f_{xx} &= (f_x)_x, & \partial^2_x f &=\partial_{xx} f = \partial_x \partial_x f, \\ \frac{\partial^2 f}{\partial x^2} &= \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x} \right), & \frac{\partial^2}{\partial x^2}f &= \frac{\partial}{\partial x}\frac{\partial }{\partial x} f \end{aligned}

などとかく。 $f_x$ をさらに $y$ で偏微分した2階偏導関数を

\color{red} \begin{aligned} f_{xy} &= (f_x)_y, & \partial_{yx} f &= \partial_y \partial_x f, \\ \frac{\partial^2 f}{\partial y \partial x} &= \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x} \right), & \frac{\partial^2}{\partial y \partial x}f &= \frac{\partial}{\partial y}\frac{\partial }{\partial x} f \end{aligned}

などとかく。また，たとえば

\color{red} \begin{aligned} f_{xyy} &= ((f_x)_y)_y, & \partial_{yyx} f &= \partial^2_y \partial_x f, \\ \frac{\partial^3 f}{\partial y^2 \partial x} &= \frac{\partial^2}{\partial y^2}\left(\frac{\partial f}{\partial x} \right), & \frac{\partial^3}{\partial y^2 \partial x}f &= \frac{\partial^2}{\partial y^2}\frac{\partial }{\partial x} f \end{aligned}

なども同様に定義される。 $f_y$ をさらに偏微分する場合も同じである。

【2変数】高階偏微分の計算例題

高階偏微分の計算も，例を交えて確認していきましょう。

例題3.

$f(x,y) = e^{xy}$ について， $f_{xx}, f_{xy}, f_{yx}, f_{yy}$ をそれぞれ求めよ。

複数回の微分は，1回ずつ微分していくしかないです。今回の場合は，1回微分すると

f_x = ye^{xy}, \quad f_y=xe^{xy}

ですから，

\begin{aligned} f_{xx} &= (f_x)_x = y^2 e^{xy}, \\ f_{xy}&= (f_x)_y = (xy+1)e^{xy},\\ f_{yx} &= (f_y)_x = (xy+1)e^{xy}, \\ f_{yy}&= (f_y)_y =x^2 e^{xy} \end{aligned}

が成り立ちます。

ここで， $f_{xy}=f_{yx}$ が成立していますね。これは，必ずしも一致しているとは限りませんが， $f_{xy}, f_{yx}$ が連続であれば， $f_{xy}=f_{yx}$ が成立することが知られています(→【fxy=fyx】シュワルツの定理とその証明～偏微分の順序交換～)。微分の順番は，多くの場合あまり気にしなくてもよい，ということですね。

多変数関数における偏微分

ここまで2変数で説明してきましたが，より一般に， $f\colon \mathbb{R}^n\to \mathbb{R}$ でも同様に定義できます。1変数のみ変数と見，残りを定数と見た微分を偏微分といいます。

【多変数】偏微分の定義

定義（多変数関数における偏微分）

$n$ 変数関数 $f(x_1,x_2,\dots, x_n)$ について，

\color{red}\begin{aligned}&f_{x_j}(a_1,\dots, a_n) \\&=\lim_{h\to 0} \frac{\begin{aligned}&f(a_1,\dots, a_j + h, \dots, a_n) \\&\qquad - f(a_1,\dots, a_j, \dots, a_n)\end{aligned}}{h}\end{aligned}

( $x_j$ 成分のみ $a_j+h, a_j$ とする)が存在するとき，これを点 $(a_1, \dots, a_n)\in\mathbb{R}^n$ における， $x_j$ に関する偏微分 (partial derivative) といい， $f_{x_j}(x_1,\dots, x_n)$ を $n$ 変数関数と見たもの(が存在するとき，それ)を $x_j$ に関する偏導関数という。

高階偏微分 $\dfrac{\partial^{j_1+\dots +j_n} }{\partial x_1^{j_1}\dots \partial x_n^{j_n}}f$ も(存在すれば)同様に定義可能です。