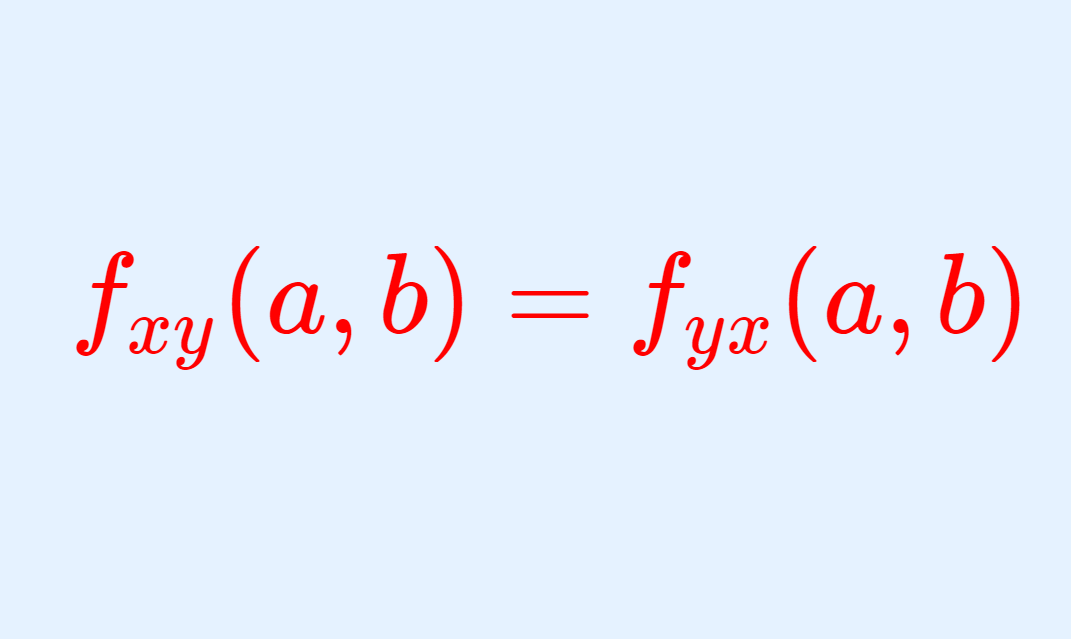多変数関数における全微分とは,関数の1次近似と言えます。これについて,定義・図形的意味・性質・求め方を詳しく解説します。まずは2変数関数で扱い,最後にn変数関数の場合について述べます。
全微分可能性・全微分の定義とその周辺
まずは,2変数関数 f\colon \mathbb{R}^2 \to \mathbb{R} を中心に解説します(定義域は \mathbb{R}^2 全体じゃなくても, A\subset \mathbb{R}^2 を2次元の領域として,その上で考えればよいです)。
全微分の理解には,偏微分の知識が必須ですから,偏微分が分からない場合は,本記事の前に,以下の記事を参照してください。
全微分可能性・全微分の定義
定義(全微分可能性と全微分)
f(x,y) は (a,b)\in \mathbb{R}^2 の近くで定義されている実数値関数とする。
f が (a,b) で全微分可能 (totally differentiable) であるとは,ある A,B\in\mathbb{R} が存在して,絶対値が十分小さい h,k に対し,
かつ \color{red}\displaystyle \lim_{(h,k)\to (0,0) } \varepsilon (h,k)=0 とできることをいう。
f が全微分可能であるとき,(形式的に)
\color{red} df = f_x(a,b)dx+ f_y(a,b) dy
と表し,これを f の (a,b) における 全微分 (total derivative) という。
全微分可能の定義を,ランダウの記号を用いて表すと,
\begin{aligned} &f(a+h,b+k)-f(a,b) \\ &= Ah+Bk+o(\sqrt{h^2+k^2})\quad ((h,k)\to 0) \end{aligned}
となります。あるいは,全微分可能であるとは,ある A, B\in\mathbb{R}^2 が存在して,
とできる,と言っても同じことになります。
なお,後半の「全微分」の定義にあたっては,偏微分を用いていますが,これは以下が成立するからです。
全微分可能ならば偏微分可能
定理(全微分可能ならば偏微分可能)
f(x,y) が (a,b) で全微分可能であるとき,この点で偏微分可能,すなわち, f_x(a,b), f_y(a,b) が存在する。さらに,
\color{red} A=f_x(a,b), \quad B=f_y(a,b)
となる(A,B は全微分可能の定義 \text{(def)} 中のもの)。
全微分は偏微分より強い概念であるということですね。
これを用いて,全微分可能性の式 \text{(def)} を書き改めると,
\color{red}\begin{aligned} &f(a+h,b+k)-f(a,b) \\ &= f_x(a,b)h+f_y(a,b)k+\varepsilon(h,k)\sqrt{h^2+k^2} \end{aligned}
となります。
この定理の証明は,全微分可能性の定義式 \text{(def)} の両辺 k=0 としてから h で割って h\to 0 とすることで x に関する偏微分が従い,同様に y に関する偏微分の存在も従います。
なお,逆は一般に従いません。すなわち,偏微分可能であるからと言って,全微分可能であるとは限りません。たとえば, f(x,y)=\begin{cases} 0 & xy=0, \\ 1 & xy\ne 0 \end{cases} は偏微分可能ですが,全微分不可能です。
ただし,偏微分可能性に加えて,条件を少し追加すると,全微分可能であることが分かります。これについては後述しましょう。
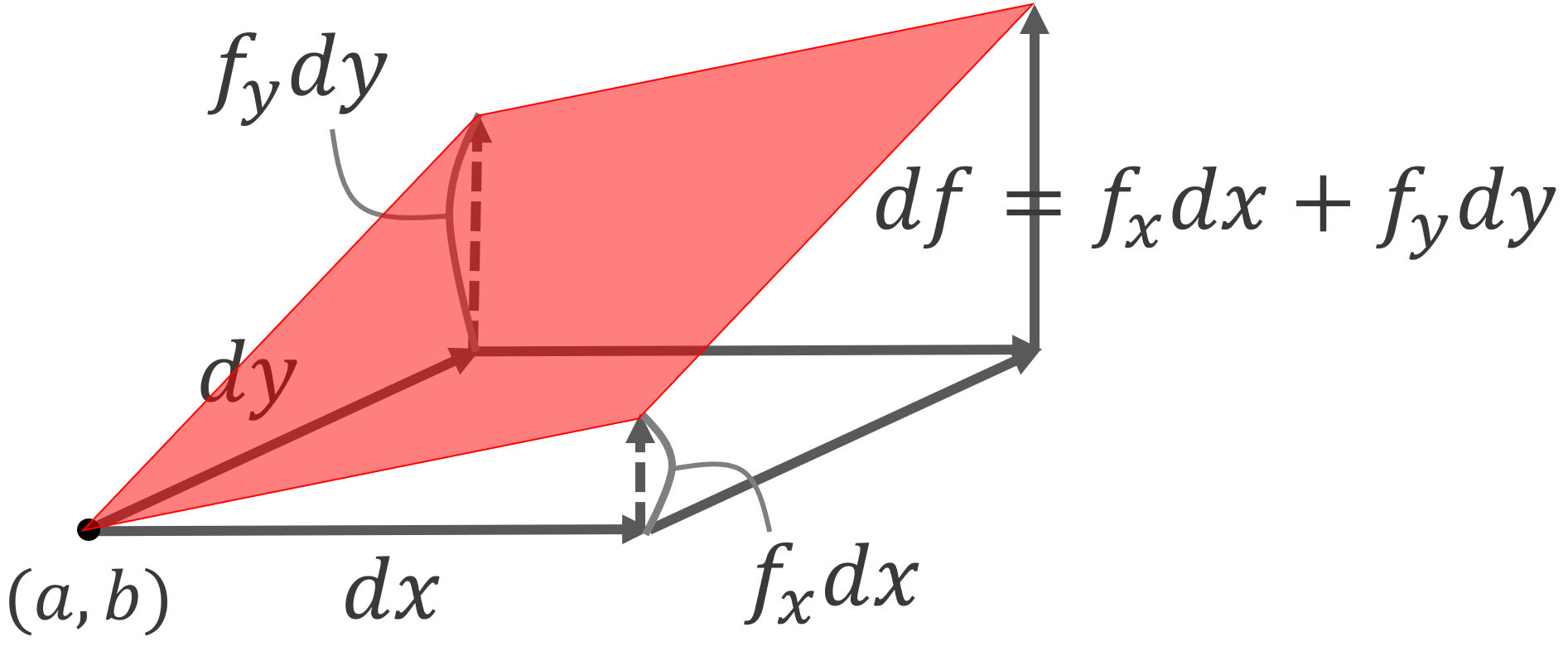
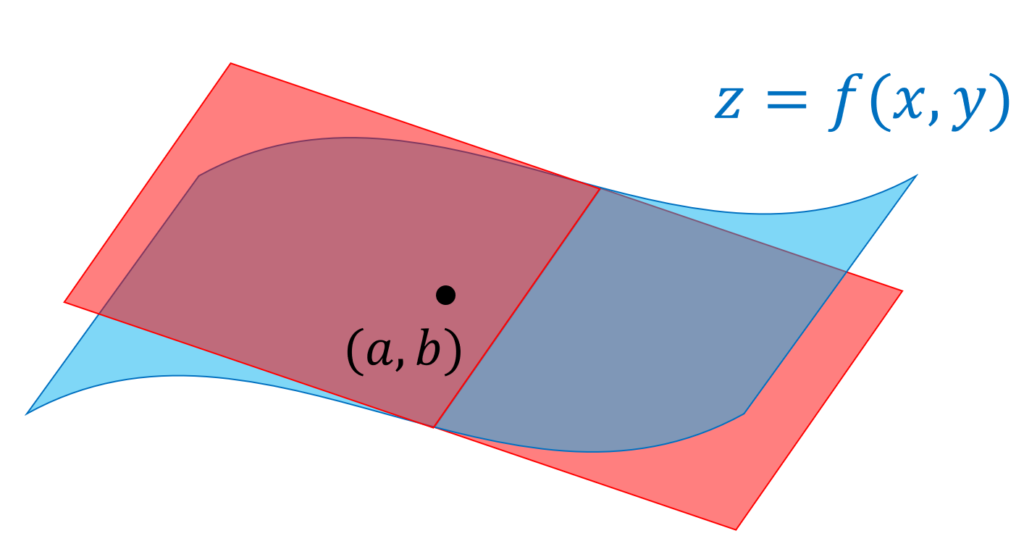
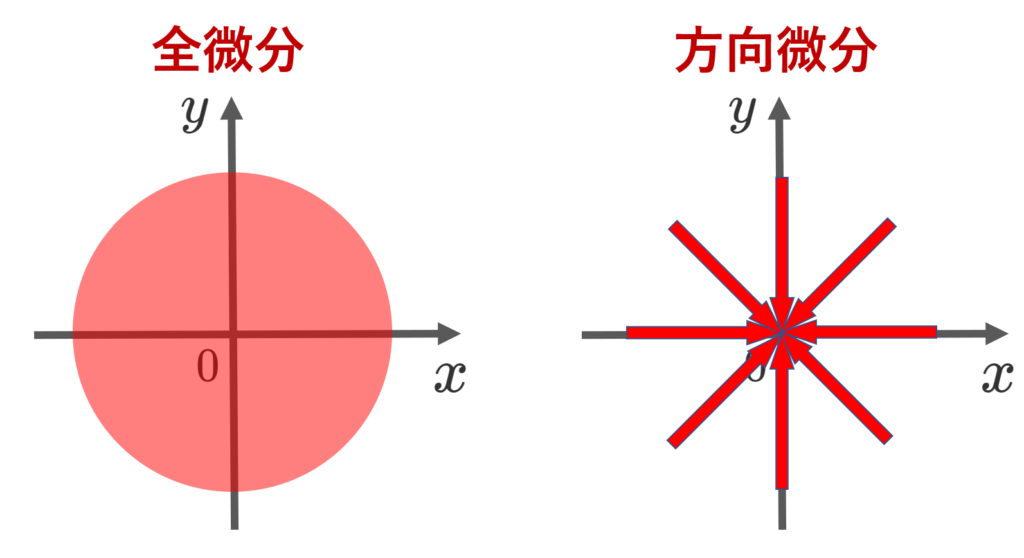
全微分の図形的意味
全微分は, f(x,y) の1次近似を表します。これは,図形的に見ると,接平面を描いていることになります。
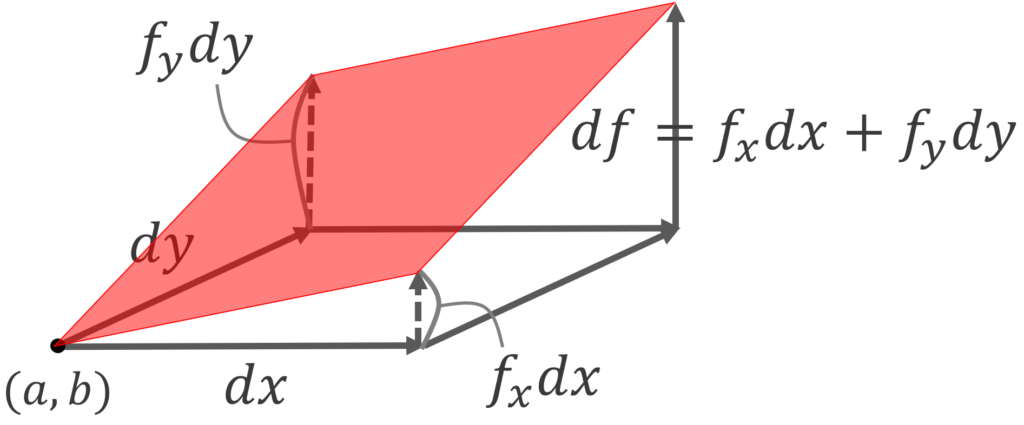
dx, dy, df というのは,微小量を表しています。点 (a,b) から,微小量 (dx, dy) だけ移動すると, f(x,y) の微小変化量 df は,接平面による近似により,おおよそ df = f_x dx + f_ydy になりますよ,とそう言っているのです。
全微分可能・全微分の性質
定義の直後に,「全微分可能であれば偏微分可能」という定理を述べました。それ以外にも,以下のような性質があります。
全微分可能ならば連続
定理(全微分可能ならば連続)
f が (a,b) で全微分可能であれば,この点で連続である。
これの証明は,全微分可能性の定義式 \text{(def)} で両辺 (h,k)\to (0,0) とすることで明らかですね。
注意ですが,偏微分可能なだけでは連続性は従いません。 たとえば, f(x,y)=\begin{cases} 0 & xy=0, \\ 1 & xy\ne 0 \end{cases} は偏微分可能ですが,原点で連続になりません。
偏導関数が連続ならば全微分可能
偏微分可能であるからと言って,全微分可能であることは従いませんが,偏導関数に連続性を課せば,全微分可能になります。全微分可能であることを簡単に確認できる,重要な定理です。
定理(偏導関数が連続ならば全微分可能)
(a,b) の近くで f_x, f_y がともに存在して,そのいずれかが (a,b) で連続ならば,この点で全微分可能である。
特に, f が C^1 級ならば全微分可能である。
C^1 級とは, f_x, f_y が両方存在して両方連続であることを指します(→C1級,Cn級,C∞級関数の定義と具体例5つ)。
ここで, f_x が連続とは, f_x が (a,b) の近くで存在していることを前提としています。
証明を記しておきましょう。
証明
f_x が (a,b) で連続であるとして,全微分可能であることを示す。平均値の定理より,
\begin{aligned} &f(a+h,b+k)-f(a,b) \\ &= (f(a+h,b+k)-f(a,b+k))\\ &\qquad +(f(a,b+k)-f(a,b)) \\ &= hf_x(a+\theta_{h,k}h,b+k) \\ &\qquad +(f(a,b+k)-f(a,b)) \end{aligned}
となる 0\le \theta_{h,k} \le 1 が存在する。ここで,
とおくと, f_x の連続性より, \lim_{(h,k)\to (0,0) }\varepsilon_1(h,k)=0 である。また, f_y の定義より,
とおくと, \lim_{k\to 0}\varepsilon_2(k) =0 である。以上から,
となって,全微分可能である。
証明終
全微分可能であることの確認方法とその具体例
以上の知識も踏まえて,全微分可能であることの確認方法とその具体例をみていきましょう。
全微分可能であることの確認手順
全微分可能であることは,以下の順に確認可能です。
- f が連続であることを確認する → 不連続ならば全微分不可能
- f_x, f_y を計算する → 偏微分不可能なら全微分不可能
- f_x, f_y のいずれかが連続であるかを確認する → 連続ならば全微分可能
- \scriptsize \displaystyle \begin{aligned}&\dfrac{f(x+h,y+k)-f(x,y)-f_x(x,y)h-f_y(x,y)k}{\sqrt{h^2+k^2} }\\ &\xrightarrow{(h,k)\to(0,0)}0 \end{aligned} となるかを調べる → なれば全微分可能,ならなければ全微分不可能
1.と2,3.は手順が逆でも構いません。確認しやすい方から確認しましょう。
1.は,全微分可能ならば連続であるという定理の対偶を取ったものです。
2.は,全微分可能ならば偏微分可能であるという定理の対偶を取ったものです。
3.は偏導関数が連続ならば全微分可能であるという定理を使ったもので,
4.は2.で求めたものを用いて,偏微分可能の定義式 \text{(def)} において,
となることを用いています。実際は,4.を使わねばならない場面はほとんどないでしょう。
なお,方向微分が計算できるのであれば, \nabla_{\boldsymbol{v}} f(\boldsymbol{a})\ne\langle \nabla f(\boldsymbol{a}) , \boldsymbol{v}\rangle であれば全微分不可能であるという判定もできます。ここで,右辺は内積を指し, \small \nabla f(\boldsymbol{a}) = \operatorname{grad} f(\boldsymbol{a})= \left(\frac{\partial f}{\partial x_1}(\boldsymbol{a}),\dots, \frac{\partial f}{\partial x_n}(\boldsymbol{a})\right) です。これについては,方向微分とは~定義・性質・求め方を詳しく~の例題を確認してください。今回は詳しくは述べないことにします。
具体例
簡単な例題を解いてみましょう。
例題1.
f(x,y) = x^3 - y^3 + 2x^2 y は各点で全微分可能か,可能ならば全微分 df を求めよ。
で,これは連続ですから,各点で全微分可能ですね(手順2-3.)。全微分は,
になります。
例題2(全方向微分可能だが,全微分不可能な例).
f(x,y)=\begin{cases} 1 & y=x^2>0 , \\ 0 & \text{otherwise} \end{cases} は原点 (0,0) で全微分可能か,可能ならば全微分 df を求めよ。
y=x^2 に沿って (x,y)\to (0,0) とすると, f(x,y)\to 1 となる一方で, f(0,0)=0 ですから, f は原点で不連続ですね。よって全微分不可能です(手順1.)。
この関数は,任意の方向で方向微分可能ですが,全微分不可能な関数の例になっています。
実際, f_x(0,0)=f_y(0,0)=0 であり,さらに y=rx 方向で切った方向微分も 0 になります。
ちなみに, f_x, f_y は y=x^2>0 上で存在しないため, (0,0) で連続とは言えません。
n変数関数における全微分
最後に,n 変数関数 f\colon \mathbb{R}^n\to \mathbb{R} における全微分を定義しておきましょう。
定義(全微分可能性と全微分)
f(x_1,\dots, x_n) は (a_1,\dots, a_n)\in \mathbb{R}^n の近くで定義されている実数値関数とする。
f が (a_1,\dots a_n) で全微分可能 (totally differentiable) であるとは,ある A_1,\dots, A_n\in\mathbb{R} が存在して,絶対値が十分小さい h_1,\dots, h_n に対し,
と定めると,\color{red}\displaystyle \lim_{(h_1,\dots,h_n)\to (0,\dots, 0) } \varepsilon (h_1, \dots,h_n)=0 となることをいう。
f が全微分可能であるとき,(形式的に)
\color{red} df = \sum_{k=1}^n f_{x_k}(a_1,\dots , a_n)dx_k
と表し,これを f の (a_1, \dots, a_n) における 全微分 (total derivative) という。
このとき,2変数のときと同様に,以下が成立します。
定理(全微分可能ならば偏微分可能)
f(x_1,\dots, x_n) が (a_1,\dots, a_n) で全微分可能であるとき,この点で偏微分可能,すなわち, f_{x_k}(a_1,\dots, a_n) \; (1\le k\le n) が存在する。さらに,
\color{red} A_k=f_{x_k}(a_1,\dots, a_n)\quad (1\le k\le n)
となる(A_k は全微分可能の定義中のもの)。
その他,2変数のときと似たようなことが成立しますが,省略します。