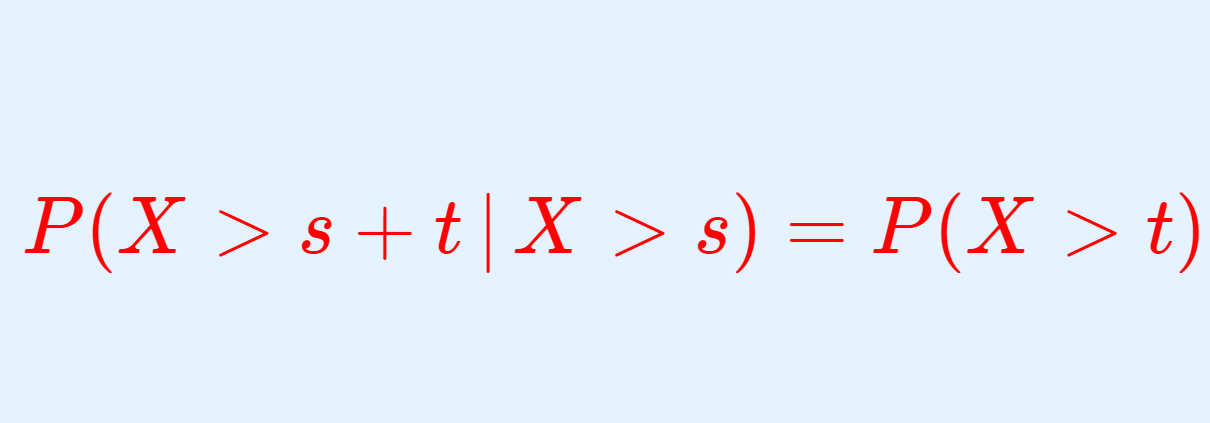指数分布において,無記憶性と呼ばれる P(X>s+t\,|\,X>s) = P(X>t) という性質について解説し,「指数分布が無記憶性をもつ」ことと「連続型確率分布が無記憶性をもつ場合,それは指数分布に限る」ことの2つを証明しましょう。
指数分布の無記憶性
定理(指数分布の無記憶性)
X を指数分布, s, t > 0 とするとき,
\color{red}P(X>s+t\,|\,X>s) = P(X>t)
である。これを,無記憶性 (lack of memory property, memorylessness) という。
逆に,連続型の確率分布において,無記憶性をもつ分布は指数分布に限る。
無記憶性とは,簡単に言うと,前までのことに依存せずに次のことが起こることを意味します。
指数分布とは,「コールセンターに次に電話がかかってくるまでにかかる時間」や「電化製品が次に壊れるまでの時間」などに用いられます。「昨日コールセンターに電話がかかってきたから,今日はかかってこないだろう」とか「昨日電化製品が壊れなかったから,今日は壊れないだろう」とか,そういうことはないわけですから,この事象には,無記憶性があるといえるわけですね。
また,「連続型の確率分布において,無記憶性をもつ分布は指数分布に限る」わけですから,無記憶性をもつ,連続的なモデルを扱いたい場合は,指数分布を用いるのが最も適当であるというわけですね。
指数分布の無記憶性の証明
さて,
- 指数分布が無記憶性をもつこと
- 無記憶性をもつ連続型確率分布が指数分布のみであること
の2つについて,順番に考えていきましょう。
指数分布は無記憶性をもつことの証明
こちらはほぼ明らかですが,証明するとこんな感じです。
証明
\begin{aligned}P(X>s+t\,|\,X>s) &= \frac{P(X>s+t)}{P(X>s)} \\ &= \frac{e^{-\lambda (s+t)}}{e^{-\lambda s}}\\ &= e^{-\lambda t} \\ &= P(X>t) \end{aligned}
より,結論を得る。
証明終
無記憶性をもつ連続型確率分布が指数分布のみであることの証明
さて,逆も考えましょう。こちらは,レベルが上がりますし,少し長くなります。気を引き締めて,丁寧に進めていきましょう。
証明
s,t>0 に対し, P(X>s+t\,|\, X>s) = P(X>t) より,
P(X>s+t) = P(X>s)P(X>t).
G(t) = P(X>t)\,\,(t>0 ) とおくと, G(s+t)=G(s)G(t) である。
これより, n\ge 1 を正の整数とすると,
\begin{aligned} G(n) &= G(n-1)G(1) \\ &=G(n-2)G(1)^2 \\ &=\dots = G(1)^n \end{aligned}がわかる。また,同様に,
G(1)=G\left(n\cdot\frac{1}{n}\right)= G\left(\frac{1}{n}\right)^n
もわかるので, G(1/n) = G(1)^{1/n} を得る。さらに, m, n \ge 1 を正の整数とすると,このことから,
であるから, r\in \mathbb{Q}_{>0} とすると, G(r) = G(1)^r がわかる。
ここで, G(t) = P(X>t) であり,その形から, G は右連続であることに注意する。正の実数 \alpha \in \mathbb{R}_{>0} に対し, \{r_n\} \subset \mathbb{Q_{>\alpha}},\;\, r_n\xrightarrow{n\to\infty} \alpha+ となるような有理数列を取ると,
\begin{aligned}\lim_{n\to\infty} G(\alpha) &= \lim_{n\to\infty} G(r_n) \\ &= \lim_{n\to\infty} G(1)^{r_n}\\ &= \lim_{n\to\infty} G(1)^\alpha \end{aligned}
であるから,結局, G(\alpha) = G(1)^\alpha を得る。従って, \lambda= -\log G(1) とおくと,
となる。 \lim_{\alpha\to\infty} G(\alpha) = \lim_{\alpha\to\infty} P(X>\alpha) = 0 であるから, \lambda > 0 であり,結局,
となって, X \sim \operatorname{Exp}(\lambda) がわかる。
証明終
何とか証明できました。等式 G(x) = G(1)^x を「整数 → 有理数 → 実数」と順番に広げていったわけですね。
なお, f(xy)=f(x)f(y) や, f(x+y) = f(x)+f(y) は,コーシーの等式 (Cauchy’s equation) と呼ばれます。