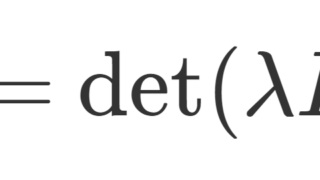A\boldsymbol{x} = \lambda \boldsymbol{x} をみたす複素数 \lambda のことを「固有値」といいます。固有値は \det (\lambda I_n - A) = 0 を解くことで求められます。
本記事では,そんな固有値の求め方(計算手順)について,例題を交えつつ,詳細に解説しましょう。検算方法についても紹介します。
固有値の定義
定義(固有値)
A を n 次正方行列とする。このとき,ある \lambda \in \mathbb{C} と列ベクトル \boldsymbol{x}\in\mathbb{C}^n\setminus\{\boldsymbol{0}\} が存在して,
\color{red} \large A\boldsymbol{x} = \lambda \boldsymbol{x}
となるとき, \lambda を固有値 (eigenvalue) という。
\boldsymbol{x}\mapsto A\boldsymbol{x} という線形変換が, \boldsymbol{x}\mapsto \lambda \boldsymbol{x} という簡単な定数倍でかけるようなものを求めよう,ということですね。固有値はさまざまな研究において登場する,重要な概念です。
なお,このときの \boldsymbol{x} をその固有値に対する固有ベクトル (eigenvector) といいます。固有ベクトルの導出については,本記事では解説せず,固有ベクトル・固有空間の定義・求め方・性質に投げることにします。
本記事では,固有値 \lambda の計算方法を掘り下げます。
固有値の求め方~計算の手順~
さて,固有値 \lambda の求め方を考えましょう。 A を n 次正方行列, I_n を n 次の単位行列とします。
\begin{aligned} A\boldsymbol{x} = \lambda \boldsymbol{x} &\iff \lambda\boldsymbol{x} -A\boldsymbol{x}=\boldsymbol{0}\\ &\iff (\lambda I_n-A)\boldsymbol{x}=\boldsymbol{0}\end{aligned}
ですから,一番最後の式を考えます。 (\lambda I_n -A)\boldsymbol{x}=\boldsymbol{0} となる \boldsymbol{x}\ne \boldsymbol{0} が存在する必要十分条件は,行列 \lambda I_n - A が正則行列(可逆行列)でないこと,すなわち,
となることですから, \det (\lambda I_n -A) = 0 となる \lambda \in \mathbb{C} を求めればよいです。
もちろん,-1 倍した \det (A-\lambda I_n ) = 0 を解いてもよいです。
これが,固有値の求め方です。
ここで,行列式の定義から, \det (\lambda I_n -A ) は \lambda について,n 次の多項式になります(これを固有多項式, \det (\lambda I_n -A)=0 を固有方程式といいます)。よって, n 次正方行列 A の固有値は重複度込みで n 個あります。
以上を一旦まとめておきましょう。
固有値は \det (\lambda I_n -A) = 0 の解 \lambda\in\mathbb{C} である。
固有値は,重複度を込めて n 個ある。
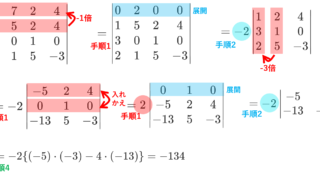
ここで,行列式(det)の定義・計算は,以下のリンク先で別に解説しています。
一応リンク先の内容をまとめておくと,行列式の計算は,
- 行列の基本変形を用いて0を増やす(特に1行目or1列目)
- 1行目or1列目に注目して展開する
- 得られた小さな行列式に対して手順1-2を繰り返す
- 2次・3次または三角行列の行列式に帰着させ,計算する
の順に計算すればよいです。
これを踏まえて,例題に挑戦しましょう。
固有値を求める例題
例題1.
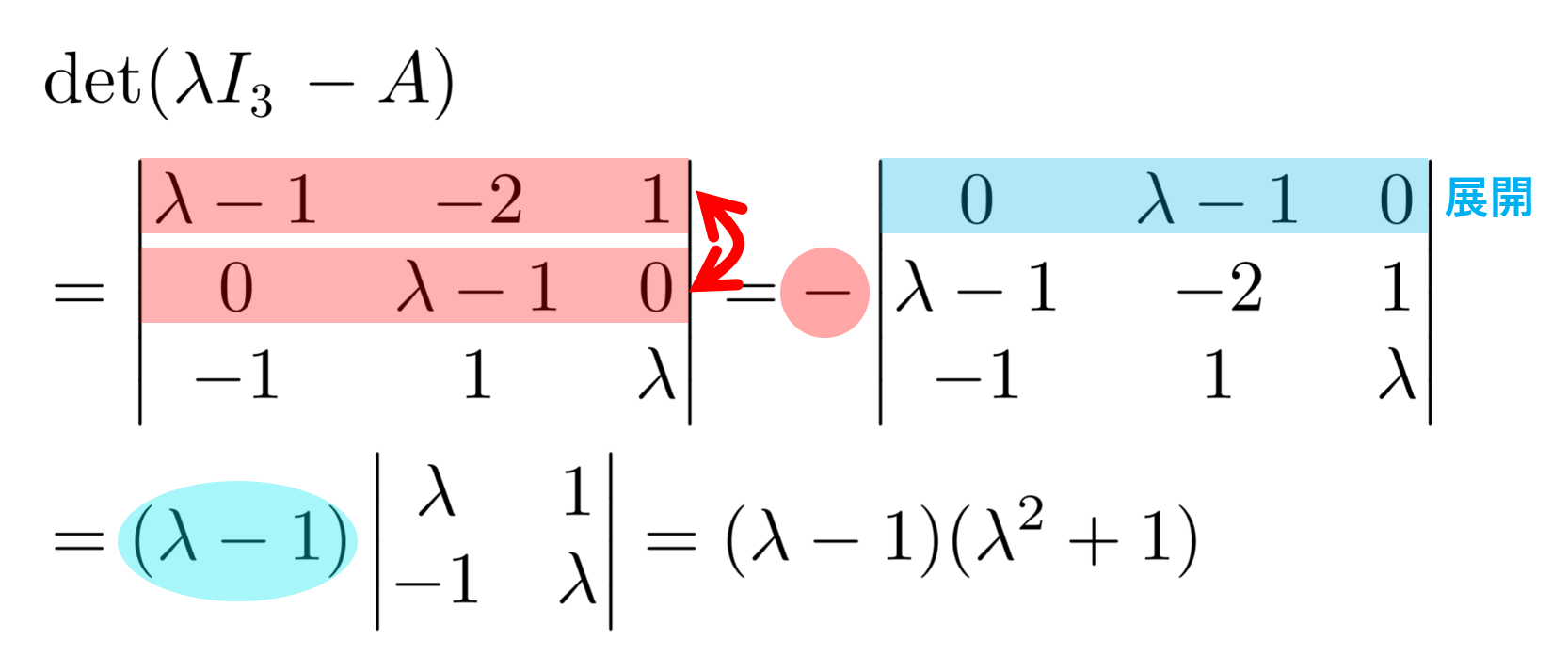
\color{red} A=\begin{pmatrix}0 & 2 & -1 \\ 0 & 1 & 0 \\ 1 & -1 & 0\end{pmatrix} の固有値を全て求めよ。
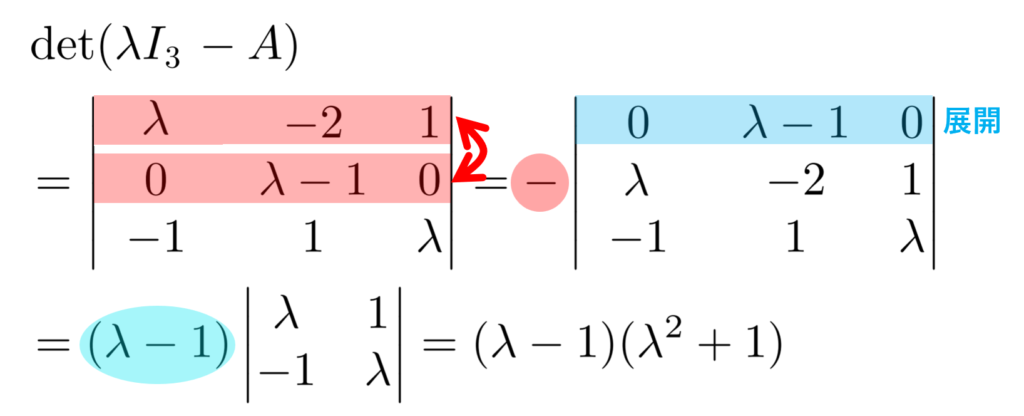
より, \det (\lambda I_3 -A) =0 を解くことで,固有値は \color{red} 1, i,-i となります。
例題2.
\color{red} B=\begin{pmatrix}1 & -1& 0 \\ 0 & 1 & 0 \\ 0 & 2 & -1\end{pmatrix} の固有値を全て求めよ。
例題1の行列の,第1行と第3行を入れ替えただけですが,固有値は変わります。計算してみましょう。
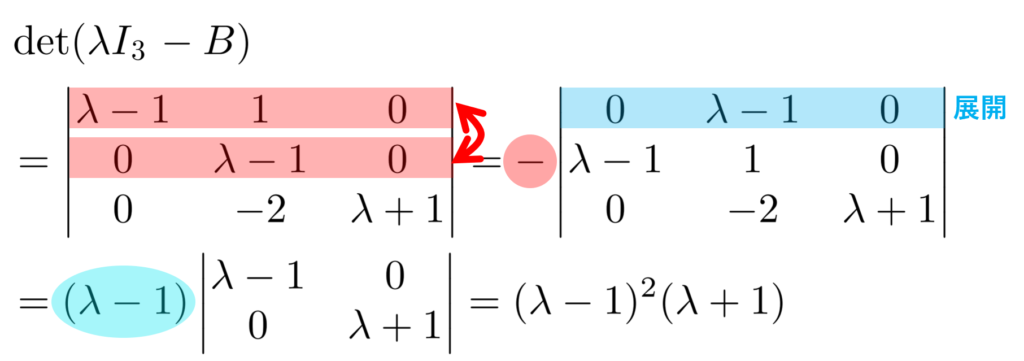
より, \det (\lambda I_3 -B) =0 を解くと, 固有値は \color{red} -1,1 になりますね。 1 の重複度が 2 です。
例題3.
\color{red}C= \begin{pmatrix}1 & 2& -3 \\ 1 & 2 & -3 \\ 1 & 2 & -3\end{pmatrix} の固有値を全て求めよ。
ちょっと変な行列ですが,定義通りに求めましょう。
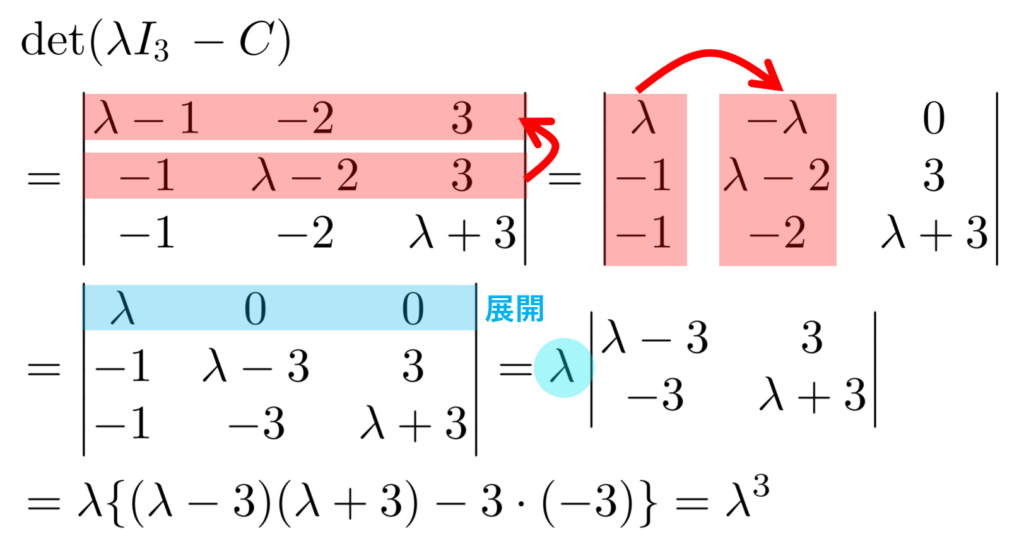
より, \det (\lambda I_3 -C) =0 を解くと, 固有値は \color{red} 0 となりますね。この固有値の重複度は 3 です。
今回は,全ての固有値が 0 になりましたが,「行が一致している行列の固有値は全て 0」とは限らないので注意しましょう。ただし,「行が一致している行列の固有値の少なくとも一つは 0」は正しいです。次の「検算」で解説します。
固有値の検算・性質
求めた固有値の検算に使える性質を述べましょう。
固有値とトレース
定理(固有値とトレース)
A=(a_{ij}) を n 次正方行列,その固有値を(重複度も考えて) \lambda_1,\lambda_2,\dots, \lambda_n とする。このとき,
\color{red} a_{11} + a_{22}+\cdots + a_{nn} = \lambda_1+\lambda_2+\cdots +\lambda_n
が成り立つ。
ここで,左辺は対角成分の和で,トレース (trace) といい, \operatorname{tr} A とかきます。定理の証明は,固有多項式の n-1 次の項に着目すればできますが,詳しくは行列のトレース(tr)とは~定義と性質とその証明~で紹介しています。
対角成分の和と,固有値の和を比較するだけですから,検算に使えそうですね。
固有値と行列式
他に,固有多項式 \det (\lambda I_n -A) = (\lambda-\lambda_1)\dots (\lambda-\lambda_n) の両辺に \lambda=0 を代入して比較することで,次の定理を得ます。
定理(固有値と行列式)
A を n 次正方行列,その固有値を(重複度も考えて) \lambda_1,\lambda_2,\dots, \lambda_n とする。このとき,
\color{red} \det A = \lambda_1\lambda_2\dots\lambda_n
が成立する。
固有値の積が行列式に相当するわけですね。
これを直接検算に使うのは難しい,と思うかもしれません。しかし, A が明らかに正則行列(可逆行列)でないときはどうでしょうか。
このときは \det A= 0 ですから,固有値の積が 0,すなわち,少なくとも一つの固有値は 0 であると分かりますね。
これは,例題3のような場合に,検算に使えそうです。
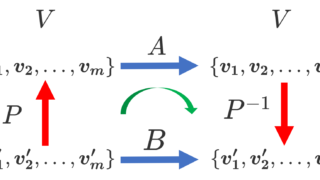
相似な行列の固有値は等しい
正方行列 A,B が相似であるとしましょう。すなわち,正則行列(可逆行列) P が存在して, B=P^{-1}AP であるとしましょう。
このとき,A,B の固有値は等しいことが知られています。これについては,以下の記事で証明しています。
特殊な行列の固有値
最後に,特殊な行列の固有値について,簡単に触れておきましょう。
- 三角行列(上三角行列・下三角行列)の固有値は,その対角成分である。
- エルミート行列の固有値は,全て実数である。
- 実対称行列の固有値は,全て実数である。
- 歪エルミート行列の固有値は,全て純虚数(0を含む)である。
- 実交代行列の固有値は,全て純虚数(0を含む)である。
- ユニタリ行列の固有値は,全て複素平面における単位円上にある。
- 実直交行列の固有値は,全て複素平面における単位円上にある。
解説は各リンク先にあります。
固有ベクトルの求め方
本記事で解説した各例題における,固有ベクトルの求め方は以下で解説しています。
おわりに
実際は,固有値の計算をするのは,線形代数のテストや院試のときくらいでしょう。
普段は,コンピュータやインターネット上でさまざまな計算ができるWolframAlphaなどを用いて計算するとよいです。