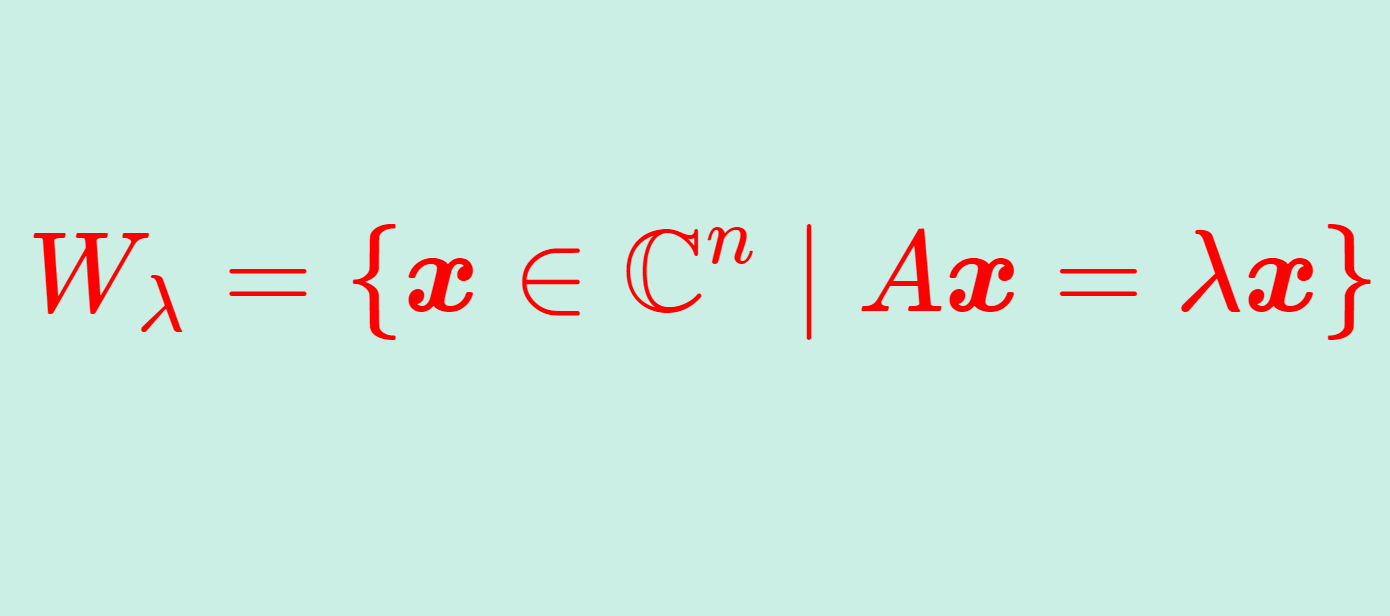A\boldsymbol{x}=\lambda \boldsymbol{x} をみたす \boldsymbol{x} を固有ベクトルといい,その集合を固有空間と良います。
これについて,その定義を述べてから,求め方を具体例を含め解説し,最後に性質を述べましょう。
固有ベクトル・固有空間の定義
定義(固有ベクトル)
A を n 次正方行列とする。このとき,ある \lambda \in \mathbb{C} と列ベクトル \boldsymbol{x}\in\mathbb{C}^n\setminus\{\boldsymbol{0}\} が存在して,
\color{red} \large A\boldsymbol{x} = \lambda \boldsymbol{x}
となるとき, \lambda を固有値 (eigenvalue),\color{red} \boldsymbol{x} をその固有値に対応する固有ベクトル (eigenvector) という。特に( \boldsymbol{0} と,) \lambda に対応する固有ベクトル \boldsymbol{x} の集合
を固有空間 (eigenspace) という。
固有空間は自明でない ( \{\boldsymbol{0}\} でない) ベクトル空間になります。固有空間は連立一次方程式 (\lambda I_n - A)\boldsymbol{x}=0 の解空間ですから,ベクトル空間です(→連立一次方程式の基本解・特殊解と解空間の性質)。
なお,固有ベクトルは,固有値を求めてから求めます。行列 A の固有値は,固有方程式 \det(\lambda I_n-A) =0 の解 \lambda \in \mathbb{C} を求めることで求めます。ただし,I_n は n 次単位行列を指します。固有値の個数は,重複度込みで n 個あります。
固有値の求め方は別に以下で解説しています。
固有ベクトル・固有空間の求め方とその具体例
固有ベクトル・固有空間の求め方を,具体例を通して考えましょう。繰り返しますが,固有ベクトル・固有空間は固有値を求めないとわかりませんから,それについては上のリンク先を参照してください。
その上で,固有ベクトル・固有空間については,連立一次方程式 (\lambda I_n-A)\boldsymbol{x}=\boldsymbol{0} を解けばよいです。連立一次方程式は素直に解いても良いですし,以下で解説した,ガウスの消去法(掃き出し法)を用いてもよいでしょう。
固有空間の \boldsymbol{0} を除くすべての元が固有ベクトルですから,固有ベクトルとして,固有空間の基底を求めることにしましょう。
なお,本サイトでは \mathbb{R}^n でなく, \mathbb{C}^n 上で考えます。
例題1.
A=\begin{pmatrix}0 & 2 & -1 \\ 0 & 1 & 0 \\ 1 & -1 & 0\end{pmatrix} の固有空間とその基底となる固有ベクトル一組を求めよ。
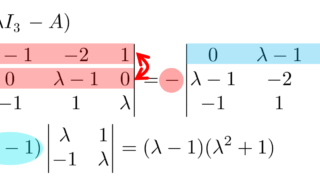
\det (\lambda I_3-A)=(\lambda-1)(\lambda^2+1) ですから,固有値は 1, i,-i です(固有値の定義と求め方をていねいに~計算の手順~の例題1を参照)。各固有値の固有ベクトルを考えましょう。
固有値 1 に対応する固有空間 W_{1} について行基本変形により,
\begin{aligned}&(\lambda I_3 -A)\boldsymbol{x} =\boldsymbol{0} \\ &\iff \begin{pmatrix}1&-2&1 \\ 0&0&0 \\-1 & 1 &1\end{pmatrix}\boldsymbol{x}=\boldsymbol{0}\\ &\iff \begin{pmatrix} 1&0&-3\\0&0&0 \\ 0&-1&2 \end{pmatrix} \boldsymbol{x}=\boldsymbol{0}\\ \end{aligned}
より,求めるべきは \begin{cases} x_1-3x_3=0\\ -x_2+2x_3=0\end{cases} の解で, x_3=a とすることで,
であり,この基底となる固有ベクトルは \color{red}\begin{pmatrix} 3\\2\\1\end{pmatrix} ですね。
同様に計算すると, W_{i}, W_{-i} の基底となる固有ベクトルはそれぞれ \color{red} \begin{pmatrix} i \\ 0 \\1 \end{pmatrix}, \begin{pmatrix} -i\\ 0\\ 1\end{pmatrix} になります。
例題2.
B=\begin{pmatrix}1 & -1& 0 \\ 0 & 1 & 0 \\ 0 & 2 & -1\end{pmatrix} の固有空間とその基底となる固有ベクトル一組を求めよ。
\det (\lambda I_3-B) = (\lambda-1)^2(\lambda+1) より,固有値は 1,-1 ですね(固有値の定義と求め方をていねいに~計算の手順~の例題2を参照)。これから固有値を求めましょう。
固有値 1 に対応する固有空間 W_1 は連立一次方程式 (I_3- B)\boldsymbol{x}=\boldsymbol{0} の解,すなわち
\begin{cases} x_2=0 \\ -2x_2+2x_3=0 \end{cases}
の解ですから,x_2=x_3=0 なので,
ですね。基底となる固有ベクトルは \color{red}\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} で,特に \dim V_1 = 1 です。
また,固有値 -1 に対応する固有空間 W_{-1} は連立一次方程式 (-I_3-B)\boldsymbol{x}=\boldsymbol{0} の解,すなわち
\begin{cases} -2x_1+x_2 = 0\\ -2x_2=0\end{cases}
の解ですから, x_1=x_2=0 なので,
ですね。基底となる固有ベクトルは \color{red} \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} で,特に \dim V_{-1} = 1 です。
例題3.
C= \begin{pmatrix}1 & 2& -3 \\ 1 & 2 & -3 \\ 1 & 2 & -3\end{pmatrix} の固有空間とその基底となる固有ベクトル一組を求めよ。
\det(\lambda I_3-C) =\lambda^3 ですから,固有値は 0 です(固有値の定義と求め方をていねいに~計算の手順~の例題1を参照)。よって固有空間は, C\boldsymbol{x}=\boldsymbol{0} の解集合で
\color{red}W_0 = \left\{ \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}\in\mathbb{C}^3 \middle| x_1+2x_2-3x_3=0\right\}
ですね。基底については, x_1=a,\; x_2=b とおくと, x_3 = (a+2b)/3 であり,
とかけますから,基底の一組は \begin{pmatrix} 1\\0 \\ 1/3 \end{pmatrix}, \begin{pmatrix} 0\\1 \\ 2/3 \end{pmatrix} ですね。あるいは定数倍して, \color{red}\begin{pmatrix} 3\\0 \\ 1 \end{pmatrix}, \begin{pmatrix} 0\\3\\ 2 \end{pmatrix} でもよいです。
固有ベクトル・固有空間の性質
固有ベクトル・固有空間に関する最も基本的な性質を挙げておきましょう。
定理(固有ベクトル・固有空間の性質)
A を n 次正方行列とする。
- A が固有値 \lambda を持つとき, \dim W_\lambda =\dim \operatorname{Ker}(\lambda I_n-A)= n-\operatorname{rank} (\lambda I_n-A).
- A が異なる固有値 \lambda_1 , \lambda_2 を持つとすると, W_{\lambda_1}\cap W_{\lambda_2}=\{\boldsymbol{0}\}.
1.は次元等式です。一般に,斉次連立一次方程式 A\boldsymbol{x}=\boldsymbol{0} の解空間 W は \dim W = \dim \operatorname{Ker} A = n-\operatorname{rank} A です(→連立一次方程式の基本解・特殊解と解空間の性質)。
2.は \boldsymbol{x}\in W_{\lambda_1}\cap W_{\lambda_2} と仮定すると, \lambda_1\boldsymbol{x}=A\boldsymbol{x}=\lambda_2\boldsymbol{x} ですから, (\lambda_1-\lambda_2)\boldsymbol{x}=\boldsymbol{0},すなわち \boldsymbol{x}=\boldsymbol{0} ですね。