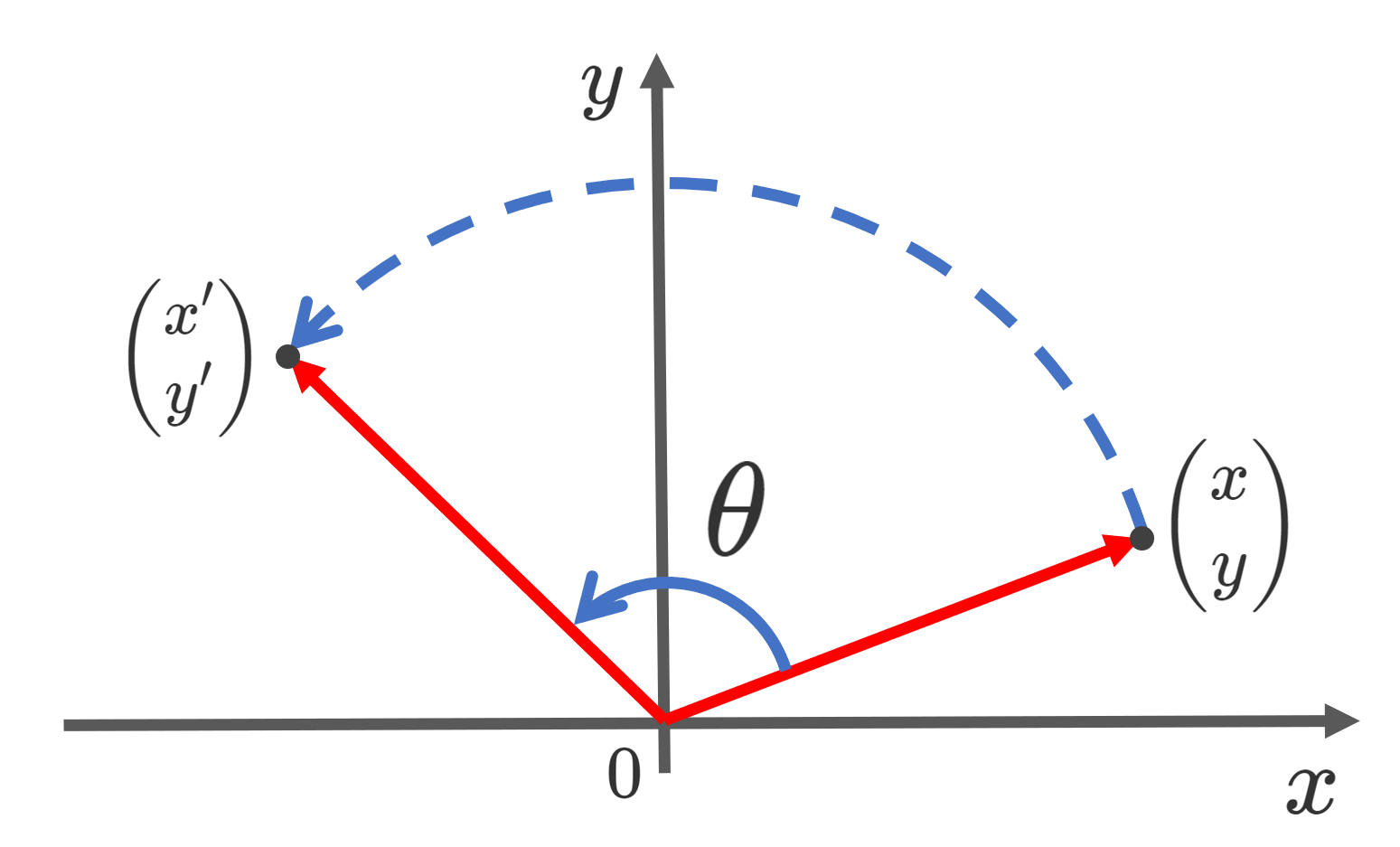
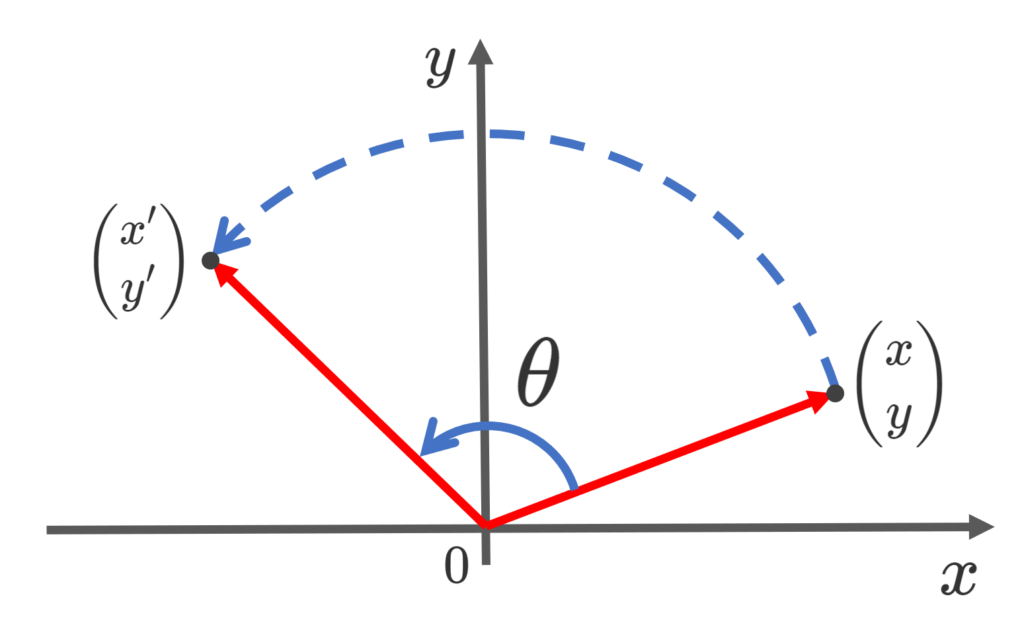
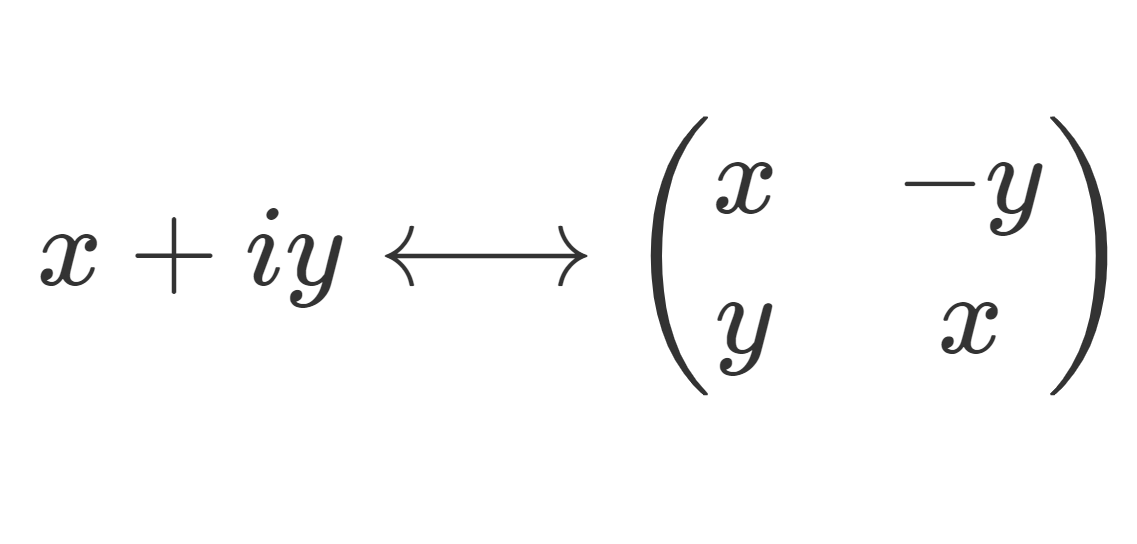\mathbb{R}^2 上の点 \begin{pmatrix} x \\ y\end{pmatrix} について,それを原点を中心に反時計回りに \theta だけ回転させた点を \begin{pmatrix} x' \\ y' \end{pmatrix} とすると,
\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix}\cos \theta & -\sin \theta \\ \sin \theta & \cos\theta \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}
となります。このときの R_\theta = \begin{pmatrix}\cos \theta & -\sin \theta \\ \sin \theta & \cos\theta \end{pmatrix} を回転行列といいます。
この行列について,定義と求め方・性質をわかりやすく解説します。
回転行列の定義
定義(回転行列; rotation matrix)
\color{red} R_\theta = \begin{pmatrix}\cos \theta & -\sin \theta \\ \sin \theta & \cos\theta \end{pmatrix}
を回転行列 (rotation matrix) という。このとき, \begin{pmatrix} x \\ y\end{pmatrix}\in \mathbb{R}^2 を原点中心に反時計回り \theta だけ回転した点の座標は
となる。
行列の積を考えると, \begin{pmatrix}\cos \theta & -\sin \theta \\ \sin \theta & \cos\theta \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} =\begin{pmatrix} x\cos\theta-y\sin\theta \\ x\sin\theta+y\cos\theta \end{pmatrix} ですから,結局
\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} x\cos\theta-y\sin\theta \\ x\sin\theta+y\cos\theta \end{pmatrix}
になります。
まず,回転行列がちゃんと「回転」になっていることを確認しましょう。 \begin{pmatrix} x \\ y \end{pmatrix} を極座標表示すると, x = r\cos\varphi,\; y =r\sin\varphi となり,三角関数の加法定理を用いると,
\begin{aligned}R_{\theta} \begin{pmatrix} x \\ y \end{pmatrix} &= \begin{pmatrix} r\cos\varphi\cos\theta-r\sin\varphi\sin\theta \\ r\cos\varphi\sin\theta+r\sin\varphi\cos\theta \end{pmatrix} \\ &= \begin{pmatrix} r\cos(\varphi+\theta) \\ r\sin(\varphi+\theta) \end{pmatrix} \end{aligned}
より,ちゃんと「回転」になっていますね。
回転行列の求め方(覚え方)
回転行列を忘れてしまったときは, \begin{pmatrix} 1 \\ 0\end{pmatrix}, \begin{pmatrix} 0 \\ 1\end{pmatrix} の回転を考えることで,復元してあげればよいです。 これらを \theta だけ回転すると,
\small \begin{aligned}\begin{pmatrix} 1\\0\end{pmatrix}&\to \begin{pmatrix} \cos\theta \\ \sin\theta\end{pmatrix}, \\ \begin{pmatrix} 0\\1\end{pmatrix} = \begin{pmatrix} \cos \pi/2\\ \sin\pi/2 \end{pmatrix} &\to \begin{pmatrix} \cos(\pi/2+\theta) \\ \sin(\pi/2+\theta)\end{pmatrix} = \begin{pmatrix}-\sin\theta \\ \cos\theta \end{pmatrix}\end{aligned}
であることに留意して, R_\theta = \begin{pmatrix}a & b \\ c& d \end{pmatrix} に代入すると,
すなわち,
ですから,
と求まりますね。
また,複素数と実行列は a+bi \leftrightarrow \begin{pmatrix}a & -b \\ b& a \end{pmatrix} という対応関係があります(→複素数と行列の対応関係を考えよう)。これを知っていれば,
e^{i\theta}=\cos\theta +i\sin\theta\leftrightarrow \begin{pmatrix}\cos \theta & -\sin \theta \\ \sin \theta & \cos\theta \end{pmatrix} =R_\theta
ですから,回転行列と,複素数における回転が対応関係にあることが分かります。
回転行列の性質
回転行列の基本的かつ重要な性質を挙げましょう。
定理(回転行列の性質)
R_\theta = \begin{pmatrix}\cos \theta & -\sin \theta \\ \sin \theta & \cos\theta \end{pmatrix} とすると,以下が成立する。
証明は,三角関数の加法定理などを用いながら,ひとつずつ丁寧に確認していけば分かるため,省略します。それよりも,イメージを持つことが大切です。
たとえば,2n\pi だけ回転させると,元の位置に戻ってきますから,それは恒等写像に相当する単位行列になります。 (2n+1)\pi 回転させると,元の位置に対して,原点対称な点になりますから,符号が変わって -I になります。
3.について, \alpha+\beta 回転は, \alpha 回転してから \beta 回転したり,あるいは \beta 回転してから \alpha 回転しても同じですから,成立します。
4.については, \theta 回転の「逆」は, -\theta 回転ですから, R_{\theta}^{-1} =R_{-\theta} が成立し,さらに直交行列になることが示せます。直交行列とは,内積を変えない行列です(→直交行列の定義と性質10個とその証明)。
5.については,回転行列によって,ベクトルの大きさは変わらないことを意味します。実際,
\| R_\theta \boldsymbol{v}\| = \|\boldsymbol{v}\|
となることは,イメージから考えて分かるでしょう。
回転行列と線形写像
最後に,回転行列の,線形写像的見方をしておきましょう。
回転による写像 f_\theta は f_\theta \colon \mathbb{R}^2\to \mathbb{R}^2 の線形写像です。その線形写像の基底 \boldsymbol{e_1}=\begin{pmatrix} 1 \\ 0\end{pmatrix}, \; \boldsymbol{e_2}=\begin{pmatrix} 0 \\1 \end{pmatrix} に対する表現行列が R_\theta になっています。実際,
\begin{pmatrix}f_\theta(\boldsymbol{e_1}) & f_{\theta}(\boldsymbol{e_2}) \end{pmatrix}= \begin{pmatrix} \boldsymbol{e_1} & \boldsymbol{e_2} \end{pmatrix}R_\theta
が成立します。