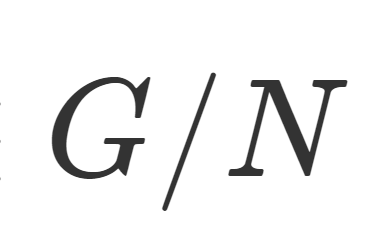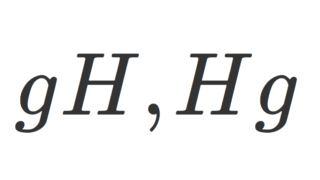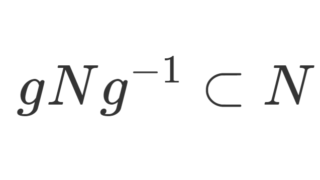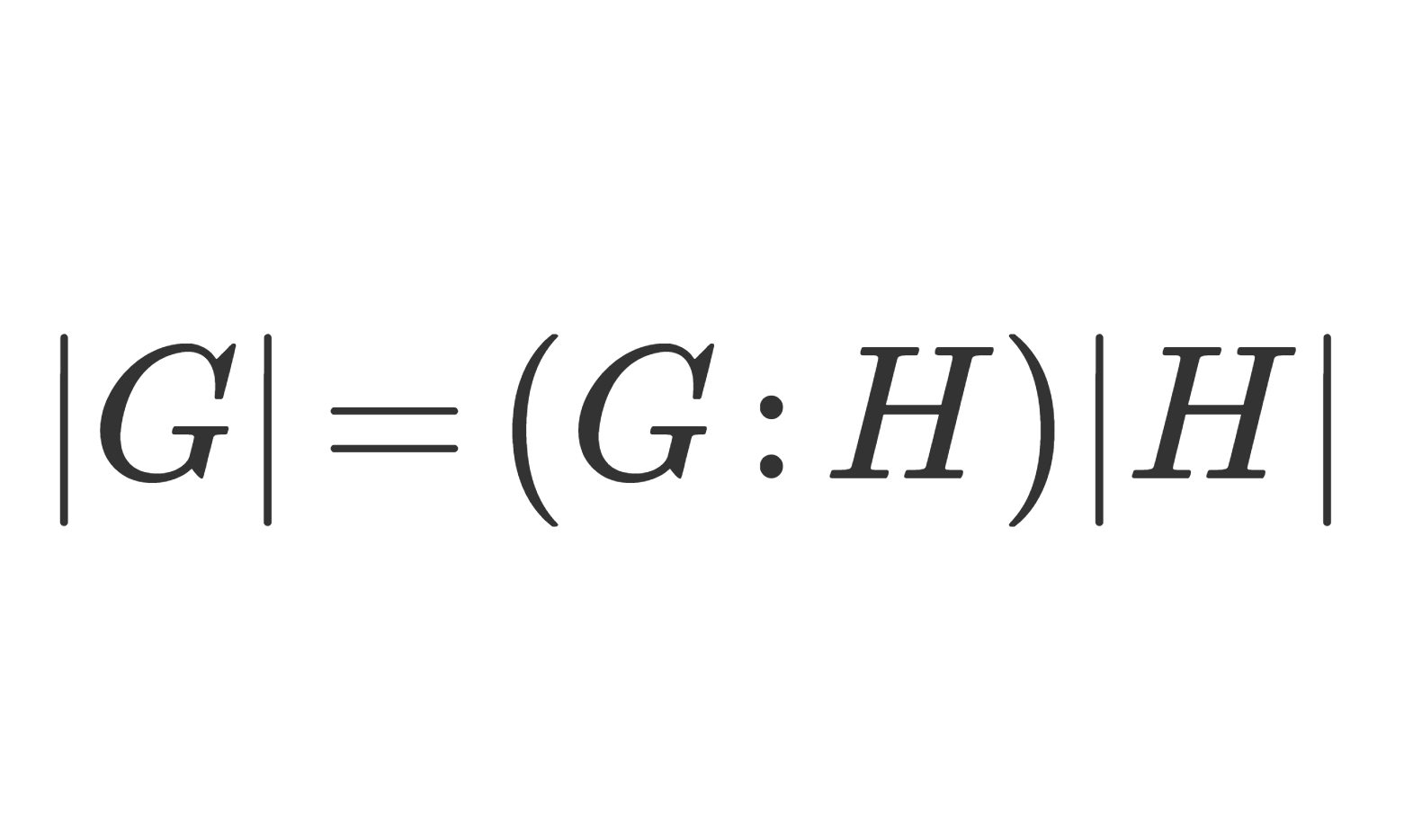剰余群(商群)とは，群の剰余類の商集合に演算を入れて再び「群」と思ったものを指します。意味不明かもしれませんが，順を追って解説していきます。
剰余群(商群)の定義にあたっては，well-defined の概念が非常に大事になってきますから，そこも踏まえてしっかりと理解していきましょう。
剰余群(商群)の定義と「群」であることの証明
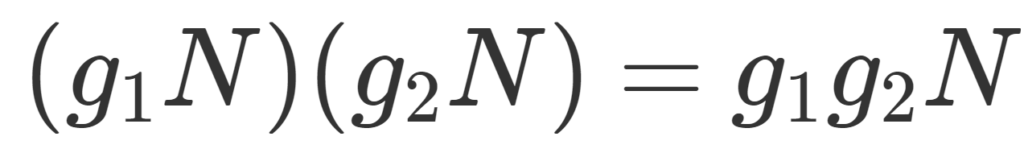
まず最初に定義をかき，それからいくつかの概念について復習を入れた後に，定義が well-defined であること(意味があるということ)を証明しましょう。
剰余群(商群)の定義
とりあえず最初に定義を述べましょう。後で簡単に復習するため，定義の用語は一部分からないものがあっても構いません。
定義1 (剰余群(商群))
G を群， N\subset G を正規部分群とする( N\triangleleft G)。このとき，剰余類の集合 G/N =\{ gN\mid g\in G\} は演算
\color{red}\large (g_1N)(g_2N) = g_1g_2N \in G/N
によって群をなす。このときの G/N を剰余群 (factor group) または商群 (quotient group) という。
g_1g_2N と書きましたが， (g_1g_2)N の意味です。
まずは定義の理解に必要な，「剰余類・剰余集合」と「正規部分群」の概念の簡単な復習を行いましょう。
剰余類と正規部分群の簡単な復習
N\subset G を部分群， g\in G とするとき， gN = \{ gn\mid n\in N\}, \; Ng = \{ng\mid n\in N\} をそれぞれ左剰余類・右剰余類という。 さらに左剰余類全体の集合 G/N = \{ gN\mid g\in G\} を左剰余集合といい，右剰余類全体の集合 N\backslash G = \{ Ng\mid g\in G\} を右剰余集合という。
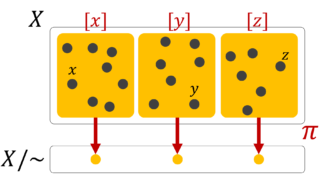
左剰余類・右剰余類は同値類である。すなわち，群 G の元をグループ分け(分割)していることに相当し，
左剰余集合・右剰余集合は同値類で割った商集合，すなわちグループ分けを行った各部分集合を一つの塊(元)とみなした集合である。
G が可換群(アーベル群)のときは，左剰余類と右剰余類は一致し，したがって左剰余集合と右剰余集合は一致します。
剰余類・剰余集合の解説は以下で行っています。
赤字で書いた部分は同値類の考え方で，抑えておくべき考え方です。これについては，以下の記事で図解しています。
N\subset G を部分群とする。任意の g\in G に対して，gNg^{-1}\subset N が成立するとき， N を正規部分群といい， N\triangleleft G とかく。
正規部分群とは， gN = Ng\; (g\in G) が成り立つ部分群，すなわち左剰余類と右剰余類が(集合として)一致している部分群である。特に G/N = N\backslash G である。
G が可換群(アーベル群)のときは，全ての部分群が正規部分群になります。
正規部分群の詳しい解説は，以下を参照してください。
以上の概念を踏まえると，最初の定義は次のように言えます。
N\subset G が正規部分群なら，剰余類 gN=Ng を一つの塊(元)と見た剰余集合 G/N=N\backslash G は，再び積の演算を入れることができて群と思える。
こんな感じです。
剰余群(商群)が「群」となっていることの証明
さて，以上を踏まえて，剰余群(商群)が確かに群となっていることを確認しましょう。示すべきは以下の定理です。
定理2（剰余群は確かに群である）
N\subset G が正規部分群ならば，剰余集合 G/N 上の二項演算
\color{red}\large \begin{equation}(g_1N)(g_2N) = g_1g_2N \in G/N \end{equation}
は well-defined であり，これにより G/N は群をなす。
積の定義 (1) 式は「定義」ですから，左辺が未知の演算（(剰余類) \in G/N 同士の新たな演算）で，右辺が既知のものです。
大事なのは well-defined であることの証明です。示すべきは写像
G/N\times G/N \ni (g_1N, g_2N)\mapsto g_1g_2N \in G/N
が well-defined であること(ちゃんと定義できていること)です。というのも，剰余類の積は各剰余類の代表元（ gN の「代表元」とは g\in G のこと）を用いて定義されています。
しかし同じ剰余類に対し，代表元の取り方は一通りではなく，複数あるため，代表元の取り方に依らずに積演算が定まることを示さねばなりません。そうでないと上が写像にならないからです。具体的には，
を示さねばなりません。
well-defined の概念が専門数学で最初に重要になるのは，ココかもしれません。大事な概念ですから，しっかりと理解してください。
証明
演算の well-definedness について
示すべきは上の (2) 式であった。そこで g_1N = g'_1N ,\; g_2N=g'_2N とする。このとき， n_a, n_b\in N が存在して， g_1n_a=g'_1n_b とできる。特に g'_1 = g_1n_an_b^{-1} であり， n_1=n_an_b^{-1} とおくことで，\color{red} g'_1 = g_1n_1 としてよい。同様に \color{red} g'_2= g_2n_2 となる n_2\in N が存在する。
\begin{aligned} g'_1g'_2 &=g_1n_1g_2n_2 = g_1\textcolor{blue} {g_2g_2^{-1}} n_1g_2n_2 \\ &= g_1 g_2 \textcolor{orange}{(g_2 n_1g_2^{-1})} n_2 \end{aligned}
であり， N は正規部分群であるから， g_2n_1g_2^{-1}\in N である。よって， g'_1g'_2\in g_1g_2 N となるため， g'_1g'_2 N\subset g_1g_2N である。同様に g_1g_2N\subset g'_1g'_2N も言えるので， g_1g_2N=g'_1g'_2N である。
よって (2) 式が示せたので演算は well-defined である。
G/N が群をなすことについて
結合法則は容易に確認可能。
G/N の単位元は N=eN \in G/N (e は G の単位元) となることが容易にわかる。
逆元の存在は， (gN)(g^{-1}N) = gg^{-1} N = N であることから (gN)^{-1} = g^{-1}N である。
証明終
剰余群(商群)の具体例
ちょっと定義の解説が長くなってしまいましたが，やはり具体例を見るのが分かりやすいでしょう。
可換群のときは，群の演算を g_1g_2 ではなく g_1+g_2 のような形でかくことが多いです。
例1.
\mathbb{Z} を和(加法)に関する可換群(アーベル群)と見ると，3の倍数の集合 3\mathbb{Z}\subset\mathbb{Z} は可換群の部分群なので正規部分群である。このとき，
\mathbb{Z}/3\mathbb{Z} = \{ 3\mathbb{Z}, 1+3\mathbb{Z},2+3\mathbb{Z}\}
は
を演算として可換群(アーベル群)になる。
簡単に言うと {}\bmod 3 の世界です。{}\bmod 3 の世界は，和に関して群になります。
例2.
\mathbb{R} を和(加法)に関する可換群(アーベル群)と見ると， 2\pi\mathbb{Z}\subset\mathbb{R} は可換群の部分群なので正規部分群である。このとき，
\mathbb{R}/2\pi \mathbb{Z} = \{ r+2\pi\mathbb{Z}\mid r\in\mathbb{R}\}
は
を演算として可換群(アーベル群)になる。
{}\bmod 2\pi の世界です。考え方は例1.と同じです。
例3.
3 次対称群 S_3 に対して， 3 次交代群 A_3\subset S_3 は正規部分群である。このとき，
S_3/A_3 =\{ A_3, (12)A_3\}
となる(→剰余類と部分群の指数～定義と具体例～)が，これは，
を演算として群となる。特にこれは可換群(アーベル群)である。
これは，元の群は可換群(アーベル群)ではないが，剰余群は可換群(アーベル群)になる例です。
S_3/A_3 の元 \sigma_1 A_3 を \sigma_1 と同一視することで， S_3/A_3 は S_2= \{ e, (12)\} と「群として同じ」と思ったかもしれません。これは「群の同型」という考え方で，準同型定理という群論において非常に重要な考え方に結びつきます。
実際，群として S_3/A_3\simeq S_2\simeq \{\pm 1\} が知られています( \simeq は「同型」の意味)。別の記事で解説しましょう。
剰余群(商群)の基本的な性質
定理3（剰余群(商群)の基本的な性質）
G を群， N\subset G を正規部分群とする( N\triangleleft G)。このとき，
- G が可換群(アーベル群)ならば G/N もそうである。
- G が有限群であるとき，剰余群 G/N の位数(元の個数)について， \displaystyle \color{red} |G/N| = \frac{|G|}{|N|} が成り立つ。
- \pi\colon G\ni g \mapsto gN \in G/N は全射準同型である。これを自然な射影という。 \operatorname{Ker} \pi = N である。
\operatorname{Ker} \pi の定義は \operatorname{Ker} \pi = \{ g\in G\mid \pi(g)=eN\} であることに注意してください。
証明
1. G が可換群(アーベル群)ならば G/N もそうであることについて
明らか。可換のときは，剰余群の演算は (g_1+N)+(g_2+N)=(g_1+g_2)+N とかかれる。
2. |G/N| = \dfrac{|G|}{|N|} について
ラグランジュの定理を言い換えたに過ぎない(→ラグランジュの定理とその証明・応用例【群論】)。
3. \pi \colon G\ni g \mapsto gN \in G/N が全射準同型であり，\operatorname{Ker} \pi =N であることについて
\pi が全射であることは明らか。 g,h\in G について， \pi(gh)=(gh)N =(gN)(hN) = \pi(g)\pi(h) より \pi は準同型である。
G/N の単位元は N なので， \operatorname{Ker}\pi =N である。
証明終
