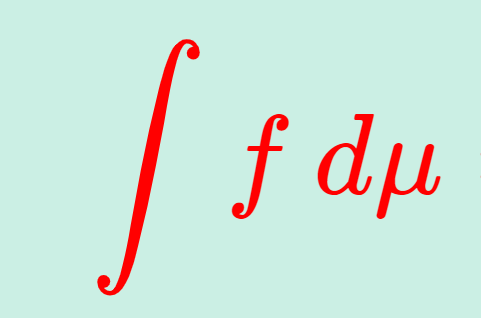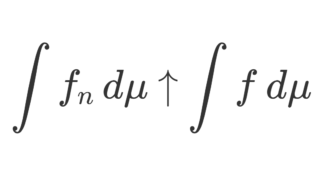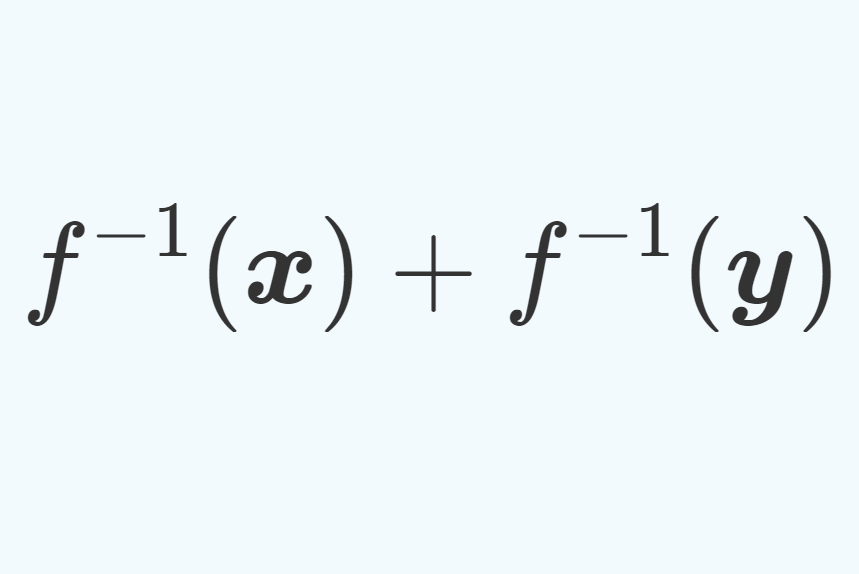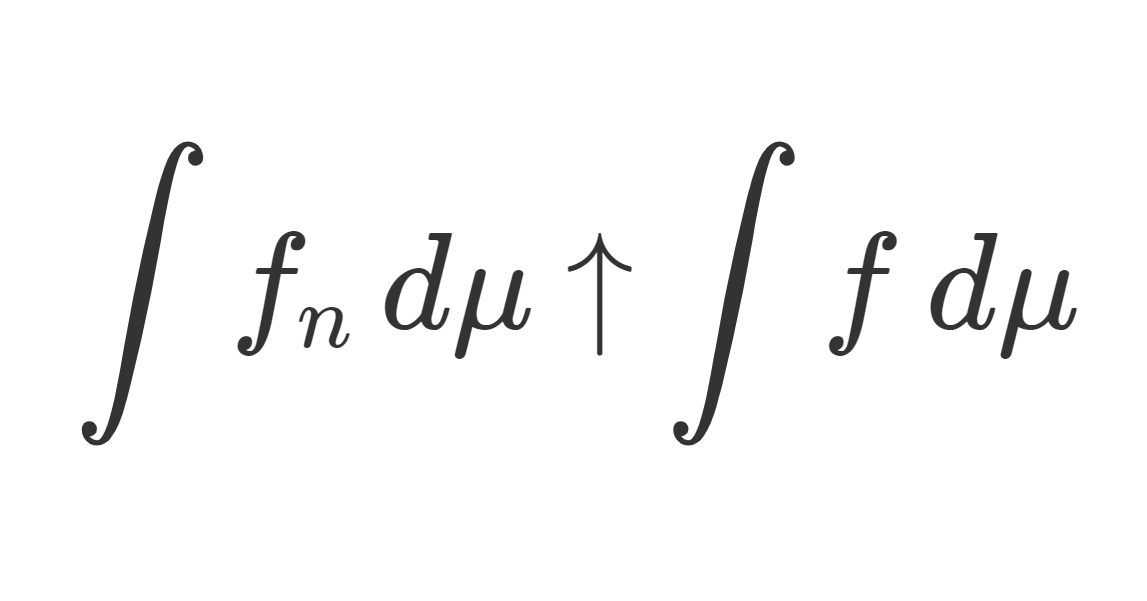数学科向けに,ルベーグ積分の定義を「非負単関数→非負可測関数→一般の可測関数」の順に述べていきましょう。
ルベーグ積分の定義
以下,特に断らない限り (X,\mathcal{F}, \mu) を測度空間とします。
ルベーグ積分 (Lebesgue integral) と言ったときには,一般の測度空間における積分を指すときと,より具体的に測度空間 (\mathbb{R}^d,\mathcal{B}(\mathbb{R}^d),\mu) で, \mu がルベーグ測度になるときの積分を指すときがあります。今回は主に前者の意味で使います。
0. 全ステップの定義を先に軽く紹介
各ステップを解説していく前に,全てのステップの定義を軽く紹介しておきましょう。以下の4ステップからなります。
- f = \sum_{k=1}^n a_k 1_{A_k}\ge 0 (非負単関数)のときに \color{red}\int f\, d\mu = \sum_{k=1}^n a_k \mu(A_k) で定義する。
- f\colon X\to [0,\infty) (非負可測関数)のときに, \color{red}\int f\, d\mu = \sup \left\{ \int g \, d\mu\mid 0\le g\le f:\text{simple}\right\} で定義する(simple は単関数の意味)。
- f \colon X\to \mathbb{R} (可測関数)のときに, f^+ = \max\{ f, 0\},\, f^{-}=\max\{-f, 0\} と関数を正負の部分に分けることで, \color{red}\int f\, d\mu = \int f^+ \,d\mu-\int f^- \, d\mu で定義する。
- A\in\mathcal{F} に対し,\color{red} \int_A f\,d\mu = \int f1_A\, d\mu で定義する。
なお,積分は \int f\, d\mu の代わりに \color{red} \int f(x)\, d\mu(x) や \color{red} \int f(x)\, \mu(dx) というかき方もします。
それでは,具体的に定義を見ていきましょう。
1. 非負単関数におけるルベーグ積分
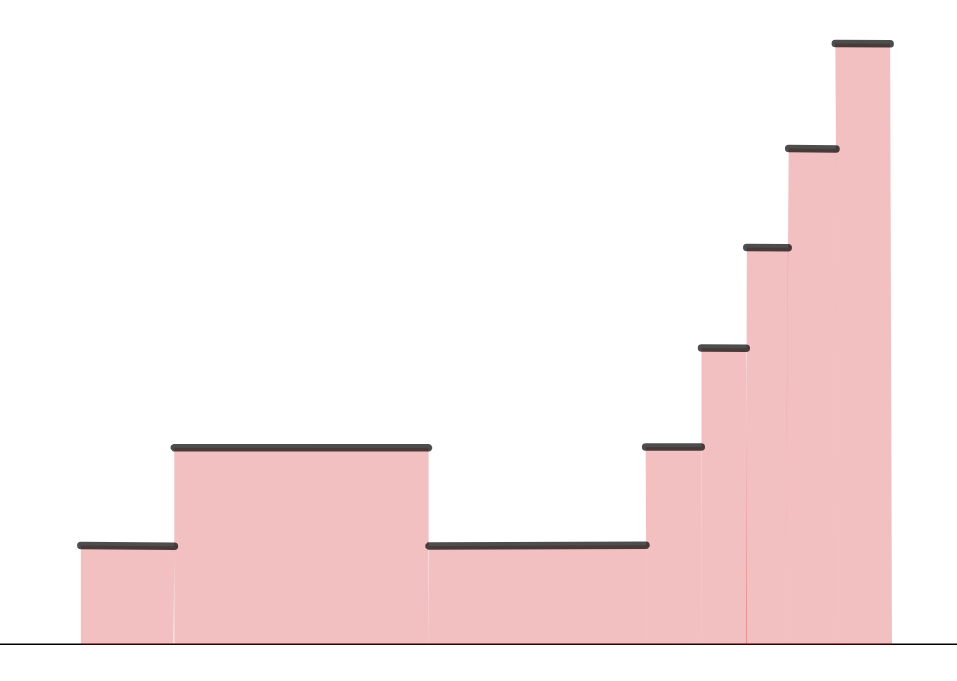
定義1(非負単関数における積分)
非負単関数 \color{red} f(x) =\sum_{k=1}^n a_k 1_{A_k}(x)\; (a_k \in [0,\infty) ,\, A_k\in\mathcal{F}) における積分を
\color{red} \int f\, d\mu = \sum_{k=1}^n a_k \mu(A_k)\in [0,\infty]
と定義する。ただし, 0\cdot \infty =0 とする。
特に, A\in\mathcal{F} に対し, \color{red}\int 1_A \, d\mu = \mu(A) ですね( 1_A は定義関数)。積分値は無限になっても構いません。
最後の注意は, a_k=0,\, \mu(A_k)=\infty だった場合の積の解釈です。なお, a_k=\infty の場合もこの積分は定義可能です。
以下の定理は,上の定義が well-defined であることを保証しています。
定理1(積分の値は単関数の表示方法によらない)
非負単関数 f(x)= \sum_{k=1}^m a_k 1_{A_k}(x)\; (a_k \in [0,\infty) ,\, A_k\in\mathcal{F}), g(x)= \sum_{k=1}^n b_k 1_{B_k}(x)\; (b_k \in [0,\infty) ,\, B_k\in\mathcal{F}) が f=g ならば,
\int f\, d\mu = \int g\, d\mu
が成り立つ。すなわち非負単関数が2通りの表示を持てば,積分の値が一致する。
ここで,たとえば A_i \cap A_j \neq \emptyset であっても構いません(定義も実はそうでした)。
証明は, \{A_n\},\{B_n\} の両方の細分になるような,各元が互いに素な集合族 \mathcal{D} を取ります。
証明
示すべきことは \sum_{k=1}^m a_k 1_{A_k}= \sum_{k=1}^n b_k 1_{B_k} ならば \sum_{k=1}^m a_k \mu({A_k})= \sum_{k=1}^n b_k \mu({B_k}) となることである。
\mathcal{D}\!=\!\left\{ \!\!\left(\bigcap_{k=1}^m A'_k\right) \!\cap \! \left(\bigcap_{k=1}^n B'_k\right) \!\!\colon \!\!\begin{gathered}A'_k = A_k \text{ or } A_k^c \\ B'_k = B_k \text{ or } B_k^c \end{gathered}\right\}
と定めると,これは \mathcal{D}\subset \mathcal{F} であり,\mathcal{D} のどの元も互いに素(共通部分を持たない)である。
\mathcal{D} = \{D_1, D_2, \dots, D_r\} とおく。各 k,i に対して, A_k \cap D_i = D_i \text{ or } \emptyset なので, D_i 上で関数の値は一定である。その値を c_i とすることにする。このとき,
\begin{aligned}\sum_{k=1}^m a_k \mu({A_k}) &= \sum_{k=1}^m a_k \sum_{i=1}^r \mu(A_k\cap D_i) \\ &= \sum_{k=1}^m a_k \sum_{i=1}^r \mu( D_i)1_{\{A_k\cap D_i=D_i\}} \\ &= \sum_{i=1}^r \mu( D_i)\sum_{k=1}^m a_k1_{\{A_k\cap D_i=D_i\}} \\ &= \sum_{i=1}^r c_i \mu(D_i). \end{aligned}
同様に \sum_{k=1}^n b_k\mu(B_k) = \sum_{i=1}^r c_i \mu(D_i) もわかる。
証明終
なお定理1は f=g が各点で成り立っていなくても, f=g, \; \mu\text{-a.e.} (ほとんどいたるところ)でも成立します。実際, f=\sum_{k=1}^n a_k 1_{A_k} = \sum_{k=1}^n a_k 1_{A_k\cap \{ f=g\}} + \sum_{k=1}^n a_k 1_{A_k\cap \{ f\ne g\}} と, \mu(A_k \cap \{ f=g\} )=\mu(A_k),\; \mu(A_k \cap\{ f\ne g\})=0 から従います。
また,同様の証明( D_i 上の値を c_i\le c'_i にすること)により,非負単関数 f,g に対し,
\begin{equation} f\le g \implies \int f\,d\mu \le \int g\,d\mu \end{equation}
が成り立ちます。
2. 非負可測関数におけるルベーグ積分
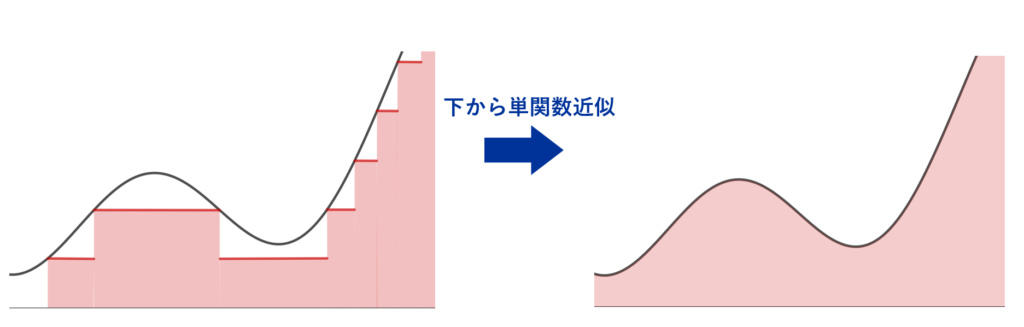
定義2(非負可測関数における積分)
非負可測関数 \color{red} f\colon X\to [0,\infty) における積分を
\color{red}\!\!\!\begin{aligned} \int f\, d\mu= \sup \left\{ \int g\, d\mu\, \middle| \,0\le g\le f : \text{simple}\right\}\end{aligned}
で定義する。simpleとは単関数の意味である。
非負可測関数の積分は,単関数を下から近似することで定義するんですね。リーマン積分のときは上下両方から長方形近似しましたが,単に下から近似する形で定義することで,リーマン積分より扱いやすいわけです。
非負可測関数は f\colon X\to [0,\infty] のように,無限大値を許しても構いません。
f が非負単関数のとき,定義2が定義1に一致していることは, (1) 式からわかります。
このとき, f_n \uparrow f となる単関数列 \{f_n\} を一つ取れば,積分の値が求められることが知られています。以下の定理です。
定理2(単関数近似による非負可測関数の積分)
f は非負可測関数,\{f_n\} は非負単関数の列で,各点で f_n \uparrow f とする。このとき,
\lim_{n\to\infty} \int f_n\, d\mu = \int f\,d\mu
が成り立つ。
f_n \uparrow f とは,各点 x\in X で f_1(x)\le f_2(x)\le f_3(x)\le \dots かつ f_n(x)\to f(x) を指します。
なお,任意の非負可測関数は,単関数で下から近似できることが知られています(→単関数とは何か~定義と可測関数の単関数近似~)。したがって,どんな可測関数 f\ge 0 でも,定理のような列 \{f_n\} は必ず取ってくることが可能です。
証明
\int f_n \, d\mu は広義単調増加であるから極限は存在する。また,定義より
\begin{equation}\lim_{n\to\infty} \int f_n \,d\mu \le \int f\,d\mu\end{equation}
である。
まず,f が非負単関数のときに定理を示す。
f = \sum_{k=1}^m a_k 1_{A_k} とする。ただし, \{a_k\}\subset (0,\infty),\;\{ A_k\}\subset\mathcal{F} とし, \{A_k\} はどの2つも互いに素(共通部分を持たない)とする(これが可能であることは単関数とは何か~定義と可測関数の単関数近似~で解説している)。 n,m,k\in\mathbb{Z}_{\ge 1} とし,
B_{n, m,k} = A_k \cap \left\{ f_n > a_k -\frac{1}{m}\right\}
と定める。 A_k 上 f_n\uparrow_n a_k であるから, B_{n,m,k}\uparrow_n A_k である。よって, \mu(B_{n,m,k})\uparrow_n \mu(A_k) である(測度の性質)。ゆえに,
上で,k についての和は有限和であることに注意する。m\to\infty とすることで,
(2),(3) 式より,示せた。
次に,一般の非負可測関数 f について示す。
\sup の定義より,ある非負単関数の列 \{g_n\} が存在して, g_n \le f かつ \lim_{n\to\infty} \int g_n \, d\mu = \int f\, d\mu とできる。 各点で f\wedge g = \min \{ f, g\} とする。
f_n\wedge g_m は非負単関数であることに注意する。 f_n\wedge g_m \le f_n と f_n \wedge g_m \uparrow_{n} g_m と,上で示したことより,
\!\!\int g_m \, d\mu =\lim_{n\to\infty} \int f_n \wedge g_m \,d\mu \le\lim_{n\to\infty} \int f_n\,d\mu
m\to\infty とすることで,
を得る。 (2),(4) 式より結論を得る。
証明終
3. 一般の可測関数におけるルベーグ積分
一般の可測関数におけるルベーグ積分は,関数を正の部分と負の部分に分けることで定義されます。
定義3(一般の可測関数における積分)
可測関数 \color{red} f\colon X\to \mathbb{R} について, f^+ = \max\{f,0\},\, f^- = \max \{ -f, 0\} としたとき, \int f^+\,d\mu <\infty または \int f^-\, d\mu <\infty が成立するならば
\color{red}\int f\, d\mu = \int f^+ \, d\mu - \int f^- \, d\mu
で定義する(積分値が \pm\infty になっても良い) 。特に, \int |f|\, d\mu = \int f^+ \,d\mu +\int f^- \,d\mu <\infty ならば f は可積分 (積分可能; integrable) であるという。
ここで, a\in\mathbb{R} において,\infty-a=\infty,\, a-\infty =-\infty と定義されることに注意してください。 定義の最後の \int |f|\, d\mu = \int f^+ \,d\mu +\int f^- \,d\mu は後の定理Aでわかります。
可積分ならば, 0\le \int f^+ \, d\mu, \int f^- \, d\mu< \infty ですから,
-\infty <\int f\, d\mu <\infty
すなわち積分は有限値になります。
なお,可測関数は f\colon X\to [-\infty, \infty] のように無限大値を許しても構いません。
4. 区間を絞った積分
区間を絞った積分も導入しておきましょう。 f1_A とは f(x)1_A(x) の意味です。
定義4(区間を絞った積分)
可測関数 f\colon X\to\mathbb{R} と A\in\mathcal{F} に対し,
\color{red}\int_Af\,d\mu = \int f 1_A \, d\mu
を,右辺が意味を持つ限りにおいて定義する。
可測関数 f\colon \mathbb{R}\to \mathbb{R} において, A=[a,b] のときは,\int_Af\, d\mu の代わりに \int_a^bf\,d\mu ともかく。
可測関数 f\colon \mathbb{R}\to \mathbb{R} について, \mu がルベーグ測度のときは, \int f\, d\mu の代わりに,リーマン積分と区別せずに
\color{red} \int f(x)\, dx
とかくことが多いです。リーマン積分と区別しなくて良いのは,リーマン積分可能かつルベーグ積分可能であれば,両者の値が一致することが知られているからです。
ルベーグ積分の例
以下の例は最も基本的で抑えておくべきものです。
例1(ディリクレ関数).
ディリクレ関数 1_\mathbb{Q} (x) = \begin{cases} 1 & x\in\mathbb{Q},\\ 0 & x\in\mathbb{R}\setminus\mathbb{Q} \end{cases} は \mathbb{R} \to \mathbb{R} として非負単関数であり,
\color{red} \int 1_\mathbb{Q}\, dx = \int_\mathbb{Q} dx =0
である。
これは,単関数における積分の定義から \mathrm{Leb} をルベーグ測度としたとき, \int 1_\mathbb{Q}\, dx =\mathrm{Leb}(\mathbb{Q})=0 なので簡単にわかりますね。ディリクレ関数は,リーマン積分不可能だが(ルベーグ測度に関して)ルベーグ積分可能な関数として有名です(→ディリクレ関数の定義と性質5つ)。
上のように,ルベーグ積分はリーマン積分と異なった定義の仕方をすることによって,リーマン積分では積分できなかった関数を積分できるようになるわけですね。
例2(デルタ測度).
(X, \mathcal{F},\delta_x) を測度空間とする。ただし, \delta_x(A) = \begin{cases} 1 & x\in A, \\ 0 & x\not\in A\end{cases} をデルタ測度とする。このとき,可測関数 f\colon X\to\mathbb{R} に対して,
\color{red}\int f \, d\delta_x= f(x)
である。
積分で関数の1点の値を取り出すということも,ルベーグ積分なら可能なわけですね。これも定義から確認可能でしょう。
ルベーグ積分は無限和も表現できます。
例3(無限和の表現).
\mathbb{N}=\{1,2,3,\dots\} とし, (\mathbb{N}, 2^\mathbb{N}, \#) を測度空間とする。ただし, 2^\mathbb{N} はべき集合で,\# はその上の数え上げ測度 (counting measure) とする。このとき, f\colon \mathbb{N}\to[0,\infty) に対して,
\int f\, d\# = \sum_{n=1}^\infty f(n)
である。
ルベーグ積分の諸性質
ここでも, (X,\mathcal{F},\mu) を測度空間とします。
定理A(ルベーグ積分の性質)
可測関数 f\colon X\to \mathbb{R} に対し,以下の各式の積分が定義できる場合に限り,以下の等式が成立する。
- \alpha, \beta \in\mathbb{R} に対し,
\int (\alpha f+\beta g) \,d\mu = \alpha\int f\,d\mu+\beta\int g\,d\mu. - f = g,\, \mu\text{-a.e.} (ほとんどいたるところ)ならば,
\int f\, d\mu = \int g\, d\mu. - f\le g,\, \mu\text{-a.e.} (ほとんどいたるところ)ならば
\int f \,d\mu\le \int g\, d\mu. - \left| \int f\,d\mu \right| \le \int |f|\, d\mu.
- f\ge 0 かつ \int f\, d\mu =0 ならば f=0,\, \mu\text{-a.e.} (ほとんどいたるところ)である。
1.より, A,B\in\mathcal{F} が A\cap B=\emptyset をみたせば,
\int_{A\cup B} f\, d\mu = \int_Af\,d\mu+\int_B f\,d\mu
が積分が意味を持つ範囲において成立することが分かります。
2,5.より, f\ge 0 なら
\color{red}f=0,\, \mu\text{-a.e.}\iff \int f\,d\mu=0
が成立します。
証明
1. \int (\alpha f+\beta g) \,d\mu = \alpha\int f\,d\mu+\beta\int g\,d\mu について
f, g が非負単関数のとき,積分は単に a_k \mu(A_k) の形の有限和であるから,定理1も踏まえて,上の式が成立する。
f,g が非負可測関数のとき,上の事実と定理2から,下から両辺単関数近似することで示したい式が成立する。
f,g が一般の可測関数のとき, f^+, f^{-}, g^{+}, g^{-} に分けることで,積分が意味を持つ範囲において示したい式が成立することがわかる。
2. f=g,\, \mu\text{-a.e} ならば \int f\, d\mu = \int g\, d\mu について
A\in\mathcal{F},\, \mu(A)=0 とする。 B\subset A,\,B\in\mathcal{F} をみたせば, \mu(B)=0 であるから, f が非負単関数のときに \int_A f\, d\mu=0 がわかり,これを踏まえると一般の可測関数で \int_A f\, d\mu=0 がわかる。
仮定より, \mu(f\ne g) = 0 であるから, \int_{\{f\ne g\}} f\,d\mu =\int_{\{ f\ne g\}} g\, d\mu=0 であり,
\begin{aligned}\int f\, d\mu &= \int_{\{f=g\}} f\,d\mu +\int_{\{f\ne g\}} f\, d\mu \\ &= \int_{\{f=g\}} g\, d\mu + 0 \\ &= \int_{\{f= g\}} g\, d\mu + \int_{\{f\ne g\}} g\, d\mu \\ &=\int g\, d\mu. \end{aligned}
3. f\le g, \, \mu\text{-a.e.} ならば \int f \,d\mu\le \int g\, d\mu について
全ての点において,g-f\ge 0 のとき, \int (g-f)\, d\mu \ge 0 はすぐわかる。1.より,移項して \int f\,d\mu\le \int g\,d\mu となる。
2.と同様の議論により,これは f\le g, \, \mu\text{-a.e.} に拡張可能である。
4. \left| \int f\,d\mu \right| \le \int |f|\, d\mu について
\pm f\le |f| と1,3.により,
\pm\int f\, d\mu = \int \pm f \,d\mu \le \int |f|\, d\mu
が成り立つ。すなわち \left| \int f\, d\mu \right| \le \int |f|\, d\mu である。
5. f\ge 0,\, \int f\,d\mu=0\implies f=0,\,\mu\text{-a.e.} について
\begin{aligned}\mu\left(f>\frac{1}{n}\right)&=\int 1_{\{f>1/n\}}\,d\mu \\ &\le n \int f 1_{\{f>1/n\}} \,d\mu \\ & \le n\int f \, d\mu = 0 \end{aligned}
であるから, \mu(f>1/n) = 0 である。 n\uparrow \infty とすると, \{ f>1/n\} \uparrow \{ f>0\} であるから, \mu(f>0)=0 となる。 f\ge 0 より, f=0,\, \mu\text{-a.e.} である。
証明終
複素数値の積分
可測関数 f\colon X\to \mathbb{C} に対する積分を考えましょう。 f が可測であることと, \operatorname{Re} f, \operatorname{Im} f \colon X\to \mathbb{R} が可測であることは同値であることが知られています。
f の積分は, \operatorname{Re} f, \operatorname{Im} f の積分が定義できる場合に限り定義して,
\color{red}\int f\, d\mu = \int \operatorname{Re} f\, d\mu+i \int \operatorname{Im} f\, d\mu
で定義します。このとき,上で述べた定理Aが,複素積分の場合にも成り立ちます。
収束定理
ルベーグ積分の最大のメリットは,極限の議論がリーマン積分のときよりも簡単なことでしょう。特に,以下の3つの定理は大切です。続けて確認するとよいかもしれません。