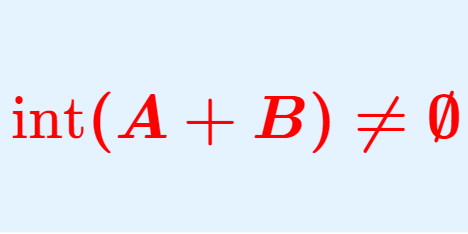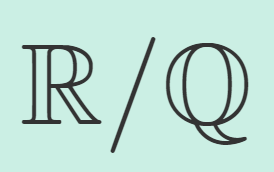測度論におけるシュタインハウスの定理とその証明

$\R^N$ における可測集合は，それ自身はなかなか実態がよくわからないものかもしれません。しかし，零集合でない可測集合を2つ用意して， $A+B=\{a+b\mid a\in A,\, b\in B\}$ を考えると，これは開集合を含むようになります。

シュタインハウスの定理といわれる本定理を紹介し，証明しましょう。

測度論におけるシュタインハウスの定理
シュタインハウスの定理の準備
シュタインハウスの定理の証明
参考

測度論におけるシュタインハウスの定理

シュタインハウスの定理 (Steinhaus theorem)

$\mu$ を $\R^N$ 上のルベーグ測度とし，可測集合 $A,B\subset \R^N$ は $\mu(A),\mu(B)>0$ をみたすとする。

A+B=\{a+b\mid a\in A,\, b\in B\}

と定めると， $\color{red}\boldsymbol{\operatorname{int}(A+B)\ne \emptyset}$ である。ただし， $\operatorname{int}$ は集合の内部(開核; interior)を指す。

特に， $N=1$ とすると，次の主張になります。

シュタインハウスの定理 1次元版

$\mu$ を $\R$ 上のルベーグ測度とし，可測集合 $A,B\subset \R$ は $\mu(A),\mu(B)>0$ をみたすとする。

A+B=\{a+b\mid a\in A,\, b\in B\}

と定めると， $A+B$ は区間を含む。すなわち， $[s,t] \subset A+B$ となる $s,t\in\R$ が存在する。

ルベーグ測度が正になるような集合が2つあれば， $A+B$ と組み合わせることで，集合の内部が空集合にならないようにできる，と言っています。なお，基本的な話ですが， $\mu(A)>0$ であっても， $\operatorname{int}(A)=\emptyset$ となることはあり得ることに注意しましょう。今回の定理は，あくまで集合 $A,B$ を $A+B$ のように組み合わせていることが大切です。

たとえば， $A=\R\setminus \mathbb{Q}$ とすると， $\mu(A)=\infty>0$ ですが， $\operatorname{int}(A)=\emptyset$ ですね。

一方， $A+A = \R\setminus \mathbb{Q}+\R\setminus \mathbb{Q} = \R$ となり，区間を含みます。
実際， $r\in R$ が無理数なら， $r/2+r/2\in \R\setminus \mathbb{Q}+\R\setminus \mathbb{Q}$ ですし， $q\in\mathbb{Q}$ なら， $q=(q/2+\sqrt{2})+(q/2-\sqrt{2})\in \R\setminus \mathbb{Q}+\R\setminus \mathbb{Q}$ ですね。

シュタインハウスの定理の準備

シュタインハウスの定理そのものの証明の前に，一つ証明の準備をしましょう。

補題（対称差と測度）

$(X,\mathcal{F},\mu)$ を測度空間とし， $A,B,C\in\mathcal{F}$ ， $\mu(A)<\infty$ とする。このとき，

\color{red}|\mu(A\cap B)-\mu(A\cap C)|\le \mu(B\triangle C)

が成り立つ。ただし， $B\triangle C = (B\setminus C)\cup (C\setminus B)$ は集合 $B,C$ の対称差を表す。

証明しましょう。

証明

\begin{aligned}&\mu(A\cap B)-\mu(A\cap C)\\ &=\{\mu(A\cap B\cap C)+\mu(A\cap B\cap C^c)\} \\ &\quad -\{ \mu(A\cap B\cap C)+\mu(A\cap B^c\cap C) \} \\ &=\mu(A\cap B\cap C^c) -\mu(A\cap B^c \cap C). \end{aligned}

同様に，

\begin{aligned} &\mu(A\cap C)-\mu(A\cap B) \\ &=\mu(A\cap B^c\cap C) -\mu(A\cap B \cap C^c) \end{aligned}

であるから，

\begin{aligned} &|\mu(A\cap B)-\mu(A\cap C)| \\ &\le \mu(A\cap B\cap C^c) +\mu(A\cap B^c \cap C) \\ &\le \mu(B\cap C^c)+\mu(B^c\cap C) \\ &= \mu(B\triangle C) \end{aligned}

となって，結論を得る。

証明終

シュタインハウスの定理の証明

この定理の証明は様々なやり方が知られているようですが，ここでは，[1] の Theorem 3.7.1 で示します。

証明

ルベーグ測度の内部正則性より， $A_0\subset A,\, B_0\subset B$ をコンパクト集合として， $\mu(A_0)>0,\, \mu(B_0)>0$ とできる（このとき， $\operatorname{int} (A_0) \ne \emptyset, \operatorname{int}(B_0)\ne\emptyset$ のいずれかが成り立つなら証明は一瞬である）。

よって特に， $A,B$ はコンパクト集合とし， $\mu(A)>0,\,\mu(B)>0$ と思ってよい。

$t\in \R^N$ に対し， $B_t=t-B=\{t-b\mid b\in B\}$ とおく。関数 $\omega\colon \R^N\to \R$ を

\omega(t)=\mu(A\cap B_t) = \int_{\R^N} 1_A(x)1_{B_t}(x)\, dx

と定める。ただし， $1$ は定義関数(特性関数，指示関数)を表す。 $\omega$ が連続関数であることを示そう。

$\varepsilon >0$ とする。ルベーグ測度の外部正則性より， $B_t\subset G_t$ となる開集合 $G_t$ で， $\mu(G_t\setminus B_t)<\varepsilon$ となるものが存在する。 $B_t\subset G_t$ より， $B_t\cap G_t^c=\emptyset$ であり， $B_t, G_t^c$ はどちらも閉集合であるから，その距離 $\delta>0$ が取れる。

$\| h\|<\delta$ となる $h\in \R^N$ をとる。ただし， $\|h\|$ はユークリッド距離(ノルム)を指す。このとき， $B_{t+h}\subset G_t$ であり，

\begin{equation} \mu(B_{t+h}\setminus B_t)\le \mu(G_t\setminus B_t)< \varepsilon \end{equation}

となる。一方で， $B_{t+h} = B_t+h$ であるから，ルベーグ測度の平行移動不変性より， $\mu(B_{t+h})=\mu(B_t)$ である。ゆえに，

\begin{align}\mu(B_t\setminus B_{t+h}) &\le\mu( G_t\setminus B_{t+h} ) \\ &= \mu(G_t)-\mu(B_{t+h}) \\ &= \mu(G_t)-\mu(B_t) \\ &= \mu(G_t\setminus B_t) <\varepsilon. \end{align}

$\text{(1)--(5)}$ 式より， $\|h\|<\delta$ に対し，

\begin{aligned}\mu(B_{t+h}\triangle B_t)& = \mu(B_{t+h}\setminus B_t)+\mu(B_t\setminus B_{t+h} ) \\&<\varepsilon \end{aligned}

となる。これと，上の補題(準備)より，

\begin{aligned}&|\omega(t+h)-\omega(t)|\\&= |\mu(A\cap B_{t+h})-\mu(A\cap B_t)| \\ &\le \mu(B_{t+h}\triangle B_t) <\varepsilon \end{aligned}

となるから， $\omega$ が連続であることが示せた。次に， $\omega (t)>0$ となる $t\in \R^N$ の存在を示そう。 $\omega$ の定義より， $\omega\ge 0$ である。

\begin{aligned}&\int_{\R^N} \omega(t)\, dt \\&= \int_{\R^N} \int_{\R^N} 1_A(x)1_{B_t}(x)\, dxdt\\ &= \int_{\R^N } 1_A(x)\left(\int_{\R^N } 1_{B_t}(x)\, dt\right)dx\\ &= \int_{\R^N } 1_A(x)\left(\int_{\R^N } 1_{B}(t-x)\, dt\right)\!\!dx\\ &= \int_{\R^N } 1_A(x)\left(\int_{\R^N } 1_{B}(u)\, du\right)dx\\ &= \int_{\R^N } 1_A(x)\, dx \int_{\R^N } 1_{B}(u)\, du\\ &= \mu(A)\mu(B)>0 \end{aligned}

であるから， $\omega(t) >0$ となる $t\in \R^N$ の存在が分かった。

最後に定理の結論を示そう。 $\omega(t_0)>0$ となる $t_0\in \R^N$ をとる。 $\omega$ は連続関数より，開近傍 $t_0\in U$ で， $U$ 上 $\omega>0$ となるものが存在する。すなわち， $t\in U$ なら $\mu(A\cap B_t)>0$ である。

特に， $A\cap B_t\ne \emptyset$ であり，任意の $t\in U$ に対して，ある $a\in A\cap B_t = A\cap (t-B)$ となるものが存在する。 $a\in t-B$ より，ある $b\in B$ を用いて， $a=t-b$ とかける。

$t=a+b \in A+B$ が $t\in U$ で成立するので， $U\subset A+B$ である。したがって， $\operatorname{int}(A+B)\ne \emptyset$ となる。

証明終

少し長いと感じたかもしれませんが，無事に証明できましたね。