概一様収束とは,任意に小さなある正の測度の集合を除けば一様収束するという意味です。有限測度空間で各点収束すれば,概一様収束するというのがエゴロフの定理です。
概一様収束とエゴロフの定理について,その定義と証明を解説しましょう。
概一様収束とは
まずは概一様収束の定義と基本的な性質を紹介しましょう。
概一様収束の定義
定義(概一様収束)
(X,\mathcal{F},\mu) を測度空間, \{f_n\colon X\to\mathbb{R}\} を可測関数の列, f\colon X\to\mathbb{R} を可測関数とする。
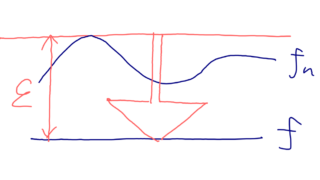
任意の \varepsilon>0 に対して,ある A\in\mathcal{F} が存在して, \mu(A^c)<\varepsilon かつ \{f_n\} が f に A 上一様収束する,すなわち \mu(A^c)<\varepsilon かつ
\lim_{n\to\infty}\sup_{x\in A}|f_n(x)-f(x)|=0
となるとき, \{f_n\} は f に概一様収束 (almost uniform convergence) するという。
小さな正の測度の部分を除けば,一様収束していることを概一様収束というんですね。
概一様収束すれば零集合以外で各点収束する
f_n\xrightarrow{n\to\infty} f が概一様収束すれば, f_n \to f,\,\mu\text{-a.e.} (すなわち零集合以外で各点収束する)が成立します。
実際, \mu(B)>0 となる B\in\mathcal{F} 上各点収束しないとすると,概一様収束の定義が \varepsilon =\mu(B)/2 としても成立することに矛盾しますね。
なお,有限測度空間ならこの逆も成立するというのがエゴロフの定理です。後で紹介しましょう。
概一様収束しても零集合以外で一様収束するとは限らない
概一様収束の定義はあくまで \mu(A^c)<\varepsilon となる A 上一様収束であり, \mu(A^c)=0 となる A 上一様収束(零集合以外で一様収束)というわけではありません。
これはよく勘違いされるところなので,注意が必要です。たとえば,
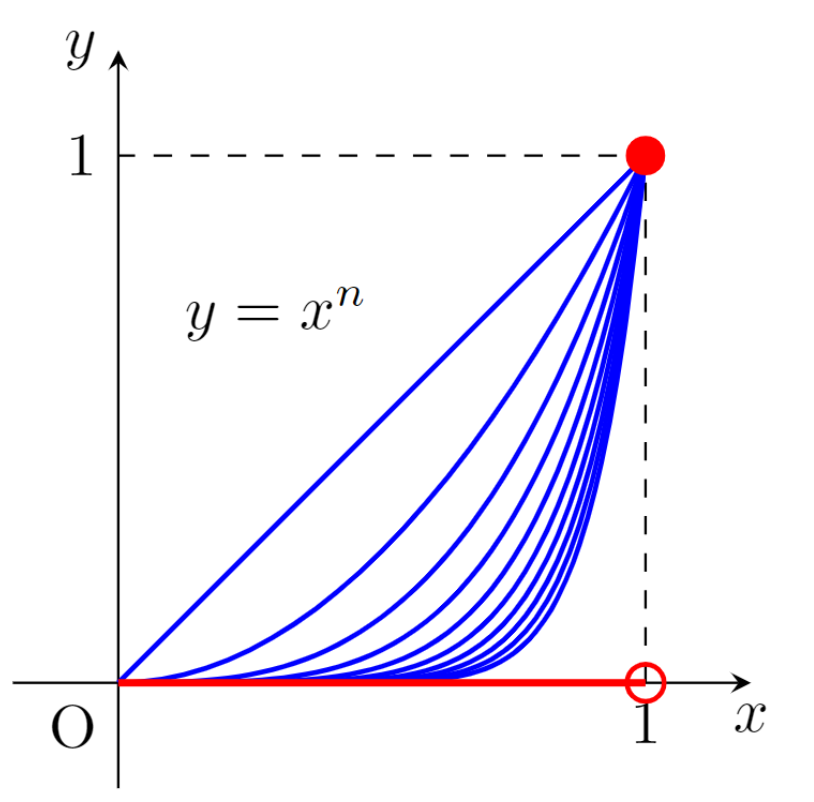
f_n(x)=x^n\quad(0\le x\le 1)
を考えましょう。この関数は [0,1] 上 f(x)=\begin{cases} 1 & x=1, \\ 0 & 0\le x<1\end{cases} に概一様収束しますが,零集合以外で一様収束しません。
実際,任意の十分小さい \varepsilon >0 に対し, \{f_n\} は [0,1-\varepsilon] 上一様収束するため,概一様収束します。
一方で,任意の零集合 N\subset [0,1] に対し, [0,1)\setminus N は 1 にどれだけでも近い値が取れるので, [0,1]\setminus N 上一様収束しません。
エゴロフの定理
有限測度空間なら,零集合以外で各点収束すれば概一様収束するというのが,エゴロフの定理 (Egorov’s theorem, Egoroff’s theorem) です。
エゴロフの定理 (Egorov’s theorem)
(X,\mathcal{F},\mu) を \color{red} \mu(X)<\infty をみたす測度空間, \{f_n\colon X\to\mathbb{R}\} を可測関数の列, f\colon X\to\mathbb{R} を可測関数とする。
このとき,f_n \xrightarrow{n\to\infty} f,\; \mu\text{-a.e.} ならば, \{f_n\} は f に概一様収束する。
すなわち任意の \varepsilon>0 に対しある A\in\mathcal{F} が存在して, \mu(A^c)<\varepsilon かつ A 上一様収束する。
なお, \mu(X)<\infty でないと反例があります。たとえば, f_n=1_{[n,n+1]} とおくと,各点で f_n\to 0 ですが,測度が小さな集合(具体的にはたとえば \mu(A^c)<1/2 とか)を除いても \sup_{x\in A}|f_n-0| =1 ですから,概一様収束しません。
証明しましょう。
証明
零集合上の値を修正しても測度に影響を与えないので,各点で f_n\to f と仮定してよい。 \varepsilon>0 と整数 m\ge 1 を任意に取る。
A_{m,n}=\bigcap_{k\ge n}\{ |f_k-f|<1/2^m\}
とおくと,仮定より A_{m,n} \uparrow_n X が成り立つ( n について単調増加で X=\bigcup_{n\ge 1} A_{m,n} の意味)。よって \mu(A_{m,n})\uparrow_n \mu(X) である。
\mu(X)<\infty より,ある N_m\ge 1 が存在して,
n\ge N_m\implies \mu(A_{m,n})>\mu(X)-\varepsilon/2^m
特に \mu(A_{m,N_m}^c)<\varepsilon/2^m とできる。 A=\bigcap_{m\ge 1} A_{m,N_m} と定めると,
であり,
であるから,任意の m\ge 1,\, k\ge N_m ,\,x\in A に対して,|f_k(x) -f(x)|<1/2^m とできる。よって概一様収束する。
証明終