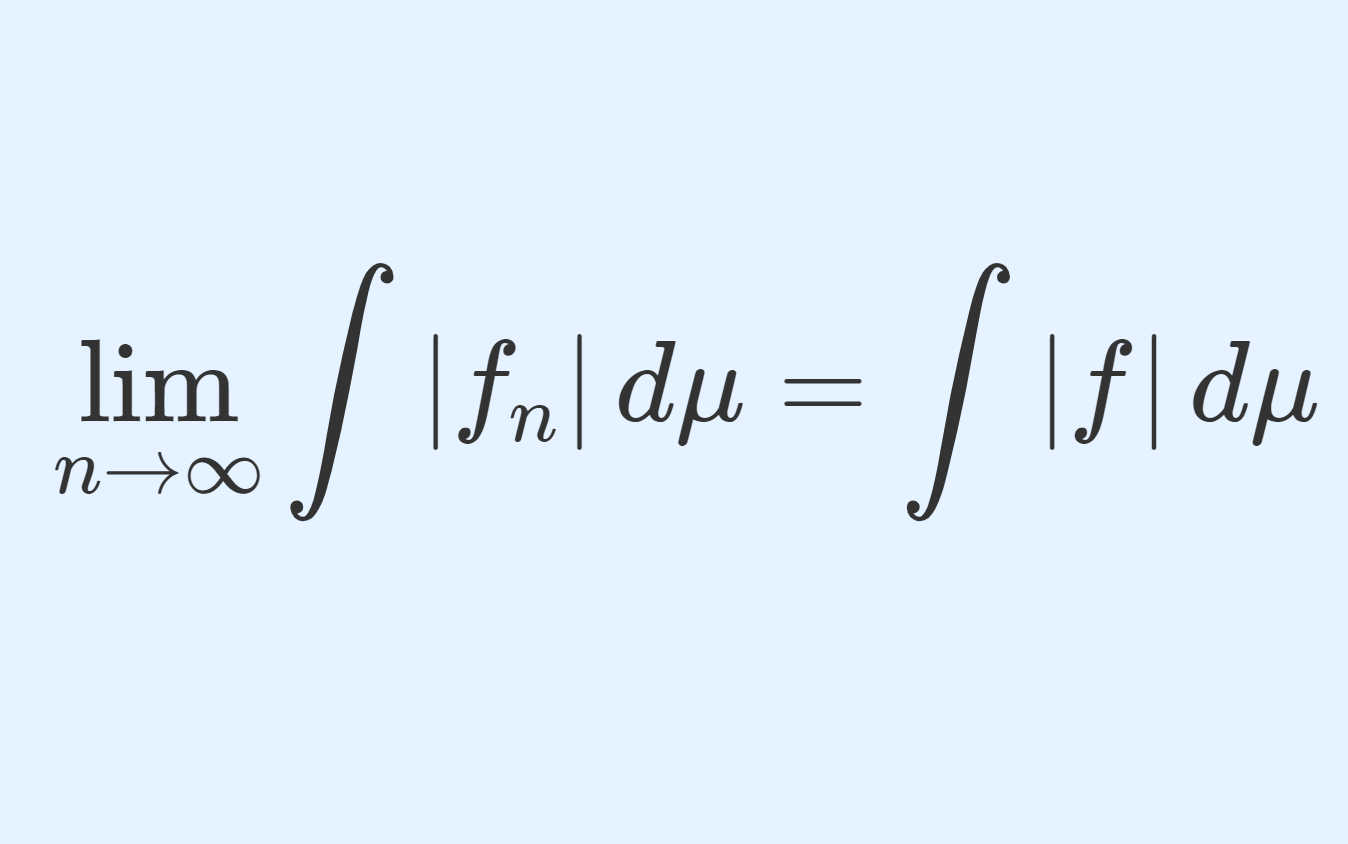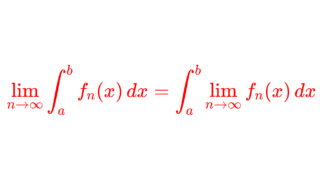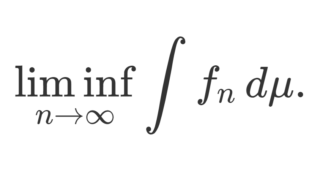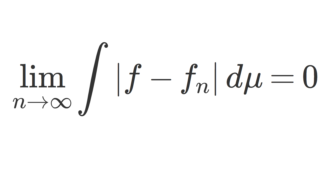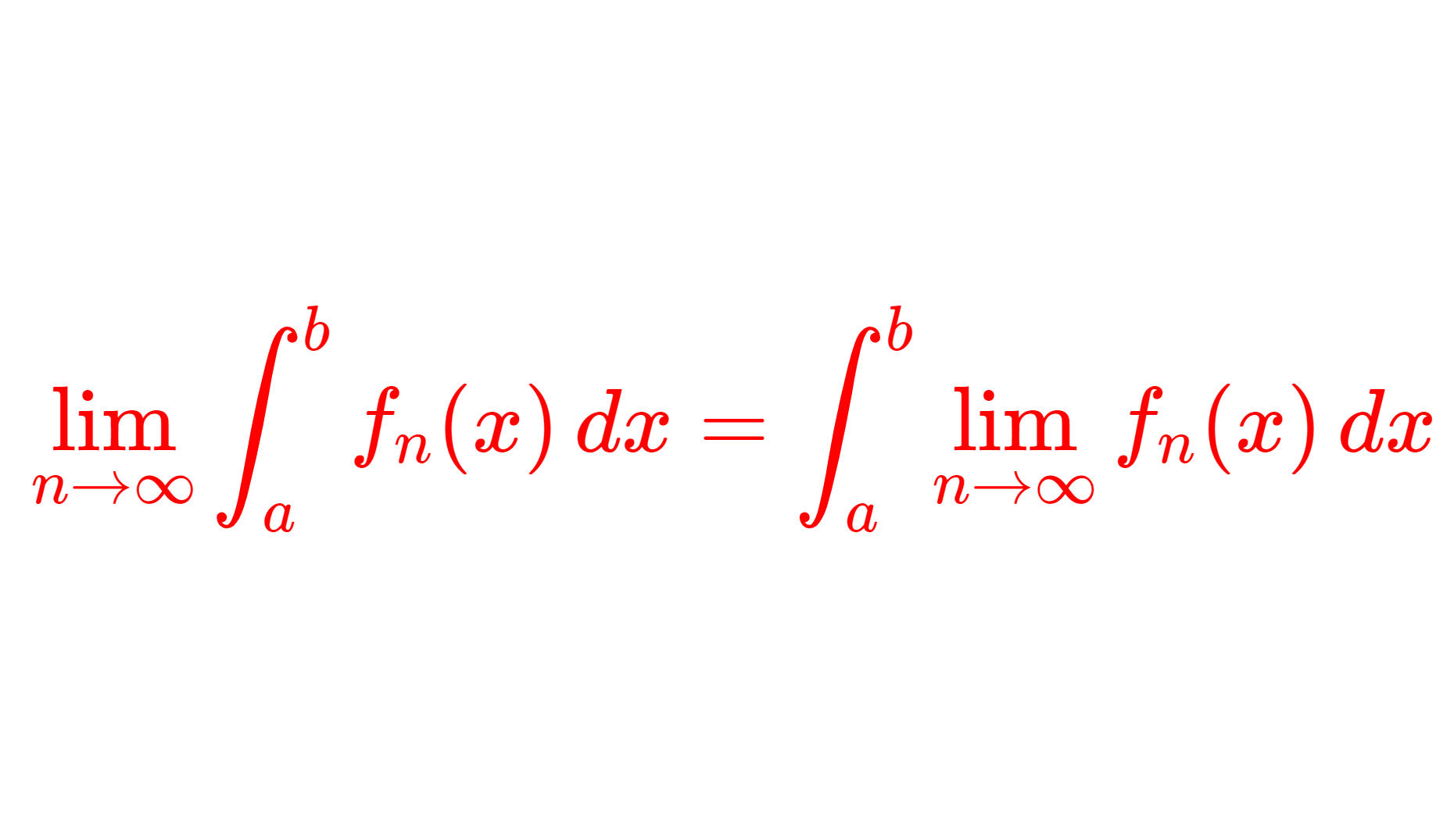Schefféの補題 (Scheffé’s lemma) とは,収束定理(極限と積分の交換定理)の1つで,絶対値をつけた積分の値が消滅しなければ,極限と積分を交換することが可能であるという定理です。Schefféの補題について,その主張と証明を行いましょう。
Schefféの補題
定理(Schefféの補題)
(X,\mathcal{F},\mu) を測度空間, \{f_n\} をその上の可測関数列としさらに, f_n \xrightarrow{n\to\infty} f, \, \mu\text{-a.e.} (ほとんどいたるところ各点収束)かつ
\begin{equation}\lim_{n\to\infty}\int |f_n|\,d\mu = \int |f|\,d\mu<\infty \end{equation}
が成立するとする。このとき,
が成り立つ。特に,
も成り立つ。
最後の式 (3) を言い換えると,
\lim_{n\to\infty} \int f_n\,d\mu = \int \lim_{n\to\infty} f_n\,d\mu
ですから,極限と積分の交換定理ですね。
Fatouの補題より, f_n \xrightarrow{n\to\infty} f,\,\mu\text{-a.e.} ならば常に
\int |f|\,d\mu \le \liminf_{n\to\infty}\int |f_n|\,d\mu
が成り立つのでした(→Fatouの補題とその証明・具体例・活用例)。今回は仮定に積分が消滅しない条件 (1) 式を課すことで,定理を成立させているわけです。
積分が消滅しない仮定 (1) 式がないと,本定理は成立しません。たとえば, f_n=1_{[n,n+1]} とすれば,仮定 (1) 式は満たさず,定理の結論も成り立ちませんね。
結論の式 (2) が成立すれば, (1) 式も成立します。実際,
\begin{aligned}\left|\int |f_n|\,d\mu - \int| f|\,d\mu\right|&\le \int |f_n-f|\,d\mu \\ &\xrightarrow{n\to\infty} 0 \end{aligned}
ですね。このように, f_n \to f の下では, (1)\iff (2) となります。極限と積分の交換には,積分が消滅しない( (1) 式)ことが肝なわけです。
Schefféの補題の証明
証明はFatouの補題を使うだけです。
証明
g_n =|f|+|f_n|-|f-f_n| とすると, g_n \ge 0 かつ g_n \to 2|f| である。 g_n にFatouの補題を適用して,
\begin{aligned}&2\int |f|\,d\mu \\&= \int\lim_{n\to\infty} g_n\,d\mu \\ &\le \liminf_{n\to\infty}\int g_n\,d\mu \\ &= 2\int |f|\,d\mu -\limsup_{n\to\infty} \int|f-f_n|\,d\mu \end{aligned}
より, \lim_{n\to\infty } \int|f-f_n|\,d\mu = 0 を得る。後半は
から得る。
証明終
L^p空間への一般化
以下で, f\in L^p(\Omega) とは,\lVert f\rVert_p=\left( \int_{\Omega} |f|^p\,d\mu\right)^{1/p}<\infty ( p 乗可積分)を指します。
定理 (F. Riesz)
(\Omega,\mathcal{F},\mu) を測度空間, 1\le p< \infty とする。
\{f_n\}\subset L^p(\Omega) が f_n \xrightarrow{n\to\infty} f \in L^p(\Omega),\, \mu\text{-a.e.} かつ \lim_{n\to\infty}\lVert f_n \rVert_p = \lVert f\rVert_p をみたすとすると,
\color{red} \lim_{n\to\infty} \lVert f_n -f\rVert_p =0
が成り立つ。
一般化といいましたが,こちらの定理の方が歴史的に早いようです。
証明は g_n = 2^{p-1}(|f|^p+|f_n|^p)-|f-f_n|^p とすれば上と同じです( y=|x|^p は凸関数なので g_n\ge 0 に注意)。