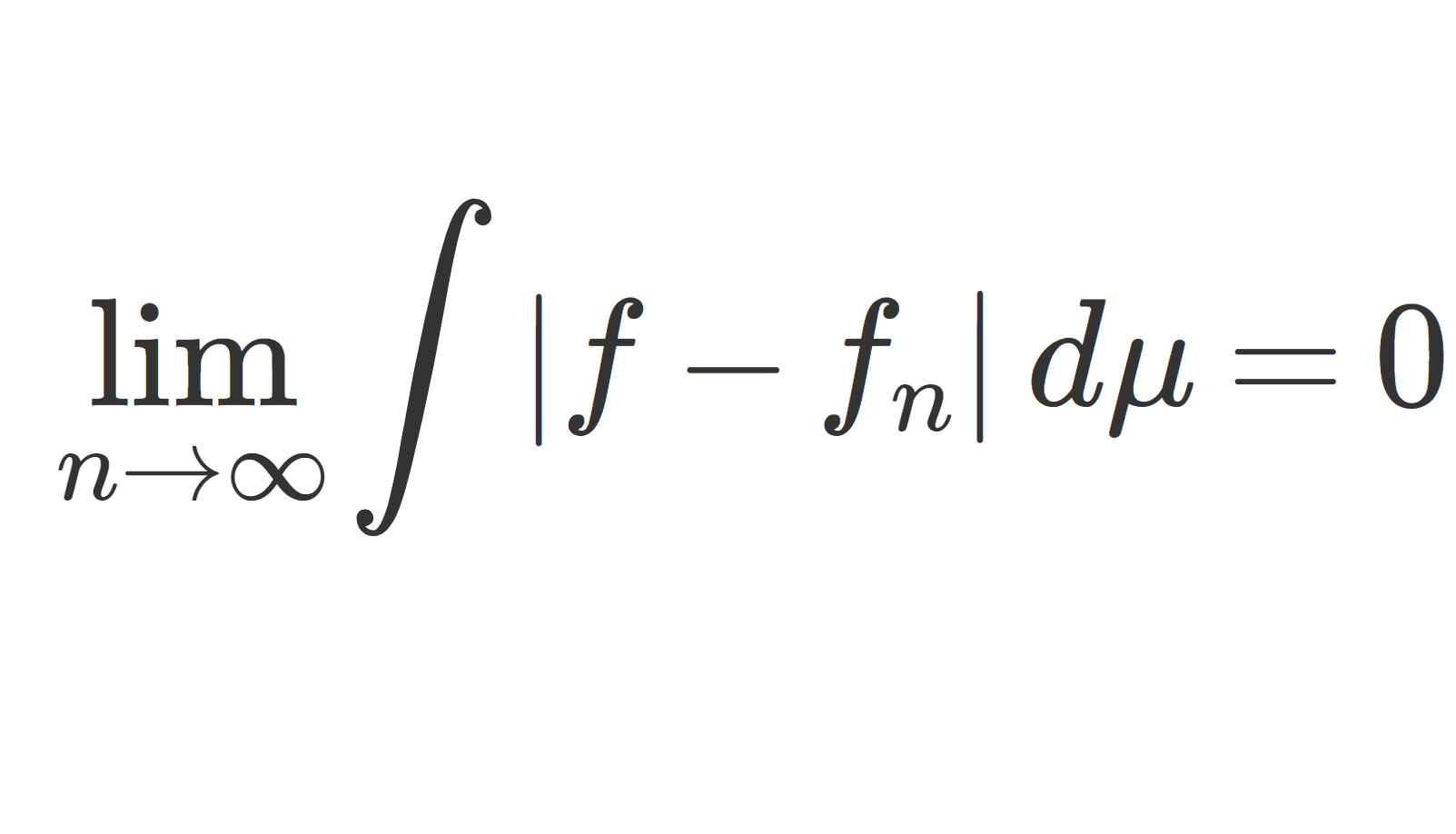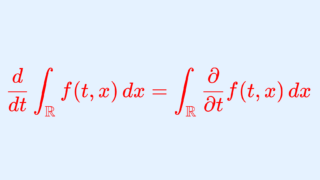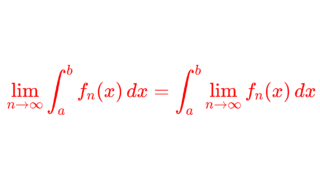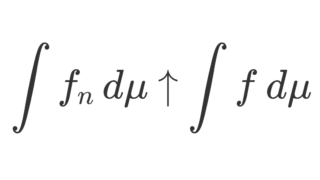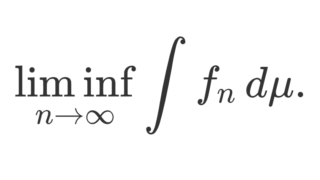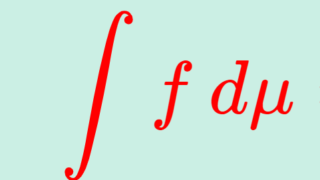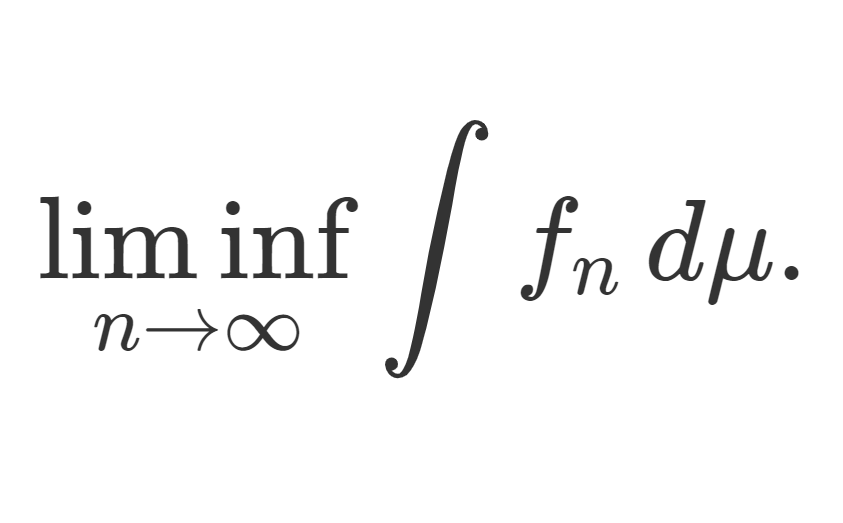ルベーグの収束定理(優収束定理)とその例題・証明

ルベーグの収束定理 (優収束定理; dominated convergence theorem, DCT) とは，ルベーグ積分・測度論における「積分と極限の交換定理」の1つで，ルベーグ積分の根幹をなす定理といえます。

ルベーグの収束定理について，その主張と例題・証明を行っていきましょう。

ルベーグの収束定理(優収束定理)
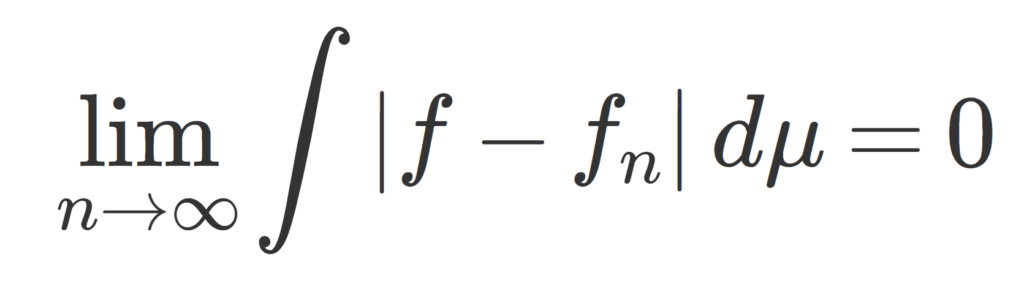
1. ルベーグの収束定理(優収束定理)
2. 有界収束定理
ルベーグの収束定理(優収束定理)の例題
ルベーグの収束定理(優収束定理)の証明
微分と積分の交換定理
関連する記事

ルベーグの収束定理(優収束定理)

定理1（ルベーグの収束定理）

$(X,\mathcal{F},\mu)$ を測度空間， $\{f_n\}$ をその上の可測関数列とし，以下の2つの条件

$f_n \xrightarrow{n\to\infty} f$
$|f_n|\le F \; (n\ge 1)$ となる可積分関数 $F$ が存在する

の両方が成立するとき， $f_n, f$ は可積分で

\color{red}\lim_{n\to\infty} \int |f_n-f|\,d\mu = 0

が成り立つ。特に，

\color{red}\lim_{n\to\infty} \int f_n\,d\mu =\int f\,d\mu

である。(このときの $F$ を優関数 (dominating function) と呼ぶ)

ここで $f$ が可積分 (integrable) とは， $\int |f|\,d\mu<\infty$ が成り立つことでした。

後半の等式を書き換えると，

\color{red}\lim_{n\to\infty} \int f_n\,d\mu =\int \lim_{n\to\infty}f_n\,d\mu

ですから，積分と極限の交換定理ですね。ルベーグ積分はリーマン積分に比べて，積分と極限の交換が行いやすいというメリットがあり，その根幹をなすのがこの定理です。単調収束定理・Fatouの補題と並び，ルベーグ積分における最も大事な定理と言っても良いでしょう。

なお， $f_n \xrightarrow{n\to\infty} f$ や $|f_n|\le F \; (n\ge 1)$ の部分は，各点ではなく $\mu\text{-a.e.}$ でも構いません。零集合( $\mu(N)=0$ となる集合 $N$ )上の関数の値は積分に影響しないからです。

なお，可積分優関数 $F$ の存在を仮定しないと反例があります。実際， $f_n=1_{[n,n+1]}$ とすると，

\begin{gathered}\lim_{n\to\infty} \int 1_{[n,n+1]}\,d\mu =1,\\ \int \lim_{n\to\infty} 1_{[n,n+1]}\, d\mu = \int 0\,d\mu = 0 \end{gathered}

となって，値が一致していませんね。

有界収束定理

特に，有限測度空間 $\mu(X)<\infty$ のときは，有界収束定理と呼ばれる以下の定理が成立します。「ルベーグの収束定理」の特別なバージョンです。

定理2（有界収束定理）

$(X,\mathcal{F},\mu)$ を $\color{red} \mu(X)<\infty$ をみたす測度空間， $\{f_n\}$ をその上の可測関数列とし，以下の2つの条件

$f_n \xrightarrow{n\to\infty} f$
$|f_n|\le M\; (n\ge 1)$ となる定数 $M$ が存在する( $n$ によらず一様に有界)

の両方が成立するとき， $f_n, f$ は可積分で

\color{red}\lim_{n\to\infty} \int |f_n-f|\,d\mu = 0

が成り立つ。特に，

\color{red}\lim_{n\to\infty} \int f_n\,d\mu =\int f\,d\mu

である。

これの証明はルベーグの収束定理を認めれば簡単です。 $\mu(X)<\infty$ なら定数関数 $M \ge 0$ は $\int M\,d\mu = M\mu(X)<\infty$ で可積分ですから， $M$ が可積分優関数となるからです。

ルベーグの収束定理(優収束定理)の例題

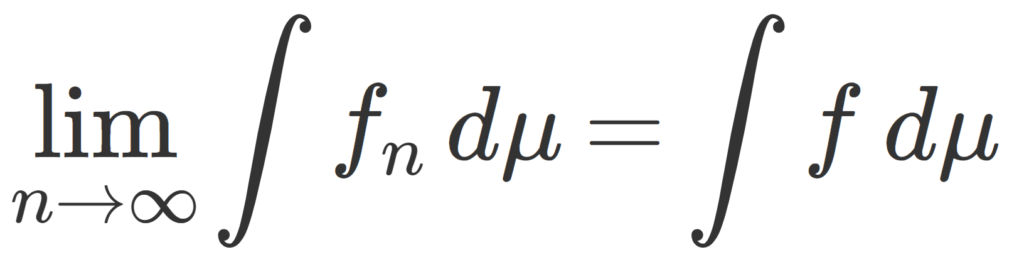
例題1.

$\displaystyle \lim_{n\to\infty} \int_0^\infty \frac{1}{1+x^n}\, dx$ を求めよ。

$n\ge 2$ に対し， $\left|\dfrac{1}{1+x^n}\right| \le \min\left\{1, \dfrac{1}{x^2} \right\}$ であり，右辺は $n$ によらずかつ $(0,\infty)$ 上可積分ですから，ルベーグの収束定理より

\begin{aligned} \lim_{n\to\infty} \int_0^\infty \frac{1}{1+x^n}\, dx &= \int_0^\infty\lim_{n\to\infty} \frac{1}{1+x^n}\, dx \\ &= \int_0^\infty \left(1_{[0,1)}+ \frac{1_{\{1\}}}{2} \right)\, dx \\&= 1 \end{aligned}

となりますね。優関数は $n$ によらずに取らねばならないことに注意してください。たとえば，答案に $\left|\dfrac{1}{1+x^n}\right| \le \min\left\{1, \dfrac{1}{x^n} \right\}$ と書いてしまうと減点されるでしょう。初学者はココを間違いがちです。

例題2.

$\displaystyle\lim_{n\to\infty} \int_0^{\pi/2} \sin^n \theta \,d\theta$ を求めよ。

$|\sin^n\theta|\le 1$ かつ $\sin^n \theta \xrightarrow{n\to\infty} 0,\; \text{a.e.}$ より，有界収束定理から

\lim_{n\to\infty} \int_0^{\pi/2} \sin^n \theta \,d\theta = \int_0^{\pi/2} 0 \,d\theta = 0

ですね。なお， $\int_0^{\pi/2} \sin^n \theta \,d\theta$ 自体を計算したい場合は【ウォリス積分】sin,cosのn乗積分の導出と性質で解説しています。

もう一問やってみましょう。以下で，優関数は $t$ に依存せず取らねばならないことに注意してください。

例題3.

$\displaystyle \lim_{t\to\infty} \int_1^\infty tx e^{-tx^3} \,dx$ を求めよ。

$f(t)= tx e^{-tx^3}$ とおくと， $f'(t)= (x-tx^4) e^{-tx^3}$ から関数の増減を考えることで， $|f(t)|\le 1/x^2$ がわかります。右辺は $(1,\infty)$ 上可積分より，ルベーグの収束定理が使えて， $\lim_{t\to\infty} \int_1^\infty tx e^{-tx^3} \,dx = \int_1^\infty \lim_{t\to\infty}tx e^{-tx^3} \,dx=0$

が求まります。

ここで，ルベーグの収束定理は「列の極限の定理」より，本来は点列 $\{t_n\}$ を $t_n\xrightarrow{n\to\infty} \infty$ となるように取って適用せねばなりません。しかし，どんな点列をとっても積分の極限は $0$ になりますから，結局 $t\to\infty$ で考えてもいい訳です(→実数上関数の収束と数列の収束の同値性とその証明)。