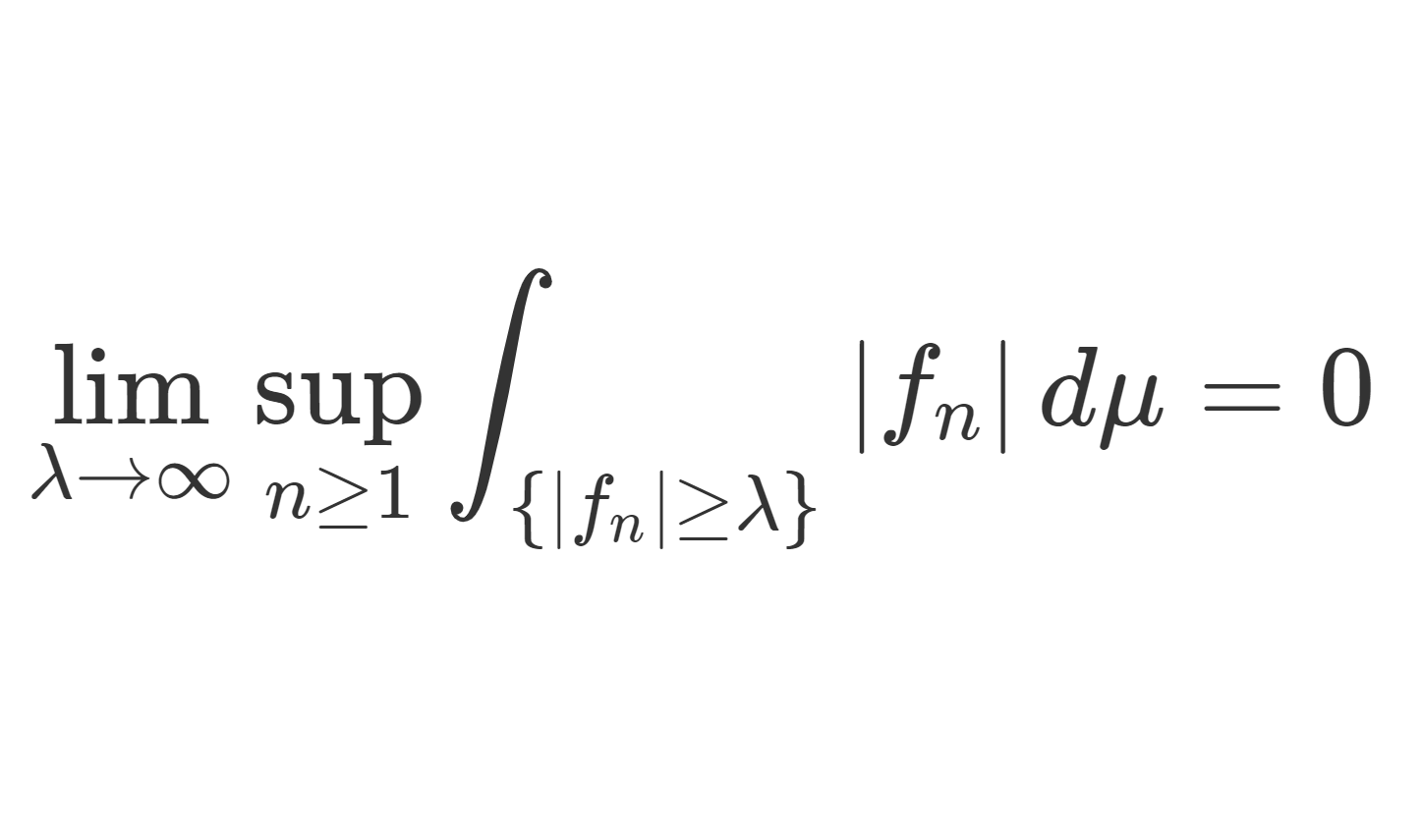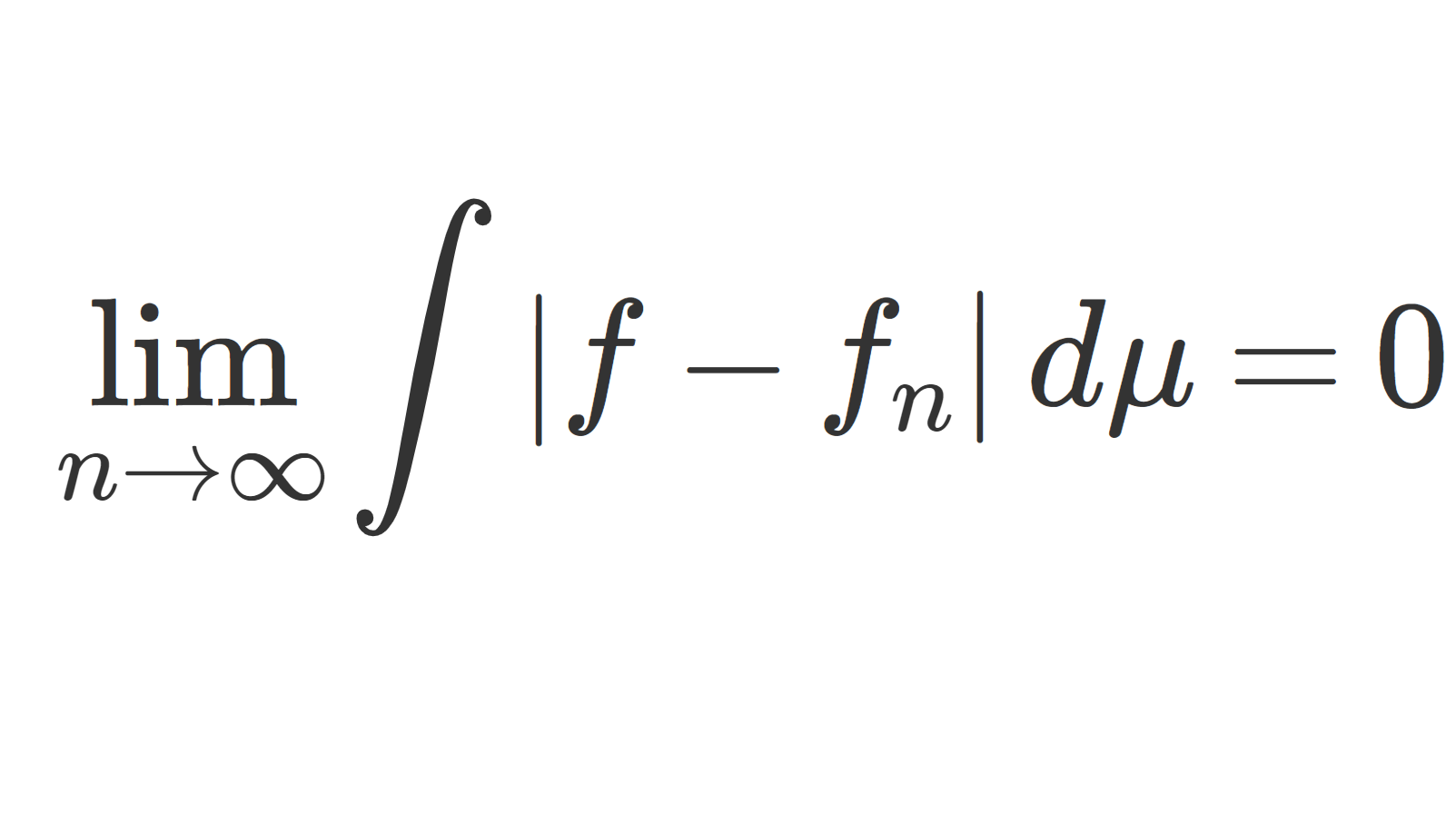一様可積分性は,とくに有限測度( \mu(X)<\infty)のときに有用です。ここでは,一様可積分性の定義と,一様可積分のときに用いることのできる「ヴィタリの収束定理」について解説していきましょう。
一様可積分性
可測関数 f が可積分 (integrable) であるとは, \int |f|\,d\mu<\infty が成立することでした。
一様可積分性の定義
定義(一様可積分)
可積分関数列 \{f_n\} が一様可積分 (uniformly integrable) であるとは,
\color{red}\lim_{\lambda\to\infty} \sup_{n\ge 1} \int_{\{|f_n|\ge \lambda\}} |f_n| \,d\mu=0
が成り立つことを言う。
一様可積分は,特に有限測度( \mu(X)<\infty)のときに大事な概念であり,確率論でもよく使われます。
一様可積分は,任意の \varepsilon>0 に対して,ある \delta>0 が存在して,
\color{red}\begin{equation} \mu(A)<\delta \implies \left|\int_A f_n\,d\mu\right|<\varepsilon\;(n\ge 1) \end{equation}
と定義することもあります。この定義は上の定義より少し緩いです。実際, \mu(X)<\infty のとき,以下の同値が知られています。
一様可積分性の同値な定義
定理1(一様可積分性の同値な定義)
\color{red} \mu(X)<\infty であるとき,可測関数列 \{f_n\} に関して以下は同値。
- \{f_n\} は一様可積分
- 上式 (1) かつ \begin{equation}\sup_{n\ge 1} \int |f_n|\,d\mu<\infty \end{equation} が成立。
(1) 式だけでは,元の定義と同値になりません。実際, f_n =n1_{\{0\}} で, \mu=\delta_0 (デルタ測度) とすると, (1) 式は満たしますが,元の定義は満たしません。
証明
1. \implies 2.について
\lambda>0 が十分大きいとき,1.より \sup_n\int_{\{|f_n|\ge \lambda\}}|f_n|\,d\mu<\infty である(左辺を M_\lambda とする)。
\begin{aligned}&\sup_n \int |f_n|\,d\mu \\ &\le \sup_n \int_{\{|f_n|<\lambda\}} |f_n|\,d\mu+ \sup_n\int_{\{|f_n|\ge\lambda\}} |f_n|\,d\mu \\ &\le \sup_n \int\lambda\,d\mu + M_\lambda\\ &\le \lambda\mu(X)+M_\lambda<\infty \end{aligned}
より, (2) 式を得る。また, \varepsilon>0 に対して, \sup_n \int_{\{f_n\ge \lambda\}} |f_n|\,d\mu<\varepsilon をみたす \lambda を取ると, \mu(A)<\varepsilon/\lambda に対して,
より, (1) 式を得る。
2. \implies 1.について
(2) 式より,M=\sup_n\int |f_n|\,d\mu<\infty とする。 \lambda >0 に対し,
\begin{aligned}\lambda\mu(|f_n|\ge \lambda) &=\lambda \int_{\{|f_n|\ge \lambda\}}\,d\mu \\ &\le \int_{\{|f_n|\ge \lambda\}}|f_n|\,d\mu \le M \end{aligned}
より, \mu(|f_n|\ge \lambda) \le M/\lambda である(マルコフの不等式)。 (1) 式より M/\lambda<\delta とすると,特に \mu( \{|f_n|\ge \lambda \} \cap \{f_n\ge 0\})<\delta, \mu( \{|f_n|\ge \lambda \} \cap \{f_n< 0\})<\delta であるから,
これは, \lim_{\lambda\to\infty} \sup_n \int_{\{ |f_n|\ge \lambda \}\cap\{ f_n \ge 0\} } |f_n| \,d\mu =0 を意味する。
証明終
ヴィタリの収束定理
定理2(ヴィタリの収束定理; Vitali convergence theorem)
(X,\mathcal{F},\mu) を測度空間,\color{red} \mu(X)<\infty とする。\{f_n\} は一様可積分で, f_n \xrightarrow {n\to\infty} f であるとき, f は可積分で,
\color{red} \lim_{n\to\infty} \int |f_n-f| \,d\mu = 0
である。特に,
が言える。
f_n \xrightarrow {n\to\infty} f は \mu\text{-a.e.} で構いません。
なお, \mu(X)<\infty の下で,ヴィタリの収束定理は,ルベーグの収束定理(DCT)より仮定が弱いです。実際, |f_n|\le F となる可積分関数 F が存在するとすると,
\begin{aligned}\sup_n \int_{|f_n|\ge \lambda} |f_n|\,d\mu &\le \int_{|F|\ge \lambda} |F|\,d\mu \\ &\xrightarrow[\text{DCT}]{\lambda\to\infty} 0\end{aligned}
より, \{f_n\} は自動的に一様可積分になりますね。
証明
Fatouの補題と定理1より, \int |f|\,d\mu\le \liminf_{n\to\infty} \int |f_n|\,d\mu\le\sup_n \int|f_n|\,d\mu<\infty であるから, f は可積分である。
\{f_n-f\} が一様可積分であることは,定理1を考えればわかる。 \varepsilon>0 とする。 \lambda>0 を十分大きくとることで, \sup_n\int_{\{|f_n-f|\ge \lambda\}}|f_n-f|\,d\mu<\varepsilon とする。すると,
\begin{aligned}&\int |f_n-f|\,d\mu \\ &\le \int_{\{|f_n-f|\ge \lambda\}}\!\!\!\!\!\!|f_n-f|\,d\mu + \int_{\{|f_n-f|<\lambda\}}\!\!\!\!\!\!|f_n-f|\,d\mu \\ &\le \varepsilon + \int_{\{|f_n-f|<\lambda\}}|f_n-f|\,d\mu. \end{aligned}
ここで, |f_n-f|1_{\{|f_n-f|<\lambda\}}\le \lambda であり,右辺は可積分であるから,ルベーグの収束定理(有界収束定理)より, n を十分大きくとると, \int_{\{|f_n-f|<\lambda\}}|f_n-f|\,d\mu<\varepsilon とできる。したがって,十分大きな n に対し,
であり,これより \lim_{n\to\infty}|f_n-f|\,d\mu =0 を得る。後半は明らか(分からなければルベーグの収束定理の証明の最終行の式を見よ)。
証明終
なお,定理2は逆も知られています。具体的には, \{f_n\},f が可積分で, f_n\xrightarrow{n\to\infty}f かつ \lim_{n\to\infty} \int |f_n-f| \,d\mu = 0 ならば, \{f_n\} は一様可積分です。証明は省略します。