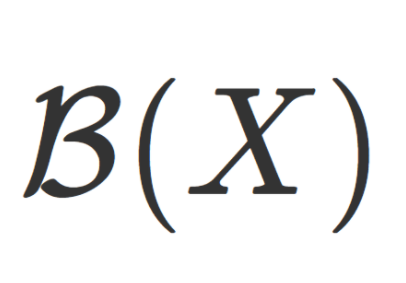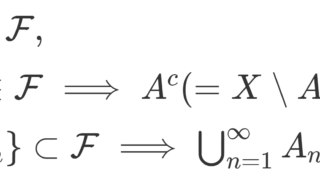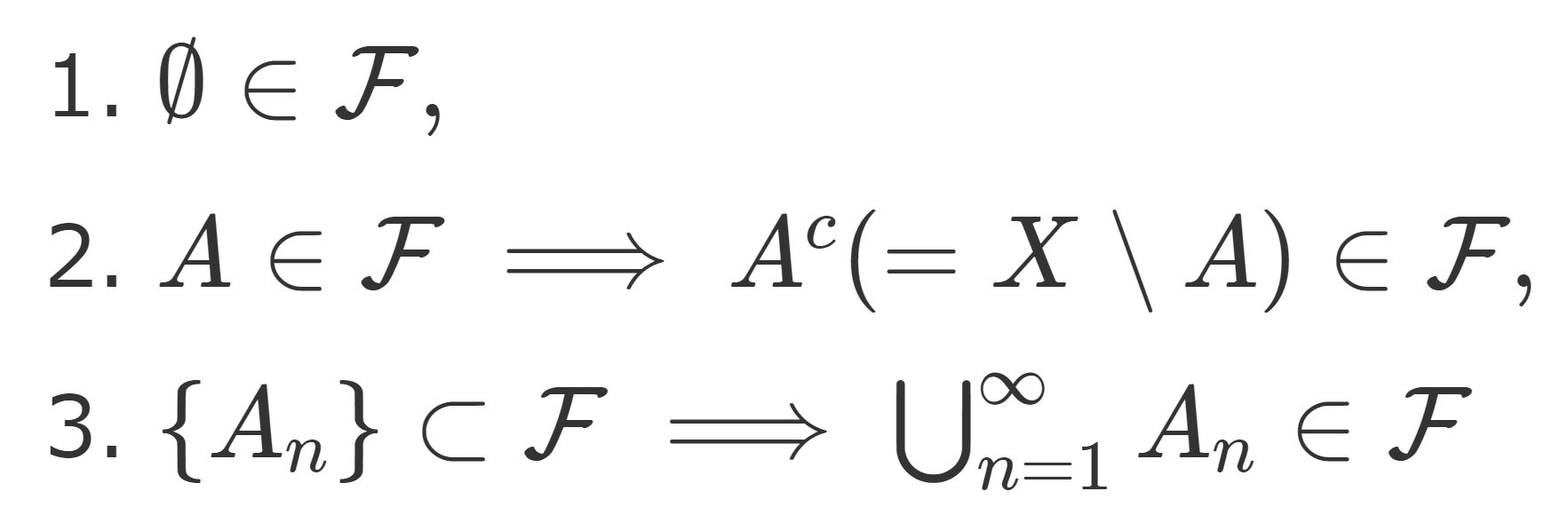ボレル集合とは,開集合から生成されるσ-加法族の元のことを言います。「生成される」とは,簡単に言うと「高々可算個の集合の共通部分・和集合・補集合・差集合を取る操作」を高々可算回,を高々可算回,を高々可算回……行うことです(厳密な説明ではありません)。
まずボレル集合の定義を述べ,それから実数上のボレル集合族は区間で生成されることを証明しましょう。
ボレル集合の定義
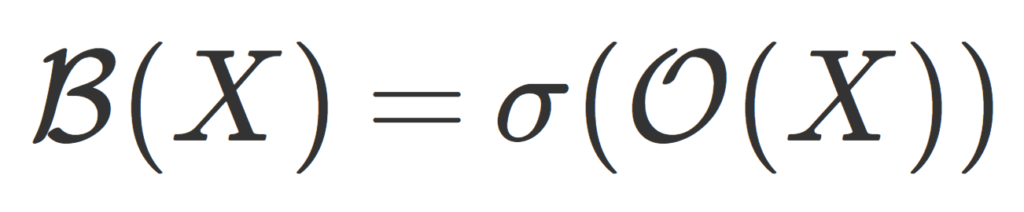
定義(ボレル集合)
(X,\mathcal{O}) を位相空間とする。このとき, X の開集合全体 \mathcal{O}(X) によって生成されるσ-加法族 (σ-field) をボレル集合族 (ボレル加法族,Borel field) といい, \color{red} \mathcal{B}(X)= \sigma(\mathcal{O}(X)) とかく。このときの \mathcal{B}(X) に属する集合をボレル集合 (Borel set) という。
σ-加法族のうち,位相空間の開集合系によって生成されるものをボレル集合族といい,その元をボレル集合というんですね。「生成される」とは,簡単に言うと「高々可算個の集合の共通部分・和集合・補集合・差集合を取る操作」を高々可算回行うことです。
なお, A\in \mathcal{B}(X)\implies A^c\in\mathcal{B}(X) ですから,全ての閉集合もボレル集合になります。逆に,全ての閉集合から生成されるσ-加法族も同じ \mathcal{B}(X) になります。
実数上のボレル集合
標準的な位相を備えた1次元ユークリッド空間 \mathbb{R} におけるボレル集合 \mathcal{B}(\mathbb{R})=\sigma(\mathcal{O}(\mathbb{R})) を考えましょう。
実数上のボレル集合の例
例(\mathcal{B}(\mathbb{R}) の例)
以下は全て \mathcal{B}(\mathbb{R}) におけるボレル集合である。
- (a,b) \quad (a<b )
- [a,b] \quad (a<b)
- [a,b)\quad (a<b)
- \{a\} \quad (a\in\mathbb{R})
- \mathbb{Q}
- \mathbb{R}\setminus \mathbb{Q}
1.は開集合ですからボレル集合で,2,4.は閉集合ですからボレル集合です。3.は [a,b) = \bigcup_{n=1}^\infty [a, b-1/n] とすれば,閉集合の可算和なのでボレル集合です。5.は4.と, \mathbb{Q} が一点集合の可算和であることからボレル集合です。6.は5.より \mathbb{Q}^c もボレル集合ですね。
特に \mathbb{Q} がボレル集合,すなわち「長さが測れる可測集合」であることは測度論における本質です。
実数上のボレル集合は区間で生成される
\mathbb{R} におけるボレル集合 \mathcal{B}(\mathbb{R})=\sigma(\mathcal{O}(\mathbb{R})) は,区間で生成されるσ-加法族です。具体的には以下の定理が成立します。
定理1( \mathbb{R} 上のボレル集合)
\begin{aligned}\mathfrak{A} &= \{ (a,b)\colon a<b,\, a,b \in\mathbb{Q}\}, \\ \mathfrak{B} &=\{ (a,b] \colon a<b,\, a,b\in \mathbb{Q}\},\\ \mathfrak{C} &= \{ [a,b) \colon a<b,\, a,b\in\mathbb{Q}\} , \\ \mathfrak{D} &= \{ [a,b]\colon a<b,\, a,b\in\mathbb{Q}\} ,\\ \mathfrak{E} &=\{ (-\infty, a) \colon a\in\mathbb{Q}\}, \\ \mathfrak{F} &= \{ (-\infty, a] \colon a\in\mathbb{Q}\}, \\ \mathfrak{G} &=\{ (a, \infty) \colon a\in\mathbb{Q}\}, \\ \mathfrak{H} &= \{ [a,\infty) \colon a\in\mathbb{Q}\} \end{aligned}
とする。このとき, \color{red} \sigma(\mathfrak{A})= \sigma(\mathfrak{B}) = \sigma(\mathfrak{C}) = \sigma(\mathfrak{D}) = \sigma(\mathfrak{E}) = \sigma(\mathfrak{F}) = \sigma(\mathfrak{G}) = \sigma(\mathfrak{H}) = \mathcal{B}(\mathbb{R}) である。
\mathbb{R} 上のボレル集合は区間で生成されるということですね。
証明
\sigma(\mathfrak{A})=\mathcal{B}(\mathbb{R}) について
\mathfrak{A}\subset \mathcal{O}(\mathbb{R}) より,両辺 \sigma(\cdot) を取って \sigma(\mathfrak{A})\subset \mathcal{B}(\mathbb{R}) は明らか。
U\in \mathcal{O}(\mathbb{R}) とする。開集合の定義と \mathbb{Q}\subset\mathbb{R} の稠密性より, x\in U に対し, x\in (a,b)\subset U となる a,b\in\mathbb{Q} が存在する。
U=\bigcup_{\substack{a,b \in\mathbb{Q}\\ (a,b)\subset U} } (a,b)
であるから,特に U\in \sigma(\mathfrak{A}) となるため, \mathcal{O}(\mathbb{R}) \subset \sigma(\mathfrak{A}) である。 両辺 \sigma(\cdot) を取って \mathcal{B}(\mathbb{R})\subset \sigma(\mathfrak{A}) となる。
\sigma(\mathfrak{A})=\sigma(\mathfrak{B}) について
(a,b] = \bigcap_{n=1}^\infty (a, b+\frac{1}{n}),\;\; (a,b) = \bigcup_{n=1}^\infty (a, b-\frac{1}{n}]
より, \mathfrak{B}\subset \sigma(\mathfrak{A}) かつ \mathfrak{A}\subset \sigma(\mathfrak{B}) である。両辺 \sigma(\cdot) を取って結論を得る。
\sigma(\mathfrak{B})=\sigma(\mathfrak{F}) について
\begin{aligned}(-\infty, b] &= \bigcup_{n=1}^\infty(-n,b],\quad \\(a,b] &= (-\infty, b] \setminus (-\infty, a]\end{aligned}
であることからわかる。
他はすべて同様なので省略する。
証明終
この定理は d 次元ユークリッド空間 \mathbb{R}^d に拡張できます。
定理2( \mathbb{R}^d 上のボレル集合)
\begin{aligned}\mathfrak{A}^d &= \bigl\{ (a_1,b_1)\times \dots\times (a_d,b_d)\colon a_i,b_i \in\mathbb{Q}\bigr\}, \\ \mathfrak{B}^d &=\bigl\{ (a_1,b_1]\times\dots\times (a_d,b_d] \colon a_i,b_i\in \mathbb{Q}\bigr\}\end{aligned}
とすると, \color{red} \sigma(\mathfrak{A}^d)= \sigma(\mathfrak{B}^d)=\mathcal{B}(\mathbb{R}^d) である。
全て述べるのは大変なので, [a_1, b_1)\times\dots\times [a_d,b_d) などの集合は省略しました。証明は U\subset \mathbb{R}^d を開集合としたときに
U=\bigcup_{\substack{a_i,b_i \in\mathbb{Q}\\ (a_1,b_1)\times \cdots \times (a_d,b_d)\subset U} } (a_1,b_1)\times \cdots \times (a_d,b_d)
とすれば,上の証明と同様にできます。さらに,この定理は以下に一般化されます。
定理(可分距離空間上のボレル集合)
(X,d) を可分距離空間,S\subset X をその可算稠密部分集合とする。
\begin{aligned} B(a,r) &= \{ x\in X\colon d(a,x)<r\} , \\ \mathfrak{A}&= \{ B(a,r) \colon a\in S, \, r\in\mathbb{Q}_{>0}\}\end{aligned}
とするとき, \color{red}\sigma(\mathfrak{A})=\mathcal{B}(X) である。
距離空間は位相空間であることに注意してください。証明は上と同様です。