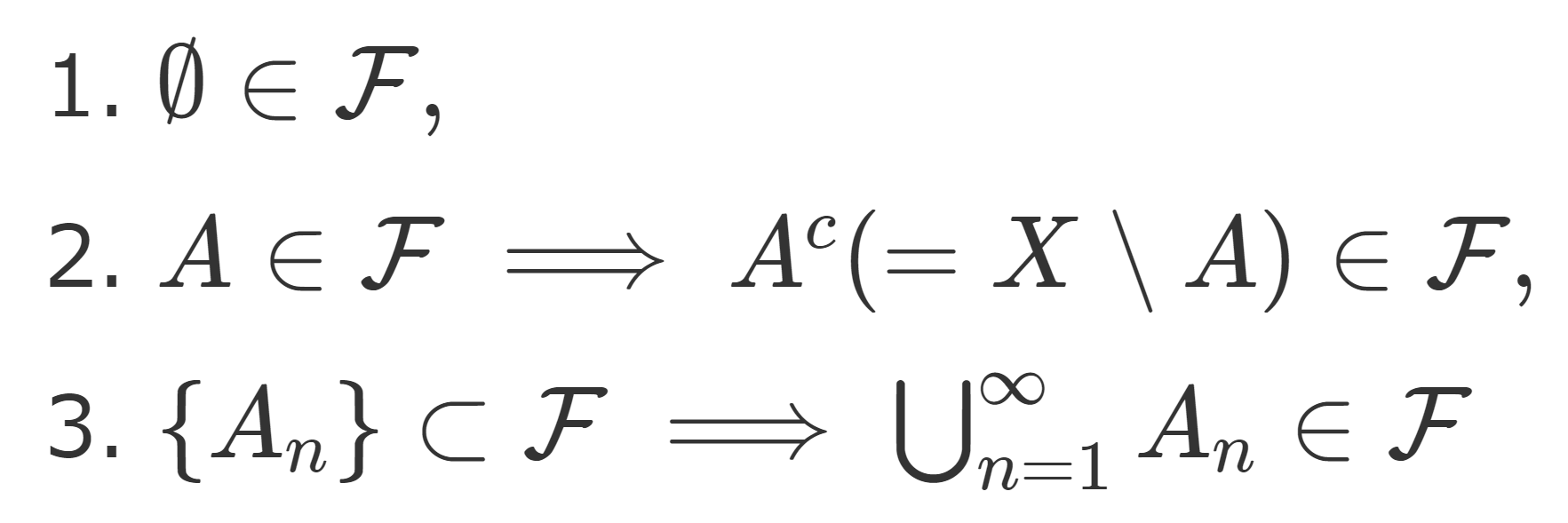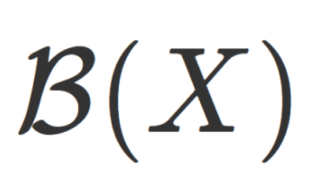解析学,特に測度論やルベーグ積分と呼ばれる分野における最も基本的な概念である,「σ-加法族」「可測空間」の定義とその基本的な性質について,丁寧に紹介していきましょう。
σ加法族・可測空間の定義とその意義
σ加法族・可測空間の定義
σはギリシャ文字の「シグマ」です。
定義(σ-加法族・可測空間・可測集合)
X を空でない集合とし, X の部分集合族 \mathcal{F}\subset 2^X (べき集合の部分集合)が
- \color{red}\emptyset \in \mathcal{F},
- \color{red}A\in\mathcal{F} \implies A^c (=X\setminus A)\in\mathcal{F},
- \color{red} \{A_n\}\subset \mathcal{F} \implies \bigcup_{n=1}^\infty A_n \in \mathcal{F}
をみたすとき, \mathcal{F} を X 上のσ-加法族(完全加法族,σ-代数,σ-field,σ-algebra)という。このとき, (X, \mathcal{F}) を可測空間 (measurable space) といい, \mathcal{F} の各元を可測集合 (measurable set) という。
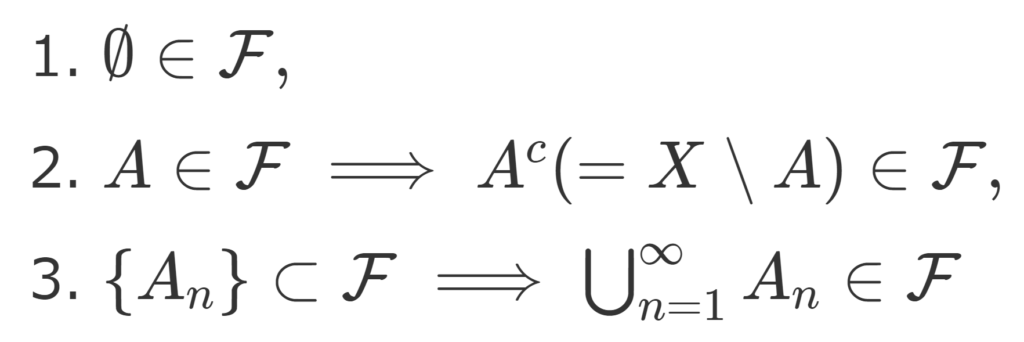
\mathcal{F} の性質2.を補集合について閉じている,性質3.を可算個の和について閉じているといいます。ここで大事なのは「可算個」であるということです。有限個では不足ですし,逆に非可算個の和について閉じていることは課しません。「σ」とは可算を意味します。
なお, A_k=A_{k+1}=\dots として性質3.を適用することで, A_1, A_2,\dots ,A_k \in \mathcal{F} \implies A_1 \cup A_2\cup \dots \cup A_k \in\mathcal{F} も言えます。すなわち,有限個の和について閉じていることも言えます。
定義の3.の代わりに, A_1 ,A_2,\dots, A_k \in\mathcal{F} \implies A_1\cup A_2 \cup \dots \cup A_k \in\mathcal{F} を仮定したものを有限加法族といいます。 \mathcal{F} がσ-加法族ならば有限加法族です。
σ加法族・可測空間の意義
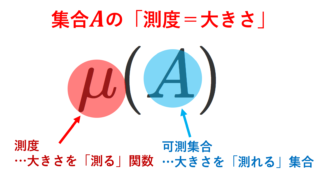
σ-加法族なんて考えて何の意味があるの? って思ったかもしれません。「σ-加法族」とは,あとで「測度」という概念を導入することで,大きさの測れる集合たちになります。「大きさ」とは「長さ」とか「面積」とか「体積」のことです。
測度とは,σ-加法族を定義域とし,非負の実数値を返す「いい感じの性質を持つ」写像です。これを導入することで,σ-加法族の元の「大きさ」が測れるようになります。要するに「長さ」とかの概念の一般化です。
σ-加法族の元を「可測集合」といいますが,「大きさを測ることが可能」という意味です。
σ-加法族そのものが重要というよりは,その上に「大きさ」が定まるということが大事です。そして,「いい感じの大きさ」を定めるためには,どうしても定義にある3つの性質が必要なのです。
σ加法族の具体例
σ-加法族の具体例を挙げましょう。
例1.
X=\{ a,b,c\} とする。このとき,
\mathcal{F} =\bigl\{ \emptyset, \{ a\}, \{b,c\} , X \bigr\}
はσ-加法族である。
定義をみたしているかは演習問題としましょう。
例2.
X=\{ a,b,c,d\} とする。このとき,
\begin{aligned}\mathcal{F} = \bigl\{ &\emptyset, \{ a\}, \{b\},\{a,b\}, \\ &\{c,d\}, \{a,c,d\} ,\{b,c,d\} , X \bigr\}\end{aligned}
はσ-加法族である。
有限集合であれば,σ-加法族であることと,有限加法族であることは一致します。
例3.
X を空でない集合とする。このとき, \mathcal{F} = \{ \emptyset, X \} はσ-加法族である。また, \mathcal{F}' = 2^X (べき集合)もσ-加法族である。
\mathcal{F}=\{\emptyset, X\} もσ-加法族ですが,この上に「大きさ」を定めてもあんまり意味がない感じがしますね。
逆に, \mathcal{F} = 2^X も当然σ-加法族の定義をみたします。もちろん,このうえに「いい感じの大きさ」を定めることができれば非常にありがたいですが,そもそもそんなことが可能かという問題があります。
\mathcal{F} にたくさんの集合が含まれていれば,それだけその上に「いい感じの大きさ」を定めるのは難しくなります。(もちろん,全ての「大きさ」が 0 になるようなものなら定めることは可能ですが。)
σ加法族の性質
以下は覚えておくべき性質です。
定理1(σ-加法族の性質1)
\mathcal{F} を集合 X 上のσ-加法族とするとき,
- X\in\mathcal{F}.
- \{A_n \}\in\mathcal{F} \implies \bigcap_{n=1}^\infty A_n \in\mathcal{F}.
- A, B\in\mathcal{F} \implies A\setminus B \in \mathcal{F}.
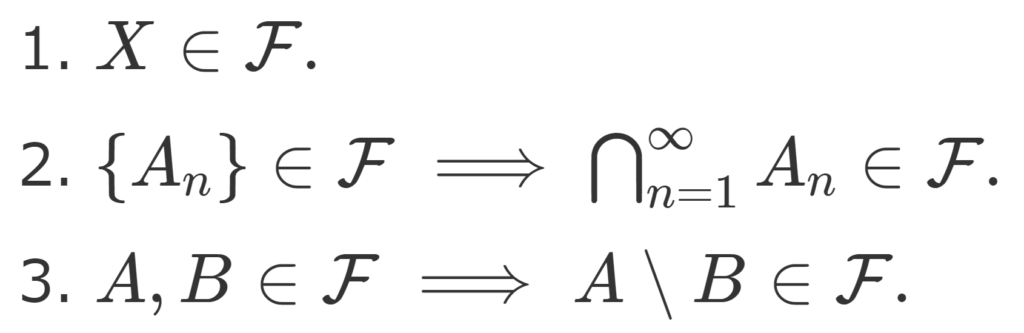
可算個の和について閉じているだけでなく,可算個の共通部分に関しても閉じていることが言えます。これは非常に大事です。
なお,2.を A_k =A_{k+1} = \dots として適用することで, A_1, A_2,\dots, A_k \in\mathcal{F} \implies A_1 \cap A_2 \cap\dots \cap A_k \in\mathcal{F} も分かります。すなわち,有限個の共通部分についても閉じています。
証明
1. X\in\mathcal{F} について
\emptyset \in \mathcal{F} \implies X = \emptyset^c \in \mathcal{F} より。
2. \{A_n\}\in\mathcal{F}\implies \bigcap_{n=1}^\infty A_n \in\mathcal{F} について
\{A_n \}\subset\mathcal{F} とすると, \{A_n^c\}\subset\mathcal{F} である。よって,
\left(\bigcap_{n=1}^\infty A_n\right)^c = \bigcup_{n=1}^\infty A_n^c \in\mathcal{F}
であるため,補集合を考えて \bigcap_{n=1}^\infty A_n \in \mathcal{F} である。
3. A,B\in\mathcal{F}\implies A\setminus B\in\mathcal{F} について
B\in\mathcal{F} より B^c\in\mathcal{F} であり, A\setminus B = A\cap B^c \in\mathcal{F} である。
証明終
もう一つ定理を紹介しましょう。
定理2(σ-加法族の性質2)
\{\mathcal{F}_\lambda\}_{\lambda\in\Lambda} を集合 X 上のσ-加法族の族とする。このとき, \color{red}\mathcal{F}=\bigcap_{\lambda\in\Lambda} \mathcal{F}_\lambda も X 上のσ-加法族である。
です。
証明
全ての \lambda\in\Lambda について \emptyset \in \mathcal{F}_\lambda より, \emptyset \in \bigcap_{\lambda\in\Lambda} \mathcal{F}_\lambda である。
A\in\bigcap_{\lambda\in\Lambda} \mathcal{F}_\lambda とすると,任意の \lambda\in\Lambda に対して A\in \mathcal{F}_\lambda なので, A^c\in\mathcal{F}_\lambda である。よって, A^c\in \bigcap_{\lambda\in\Lambda} \mathcal{F}_\lambda である。
\{A_n\} \subset \bigcap_{\lambda\in\Lambda} \mathcal{F}_\lambda \implies \bigcup_{n=1}^\infty A_n \in \bigcap_{\lambda\in\Lambda} \mathcal{F}_\lambda も同様。
証明終
なお,逆に \bigcup_{\lambda\in\Lambda} \mathcal{F}_\lambda はσ-加法族とは言えません。たとえば, X=\{a,b,c,d,e\} に対して,
\begin{aligned}\mathcal{F}_1 &=\bigl\{ \emptyset , \{a\}, \{b,c,d,e\}, X\bigr\},\\ \mathcal{F}_2 &=\bigl\{\emptyset, \{e\}, \{a,b,c,d\}, X\bigr\} \end{aligned}
とすると, \mathcal{F}_1 \cup \mathcal{F}_2=\bigl\{\emptyset,\{a\}, \{e\}, \{a,b,c,d\}, \{b,c,d,e\}, X \bigr\} はσ-加法族ではありません。
σ加法族の生成
定義(σ-加法族の生成)
X を空でない集合, F\subset 2^X をその部分集合族とする。このとき, F の元をすべて含む最小のσ-加法族が存在する。これを \color{red} \sigma(F) とかき, F によって生成されるσ-加法族という。
F 自体はただの集合族で,σ-加法族でなくて構いません。
「最小のσ-加法族の存在」は次のようにして分かります。まず,
\mathscr{F} = \{ \mathcal{F}\supset F \mid \mathcal{F} \text{ is } \sigma \text{-field}\}
を F を含むσ-加法族の集合としましょう。 2^X\in \mathscr{F} ですから,これは空ではありません。このとき,
も定理2よりσ-加法族です。特に, F を含む最小のσ-加法族です。よって, \sigma (F) = \mathcal{F}_0 としてあげればよいですね。
\sigma(\{a\}) のときは省略して \sigma(a) とかきます。具体例を挙げましょう。
例4.
X=\{a,b,c,d\} に対し,
\begin{aligned}\sigma(a) &= \{ \emptyset, \{a\}, \{b,c,d\} , X\},\\ \sigma(\{a,b\}) &= \{ \emptyset , \{a,b\}, \{c,d\}, X\} .\end{aligned}「生成される」とは,簡単に言うと「高々可算個の集合の共通部分・和集合・補集合・差集合を取る操作」を高々可算回,を高々可算回,を高々可算回……行うことです(厳密な説明ではありません)。
なお,位相空間において,開集合から生成されるσ-加法族をボレル加法族(ボレル集合族)といいます。これについては,以下で掘り下げています。