専門数学を理解するにあたって重要な概念の一つの「無限の大小」について,すなわち可算集合(可算無限)と非可算集合(非可算無限)について,その定義と性質を紹介しましょう。非可算集合については,連続体濃度を扱います。
可算集合と非可算集合(可算無限・非可算無限)
集合 A の濃度を |A| で表すことにしましょう。
定義(可算集合・非可算集合)
\mathbb{N}=\{1,2,3,\ldots\} を正の整数全体の集合とする。
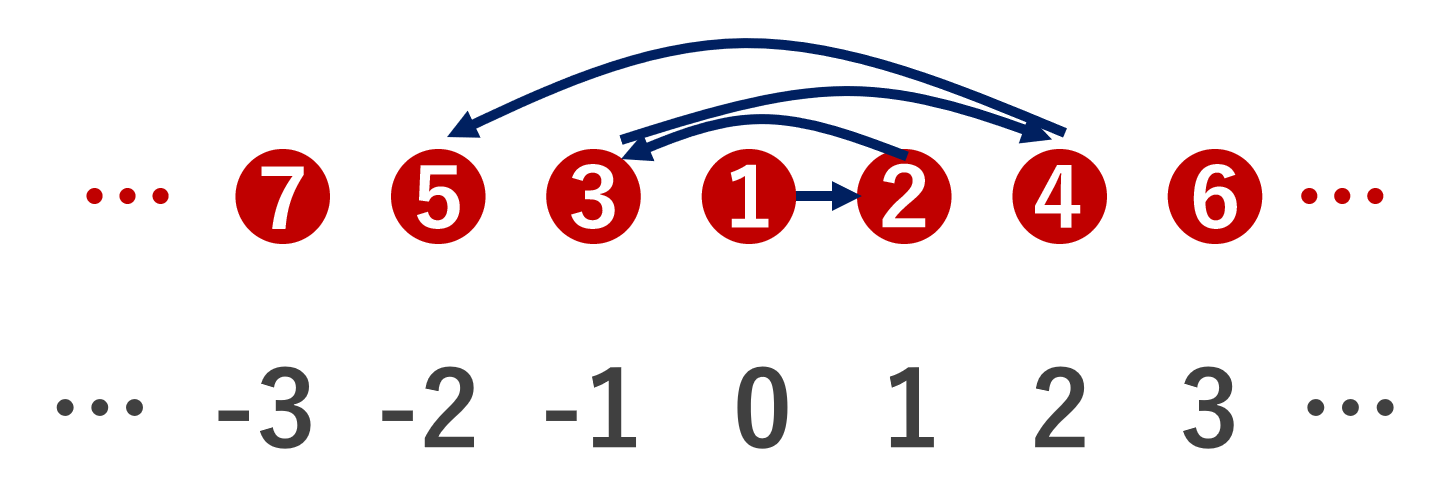
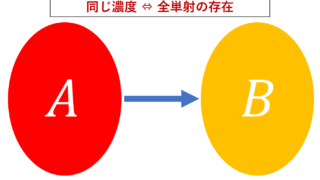
- 集合 A の濃度に関し,\color{red} |\mathbb{N}| =|A|,すなわち全単射 f\colon \mathbb{N} \to A が存在するとき, A は可算集合 (countable set) であるといい, A の濃度は可算無限(可算濃度)であるという。
- 集合 A が可算集合でない無限集合のとき,非可算集合 (uncountable set) であるといい,A の濃度は非可算無限(非可算濃度)であるという。
可算濃度を |\mathbb{N}| = \textcolor{red}{\aleph_0} (アレフゼロ)とかくことがある。
正の整数と同じ濃度のものかどうか,違うかどうかで,「可算集合」「非可算集合」という言葉の使い分けをするんですね。「可算」とは「数えられる」,すなわち \mathbb{N} との全単射で「番号が振れる」という意味です。
有限集合と可算集合を合わせて,高々可算集合という言葉もあります。
ここで,集合の濃度に関する知識は,可算集合・非可算集合を理解するうえで必須です.上の定義が分からなかった場合は,まずは「集合の濃度」の理解からするとよいでしょう。以下の記事を参照してください。
可算集合(可算無限)について
可算集合,すなわち, \mathbb{N}= \{ 1,2,3,\ldots\} と同じ濃度である集合,さらに言い換えると, \mathbb{N} と全単射が作れる集合について考えましょう。
可算集合の具体例とその証明
定理(可算集合の具体例)
以下の集合は全て可算集合である。
- \color{red} a\mathbb{N}= \{a,2a, 3a,\ldots\} \;(a\ne 0)
- \color{red} \mathbb{Z} (整数全体の集合)
- \color{red} \mathbb{N}^m =\{ (a_1,a_2,\dots, a_m)\mid a_j \in \mathbb{N}\},ただし, m は正の整数
- \color{red} \mathbb{Q} (有理数全体の集合)
- 代数的数,すなわち \color{red}\{ x\in \mathbb{C} \mid a_nx^n + \cdots + a_1x +a_0 = 0, \; a_j \in \mathbb{Q}\;, n\ge 1\}
早速証明しましょう。もう一度おさらいすると, \mathbb{N} と同じ濃度とは, \mathbb{N} との全単射が存在することでした。
証明
1. a\mathbb{N}= \{a,2a, 3a,\ldots\} \;(a\ne 0) について
f(n) = an とすると, f\colon \mathbb{N} \to a\mathbb{N} は全単射である。
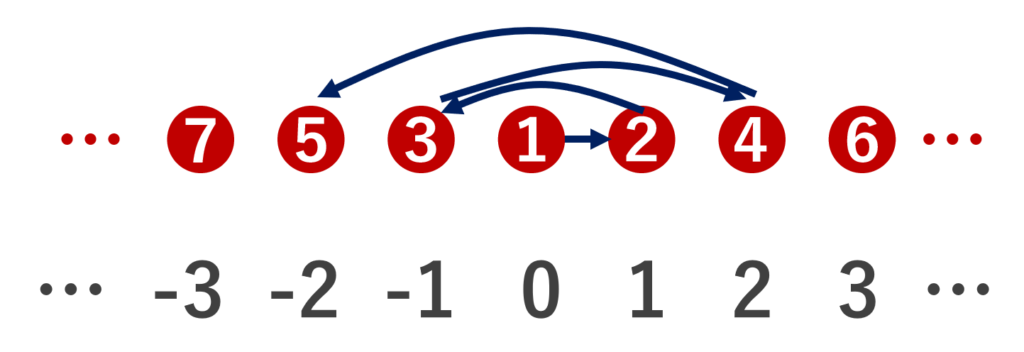
2. \mathbb{Z} (整数全体の集合)について
f(n) = \begin{cases} k & n=2k \; (k=1,2,\ldots) \\ -k & n=2k+1 \;(k=0,1,2,\ldots) \end{cases} とすると, f\colon \mathbb{N}\to\mathbb{Z} は全単射である。
3. \mathbb{N}^m =\{ (a_1,a_2,\dots, a_m)\mid a_j \in \mathbb{N}\} について
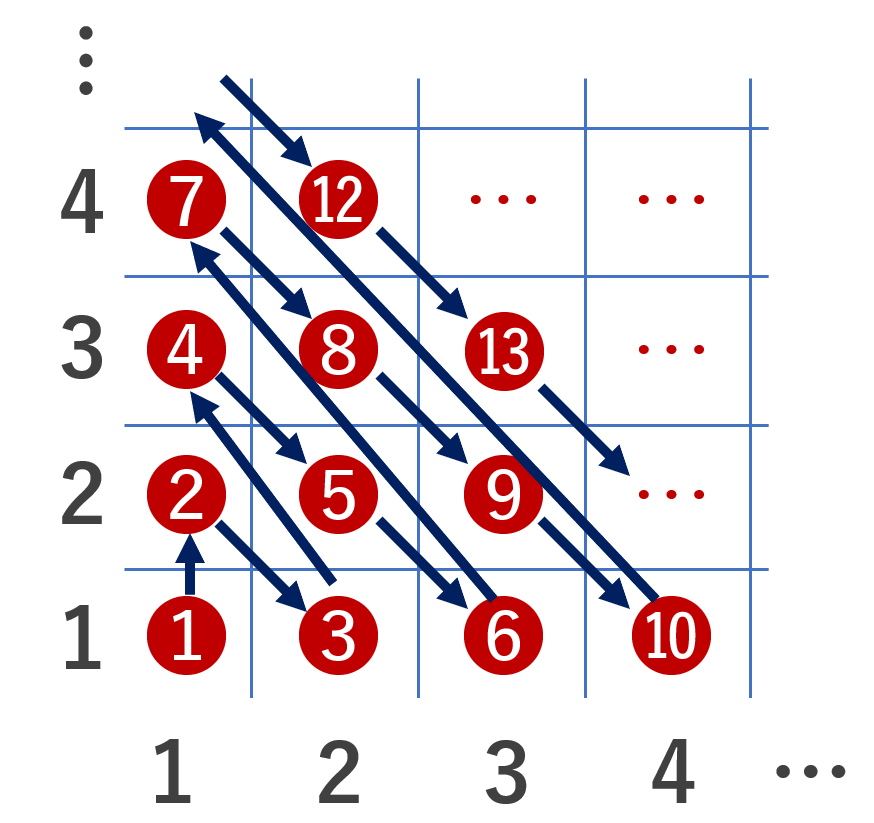
m=2 の場合で示せば,帰納法により十分である。実際,全単射 f_1 \colon \mathbb{N}\times \mathbb{N} \to \mathbb{N} が構成できれば, f_2(l,m,n) = f_1(f_1(l,m),n) と定めることで,f_2\colon \mathbb{N}\times\mathbb{N}\times\mathbb{N} \to\mathbb{N} は全単射になるからである。
全単射 f\colon \mathbb{N}\times\mathbb{N}\to \mathbb{N} を構成しよう。これは,たとえば f(m,n) = m+(m+n-1)(m+n-2) /2 とすればよい。
4. \mathbb{Q} (有理数全体の集合)について
\mathbb{N}\subset \mathbb{Q} であるから, |\mathbb{N}|\le |\mathbb{Q}| である。一方で,既約分数 p/q ( p,q は整数) に対して写像 p/q \mapsto (p,q ) \in \mathbb{Z}\times \mathbb{N} を考えると,これは単射であるから, |\mathbb{Q}|\le |\mathbb{Z}\times \mathbb{N} | も分かる。3.より, |\mathbb{N}| =| \mathbb{N}\times \mathbb{N}|=|\mathbb{Z}\times \mathbb{N}| であったから,
|\mathbb{N}| = |\mathbb{Q}| = | \mathbb{N}\times \mathbb{N}| が従う。
5. 代数的数,すなわち \{ x\in \mathbb{C} \mid a_nx^n + \cdots + a_1x +a_0 = 0, \; a_j \in \mathbb{Q}\;, n\ge 1, a_n\ne 0\} について
m\ge 1 を整数とする。 A_m = \{ x\in \mathbb{C}\mid a_mx^m+\cdots +a_1x+a_0 = 0, a_j \in\mathbb{Q}, a_m \ne 0\} と定めると,この濃度は m 次の方程式全体の集合の濃度以下である。特に \mathbb{N} \subset A_m も踏まえると,
|\mathbb{N}|\le |A_m| \le | \mathbb{ Q}^m |
となる。4.と次節の定理1.より, |\mathbb{Q}^m| = |\mathbb{N}| なので, A_m は可算集合である。
求める集合を A とすると, A = \bigcup_{m\ge 1} A_m である。これは,次節の定理3.より,可算集合である(ただし,ここでは数の具体的な性質をうまく使うことにより,選択公理は必要ない)。
証明終
4.は,「既約分数でないものを飛ばして3.のように番号付けする」と思っても構いません。
以上から, |\mathbb{N}| = |\mathbb{Z}| = |\mathbb{Q}| が分かりましたね。ちなみに,実数全体の集合 \mathbb{R} は可算集合ではありません。実際,
|\mathbb{N}| = |\mathbb{Z}| = |\mathbb{Q}|<|\mathbb{R}| = |\mathbb{C}|
となります。実数全体の集合の濃度については,後で扱いましょう。
可算集合のより一般的な性質
ここでは,上のことも踏まえて,より一般的な性質について述べましょう。
定理(可算集合の一般的な性質)
- 可算集合の有限個の直積は可算集合である。
- 可算集合のべき集合は非可算集合である。
- \{A_n\} を可算集合の列とする。このとき,\displaystyle \color{red}A=\bigcup_{n=1}^\infty A_n も可算集合である(選択公理が必要)。
1.の証明は, |\mathbb{N} \times \mathbb{N} | = |\mathbb{N}| を使えばよいです。 A, B を可算集合としたとき,その直積は全単射
A\times B \to \mathbb{N} \times \mathbb{N} \to \mathbb{N}
を構成することで, A\times B が可算集合だとわかります。
ここでは,3.のみ証明しましょう。3.の証明には,選択公理と呼ばれる公理が必要です。選択公理については,もう一段深い知識が必要ですから,分からなければ「おまじない」という認識で良いです。
3.の証明
\{ A_n \} は互いに素であるとする。すなわち, i\ne j \implies A_i \cap A_j =\emptyset とする。各 A_n は可算集合であるから,その要素を番号付けて \{ a_{n,k}\}_k とできる。このとき, A の要素は, \{a_{n,k}\}_{n,k} である。
この濃度は, \{(n,k) \}_{n,k} の濃度,すなわち |\mathbb{N}\times \mathbb{N}| に一致する。 |\mathbb{N}\times \mathbb{N}| = |\mathbb{N} | はすでに示したから, A は可算濃度である。
\{A_n\} が互いに素でないとき,上の計算では,重複して数えている要素があることになる。これより A は高々可算集合である。 A_1\subset A は可算集合であるから,結局, A は可算集合である。
証明終
各集合 A_n を, \{ a_{n,k}\}_k と番号付けしていますが,番号付けの仕方は何通りもあり,「選択」が必要です。 F_n を A_n の番号付けの仕方全体(F_n=\{ f\colon \mathbb{N}\to A_n \text{: bijection}\} , bijection は全単射の意味)とすると,これは
( \{a_{n,k}\}_k)_n \in \prod_{n=1}^\infty F_n
とできると言っていますから,選択公理が必要です(→選択公理の内容と具体例を詳しく)。
非可算集合(非可算無限)について
非可算集合について紹介しましょう。選択公理を仮定すると,任意の非可算濃度は可算濃度よりも必ず大きくなることが知られています(→選択公理の内容と具体例を詳しく)。
今回は,非可算濃度で最も代表的な「連続体濃度」について紹介しましょう。
連続体濃度
定義(連続体濃度)
集合 A の濃度に関し, \color{red}|\mathbb{R}| = |A| ,すなわち全単射 f\colon \mathbb{R}\to A が存在するとき, A は連続体濃度 (cardinality of the continuum) であるという。
連続体濃度を |\mathbb{R}| = \textcolor{red}{\aleph} (アレフ)とかくことがある。
\mathbb{R} は可算濃度でない,すなわち, |\mathbb{N}|<|\mathbb{R}| であることが知られています(→カントールの対角線論法とそれを用いた証明)。
連続体濃度と同じ濃度であるものの例を挙げましょう。
定理(連続体濃度の具体例)
以下の集合の濃度は全て連続体濃度である。
- \color{red}(0,1)
- \color{red}[0,1]
- \color{red}\mathbb{C}
- \color{red} \mathbb{R}^n
- べき集合 \color{red}2^\mathbb{N}
- カントールの三進集合
ここでは,1,2.のみ証明します。
1-2.の証明
f(x) = \tan (\pi x-\pi/2) とすると, f\colon (0,1)\to \mathbb{R} は全単射である。また,
g(x)=\begin{cases} 1/2 & x=0, \\ 1/2^{k+2} & x=1/2^k \; (k=0,1,2,\ldots), \\ x & \text{otherwise} \end{cases}
とすると, g\colon [0,1] \to (0,1) は全単射である。従って,
がわかる。
証明終
他に,6.の証明はカントール集合の定義と性質3つの証明の中で行っています。