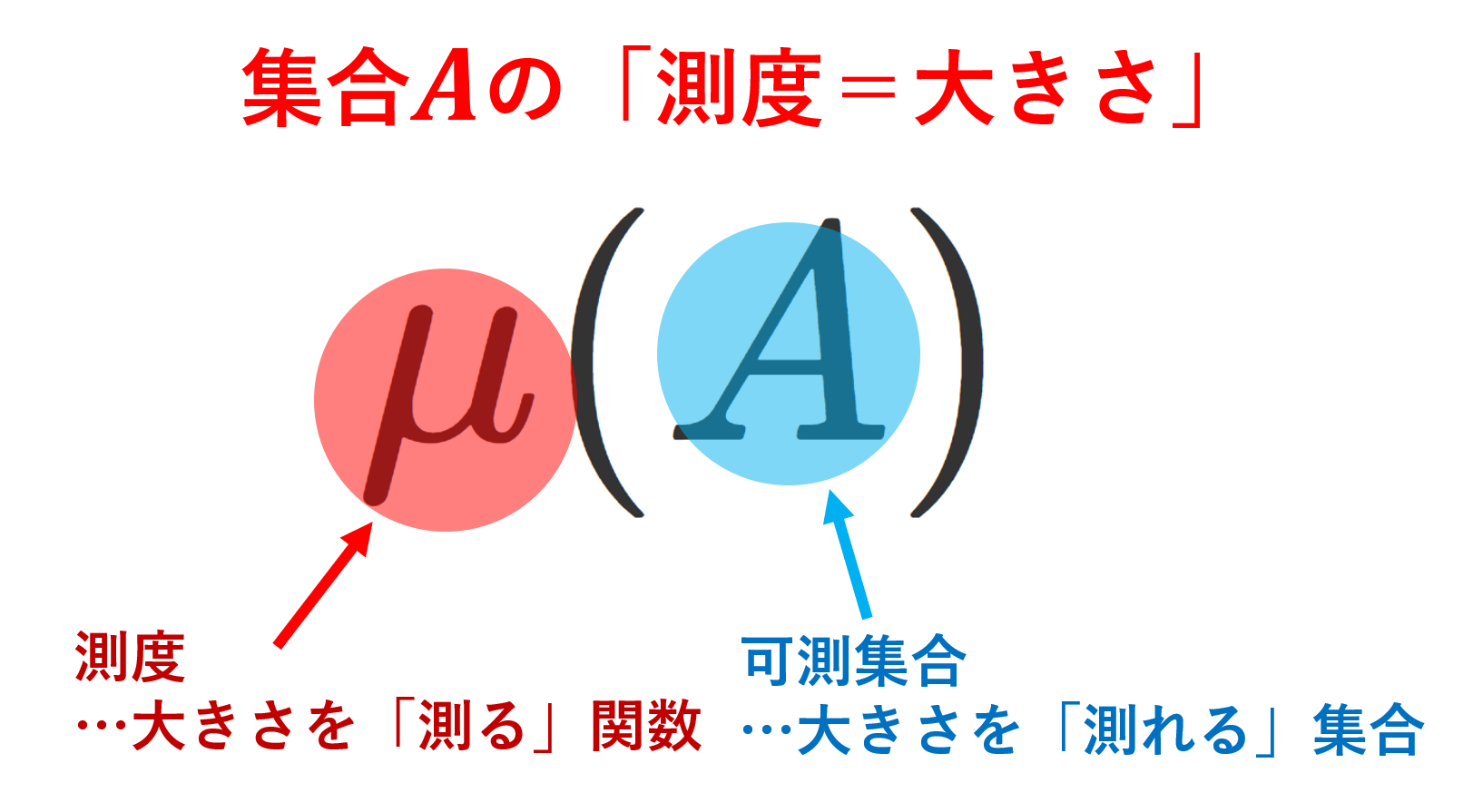
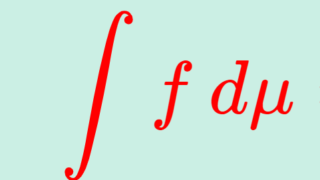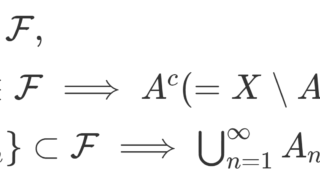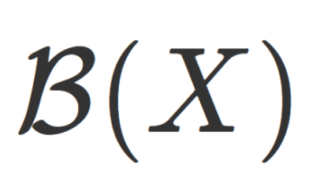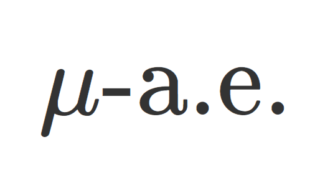測度論の基盤である「測度」について,その定義と具体例4つ・基本的な性質5つを順番に解説していきましょう。どれも測度論の最も基本的な概念ですから,しっかり理解していきましょう。
可測空間・可測集合の概念は既知とします(→σ加法族と可測空間の定義・基本的な性質をわかりやすく)。
測度・測度空間の定義
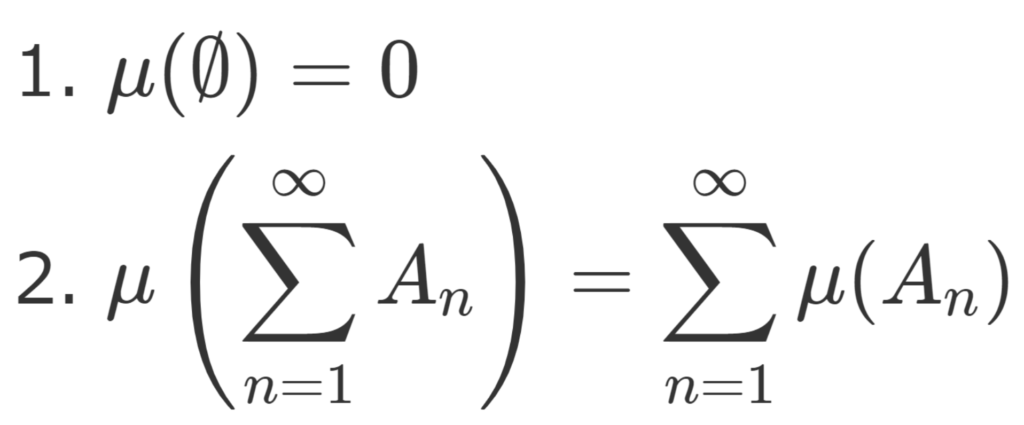
定義(測度・測度空間)
(X,\mathcal{F}) を可測空間とする。関数 \mu \colon \mathcal{F}\to [0,\infty] が (X,\mathcal{F}) 上の測度 (measure) であるとは,
- \color{red} \mu(\emptyset) = 0
- \{A_n\}\subset\mathcal{F} をどの2つも互いに素とするとき, \displaystyle \color{red} \mu\left(\sum_{n=1}^\infty A_n\right) = \sum_{n=1}^\infty \mu (A_n) (可算加法性)
の両方が成立することを言う。このときの (X,\mathcal{F},\mu) を測度空間 (measure space) といい,可測集合 A\in\mathcal{F} に対し, \mu(A) を A の測度という。
ただし,集合列 \{A_n\} がどの2つも「互いに素 (disjoint)」とは,i\ne j\implies A_i\cap A_j =\emptyset を指し, \sum_{n=1}^\infty A_n =\bigcup_{n=1}^\infty A_n である(特に非交和のときに左辺の記号を用いる)。
まず注意として,σ-加法族の定義から \emptyset \in\mathcal{F} や \{A_n\}\subset \mathcal{F} \implies \bigcup_{n=1}^\infty A_n\in\mathcal{F} が成立することに注意しましょう。よって,1.や2.の左辺は定義可能です。2.については,両辺 \infty となる可能性もあります。
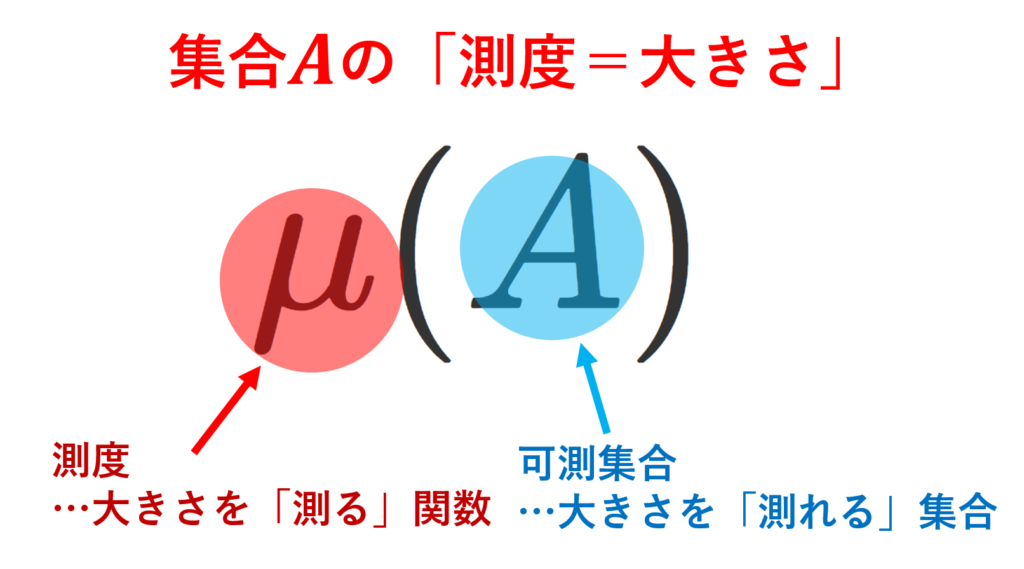
測度は,測度論における最も基本的なもののひとつで,集合の「大きさ」を測るのに用いるものです。 \mu(A) を集合 A の大きさと考えるわけです。測度の定義に出てくる2つの性質は「大きさを測るのに成り立ってほしい都合の良い性質」です。
なお,測度空間 (X,\mathcal{F},\mu) に対して, \mu(A)=0 となる集合 A\in\mathcal{F} を零集合 (null set) といいます。 測度論においては,零集合上の違いを無視することが多いです(→ほとんどいたるところ(almost everywhere, a.e.)の議論)。
測度の具体例4つ
例1(零測度).
可測空間 (X,\mathcal{F}) に対し, \color{red}\mu_0 (A) = 0\;\, (A\in\mathcal{F}) とすると, \mu_0 \colon \mathcal{F}\to \{0\} \subset [0,\infty] は測度となる。これを零測度 (null measure) という。
すべての集合が測度 0 になるような測度ですね。すべての集合が零集合になります。
例2(数え上げ測度).
可測空間 (X,\mathcal{F}) に対し, \# \colon \mathcal{F}\to \mathbb{Z}_{\ge 0} \cup \{\infty\} \subset [0,\infty] を集合の要素の個数 \color{red} \#(A) を返す写像とすると,これは測度となる。これを数え上げ測度 (counting measure) という。
\# は集合の要素の個数を表すもので,たとえば \#(\emptyset) = 0,\; \#(\{a,b,c\}) = 3,\; \#(\mathbb{R}) = \infty となります。
測度になることは容易に確認できるでしょう。
例3(ディラック測度・デルタ測度).
可測空間 (X,\mathcal{F}) に対し, \{x\}\in \mathcal{F} とする。 このとき, A\in\mathcal{F} に対し
\color{red} \delta_x(A) = \begin{cases} 1 & x\in A, \\ 0& x\in X\setminus A \end{cases}
となる測度をディラック測度 (Dirac measure) またはデルタ測度 (Delta measure) という。
定義関数(指示関数)を用いると, \delta_x(A)=1_A(x) とも書けますね。1点のみに「重み」をもつ測度です。
可算個の「可測1点集合」に正の測度を持つ測度は \{a_n\} \subset X ,\; \{k_n\}\subset \mathbb{R}_{>0} を用いて \mu = \sum_{n=1}^\infty k_n \delta_{a_n} と記述できます。
例4(ルベーグ測度).
ボレル可測空間 (\mathbb{R}, \mathcal{B}(\mathbb{R})) に対して,
\color{red} \operatorname{Leb}([a,b]) = \operatorname{Leb}((a,b))=b-a
となるような測度 \operatorname{Leb} \colon \mathcal{B}(\mathbb{R})\to [0,\infty] は一意的に存在する。これをルベーグ測度 (Lebesgue measure) という。
ルベーグ測度の存在と一意性は一つの大きな問題です。
測度とは,集合の大きさを定めるものであることを端的に示すのが,この具体例でしょう。区間 [a,b] や (a,b) の「大きさ」が b-a と言っているわけです。
測度の性質5つとその証明
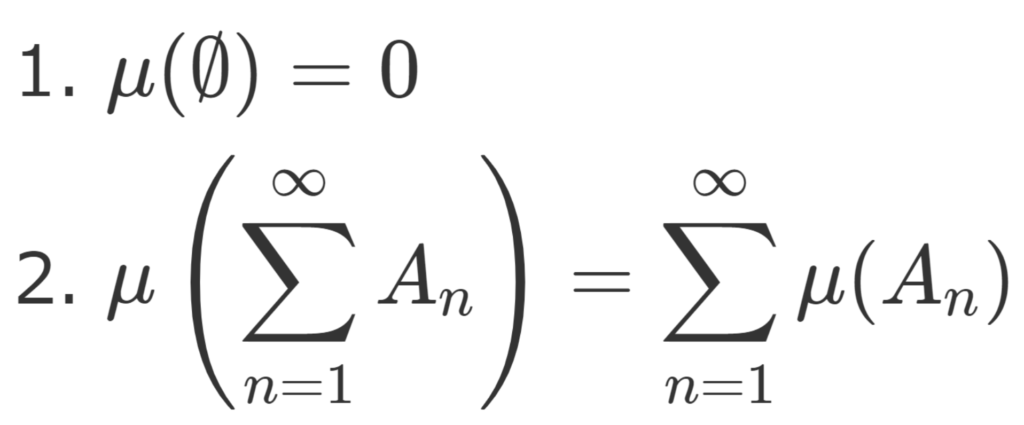
定理(測度の性質)
(X,\mathcal{F},\mu) を測度空間とする。このとき,
- \{A_n\}_{n=1}^m\subset\mathcal{F} がどの2つも互いに素ならば, \mu(\sum_{n=1}^m A_n) = \sum_{n=1}^m \mu(A_n) (有限加法性)
- A,B\in\mathcal{F} に対し,A\subset B,\; \mu(A)<\infty ならば,\mu(B\setminus A) = \mu(B)-\mu(A) である。特に \mu(A)\le \mu(B) である(単調性)。
- \{A_n\}\subset\mathcal{F} とする(互いに素でなくてもよい)とき,\mu\bigl(\bigcup_{n=1}^\infty A_n\bigr) \le \sum_{n=1}^\infty \mu(A_n) (劣加法性)
- \{A_n\}\subset\mathcal{F} かつ A_n\uparrow A とするとき, \mu(A_n)\uparrow \mu(A) である。
- \{A_n\}\subset\mathcal{F} かつ \mu(A_n)<\infty かつ A_n\downarrow A とするとき, \mu(A_n)\downarrow \mu(A) である。
4.について, A_n \uparrow A とは A_1\subset A_2\subset A_3\subset \cdots かつ A=\bigcup_{n=1}^\infty A_n を指し, \mu(A_n)\uparrow \mu(A) とは \mu(A_1)\le \mu(A_2)\le \mu(A_3)\le \cdots かつ \mu(A_n)\to \mu(A) を意味します。 A \in \mathcal{F} は仮定していませんが,従うことに注意してください。
5.における A_n\downarrow A,\; \mu(A_n)\downarrow\mu(A) の定義もほぼ同様です。
すべて基本的な性質です。証明もしっかり理解しましょう。
1. 有限加法性について
1. \{A_n\}_{n=1}^m\subset \mathcal{F} がどの2つも互いに素ならば, \mu(\sum_{n=1}^m A_n) = \sum_{n=1}^m \mu(A_n) (有限加法性)
どの2つも互いに素とは, i\ne j\implies A_i\cap A_j =\emptyset でした。
証明
A_{m+1}=A_{m+2}=\dots = \emptyset として,可算加法性を用いればよい。
証明終
2. μ(B-A) = μ(B)-μ(A) について
2. A,B\in\mathcal{F} が A\subset B, \mu(A)<\infty ならば,\mu(B\setminus A)=\mu(B)-\mu(A) である。 特に \mu(A)\le \mu(B) である(単調性)。
\mu(A)<\infty を仮定したのは,\infty -\infty とならないためであり, \mu(A)\le \mu(B) 自体は \mu(A)=\infty でも成立します。
証明
有限加法性(1.)と B =A +B\setminus A (右辺の2つは互いに素) から,
\mu(B) = \mu(A) +\mu(B \setminus A).
特に \mu(A)\le \mu(B) である。 \mu(A)<\infty なら両辺 \mu(A) を引いて \mu(B\setminus A)=\mu(B)-\mu(A) である。
証明終
3. 劣加法性について
3. \{A_n\}\subset\mathcal{F} とするとき, \mu\bigl(\bigcup_{n=1}^\infty A_n\bigr) \le \sum_{n=1}^\infty \mu(A_n) (劣加法性)
証明
B_1 = A_1 と m\ge 2 に対して B_m = A_m \setminus\bigcup_{n=1}^{m-1} A_n とする。すると, \{B_n\} \subset \mathcal{F} はどの2つも互いに素で, \sum_{n=1}^\infty B_n = \bigcup_{n=1}^\infty A_n, B_n\subset A_n である。ゆえに,
\begin{aligned}\mu\left(\bigcup_{n=1}^\infty A_n\right) &= \mu\left(\sum_{n=1}^\infty B_n\right) \\&= \sum_{n=1}^\infty \mu(B_n) \\ &\le \sum_{n=1}^\infty \mu(A_n).\end{aligned}
ただし,最後の不等式は性質2.を用いた。
証明終
4. μ(A_n) ↑ μ(A) について
4. \{A_n\}\subset\mathcal{F} かつ A_n\uparrow A とするとき, \mu(A_n)\uparrow \mu(A) である。
証明
性質2.より,\{ \mu(A_n)\} が広義単調増加であることはよい。
B_n =A_n\setminus A_{n-1} と定める。ただし, A_0=\emptyset と考える。このとき, \{B_n \}\subset \mathcal{F} は互いに素で
\begin{aligned}A_n &= \bigcup_{k=1}^n A_k = \sum_{k=1}^n B_k \\ A &= \bigcup_{k=1}^\infty A_k = \sum_{k=1}^\infty B_k \end{aligned}
が成り立つ。有限加法性(1.)と可算加法性より,
証明終
5. μ(A_n) ↓ μ(A) について
5. \{A_n\}\subset\mathcal{F} かつ \mu(A_n)<\infty かつ A_n \downarrow A とするとき, \mu(A_n)\downarrow \mu(A) である。
\mu(A_n)<\infty がないとこの定理は成立しません。実際,可測空間 (\mathbb{N}, 2^{\mathbb{N}}) 上の数え上げ測度 \# を考えると, \mathbb{N}_{\ge n} \downarrow \emptyset ですが, \lim_{n\to\infty} \#(\mathbb{N}_{\ge n} ) =\infty です。
証明
B_n = A_1\setminus A_n とすると,B_n \uparrow A_1 \setminus A である。性質4.より,
\!\! \begin{aligned}\mu(A_n) &= \mu(A_1)-\mu(B_n) \downarrow \mu(A_1)-\mu(A_1\setminus A)\\&= \mu(A_1)-\bigl(\mu(A_1)-\mu(A)\bigr)=\mu(A). \end{aligned}証明終
測度から積分へ
測度空間 (X, \mathcal{F},\mu) の上の可測関数 f\colon X\to\mathbb{R} に対しては,積分を考えることが可能です。ルベーグ積分 (Lebesgue integral) ですね。これについては,以下で解説しています。
測度における他の大事な概念
以下, (X,\mathcal{F}) を可測空間とします。
- 有限測度 (finite measure) …… \mu(X)<\infty となる測度のこと
- 確率測度 (probability measure) …… \mu(X)=1 となる有限測度のこと
- σ-有限測度 (σ-finite measure) …… \{A_n\} \subset \mathcal{F},\, A_n \uparrow X が存在して, \mu(A_n)<\infty とできる測度のこと
定義は覚えておきましょう。