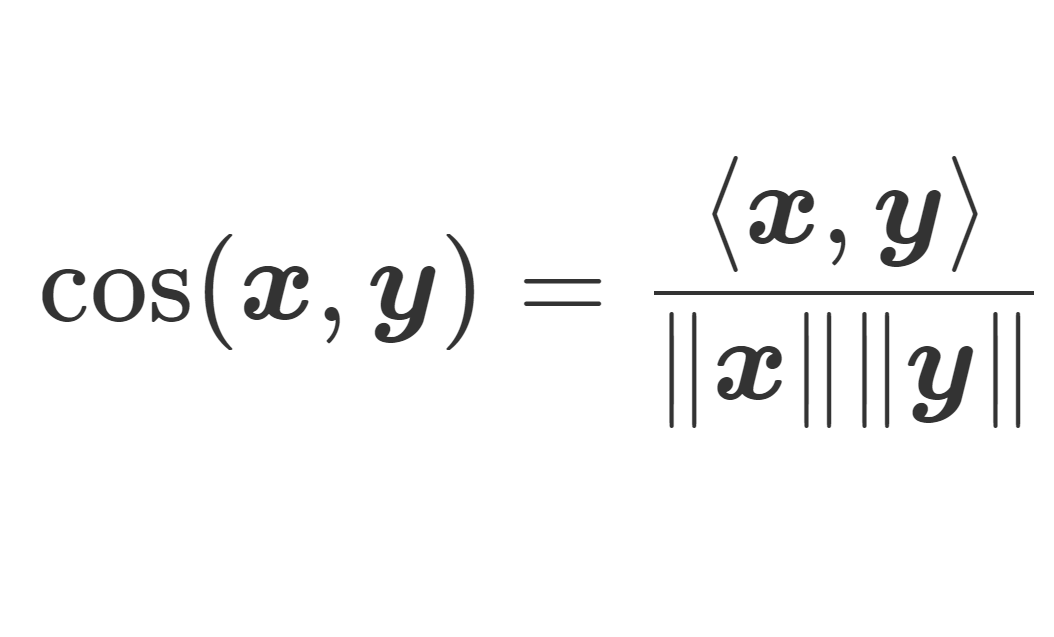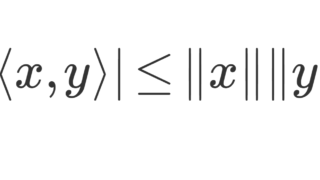コサイン類似度とは,ベクトルの向きの類似度を測る指標で,内積を用いて定義されます。コサイン類似度の定義と具体例を述べましょう。
コサイン類似度とは
定義(コサイン類似度)
ベクトル \boldsymbol{x}=\begin{pmatrix} x_1 \\ \vdots \\x_n \end{pmatrix},\boldsymbol{y} =\begin{pmatrix} y_1 \\ \vdots \\y_n \end{pmatrix}\in\mathbb{R}^n に対し,
\color{red}\large \begin{aligned}\cos(\boldsymbol{x}, \boldsymbol{y}) &= \frac{\langle\boldsymbol{x},\boldsymbol{y}\rangle}{\lVert\boldsymbol{x}\rVert \lVert\boldsymbol{y}\rVert }\\&=\frac{\sum_{k=1}^n x_ky_k}{\sqrt{ \sum_{k=1}^n x_k^2}\sqrt{ \sum_{k=1}^n y_k^2 }} \end{aligned}
をコサイン類似度 (cosine similarity) という。
ただし, \lVert\boldsymbol{x}\rVert =\sqrt{ \sum_{k=1}^n x_k^2} はノルム(ベクトルの大きさ), \langle\boldsymbol{x},\boldsymbol{y}\rangle = \sum_{k=1}^n x_ky_k はベクトルの内積を指す。
ベクトル同士の向きの「類似度」を測る指標です。
コサイン類似度はデータサイエンスの文脈でよく用いる言葉です。「コサイン」というのは,ベクトル \boldsymbol{x},\boldsymbol{y} のなす角を \theta としたときに,
\cos\theta= \frac{\langle\boldsymbol{x},\boldsymbol{y}\rangle}{\lVert\boldsymbol{x}\rVert \lVert\boldsymbol{y}\rVert }
となるからです。 n=2,3 次元のとき,ベクトルの内積を \langle\boldsymbol{x},\boldsymbol{y}\rangle = \lVert\boldsymbol{x}\rVert \lVert\boldsymbol{y}\rVert \cos\theta を定義したのを思い出しましょう。
なお,一般にコーシーシュワルツの不等式より
-1\le \frac{\langle\boldsymbol{x},\boldsymbol{y}\rangle}{\lVert\boldsymbol{x}\rVert \lVert\boldsymbol{y}\rVert } \le 1
が成り立ちます。 1 に近い方が類似度が大きく, -1 に近い方がベクトルの向きは逆向きに近くなります。コサイン類似度はベクトルの向きのみが関係し,大きさは影響しません。以下の具体例でも確認してみましょう。
なお, x_1, \dots, x_n や y_1, \dots, y_n の平均が 0 のときは,コサイン類似度は相関係数の定義に一致します。
コサイン類似度の具体例
n=2 次元の場合の具体例を図示しておきましょう。このとき,
\begin{aligned}\cos(\boldsymbol{x}, \boldsymbol{y}) = \frac{\langle\boldsymbol{x},\boldsymbol{y}\rangle}{\lVert\boldsymbol{x}\rVert \lVert\boldsymbol{y}\rVert }=\frac{x_1y_1+x_2y_2}{\sqrt{x_1^2+x_2^2}\sqrt{ y_1^2+y_2^2 }} \end{aligned}
であることに注意します。
| 図 | \cos(\boldsymbol{x},\boldsymbol{y}) | 状態 |
|---|---|---|
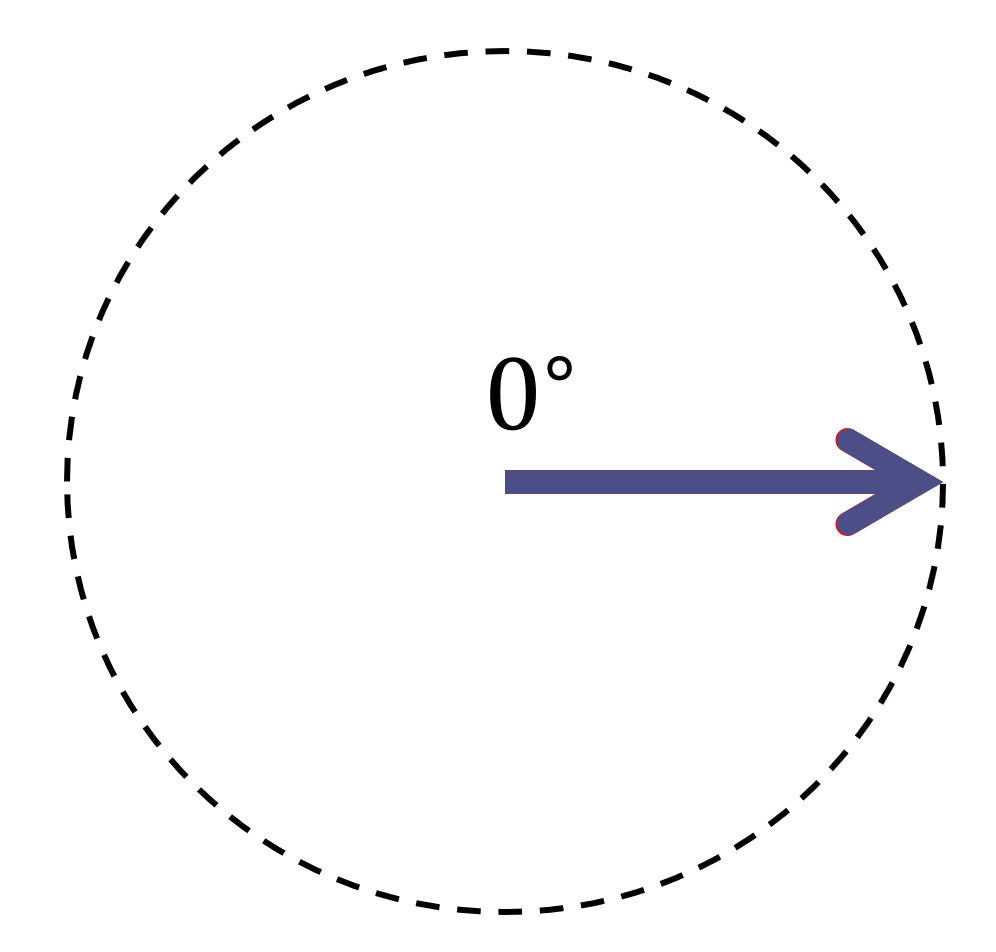 | \Huge 1 | 似ている |
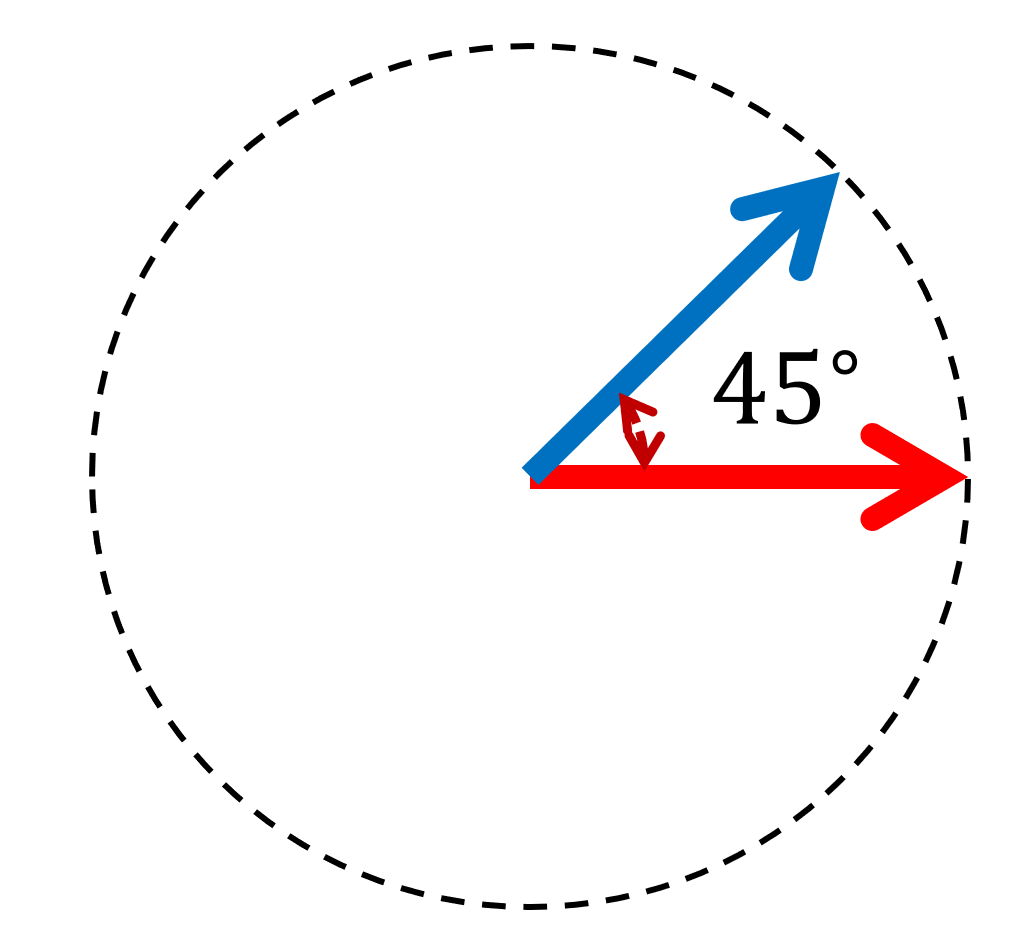 | \Huge \frac{1}{\sqrt{2}} | |
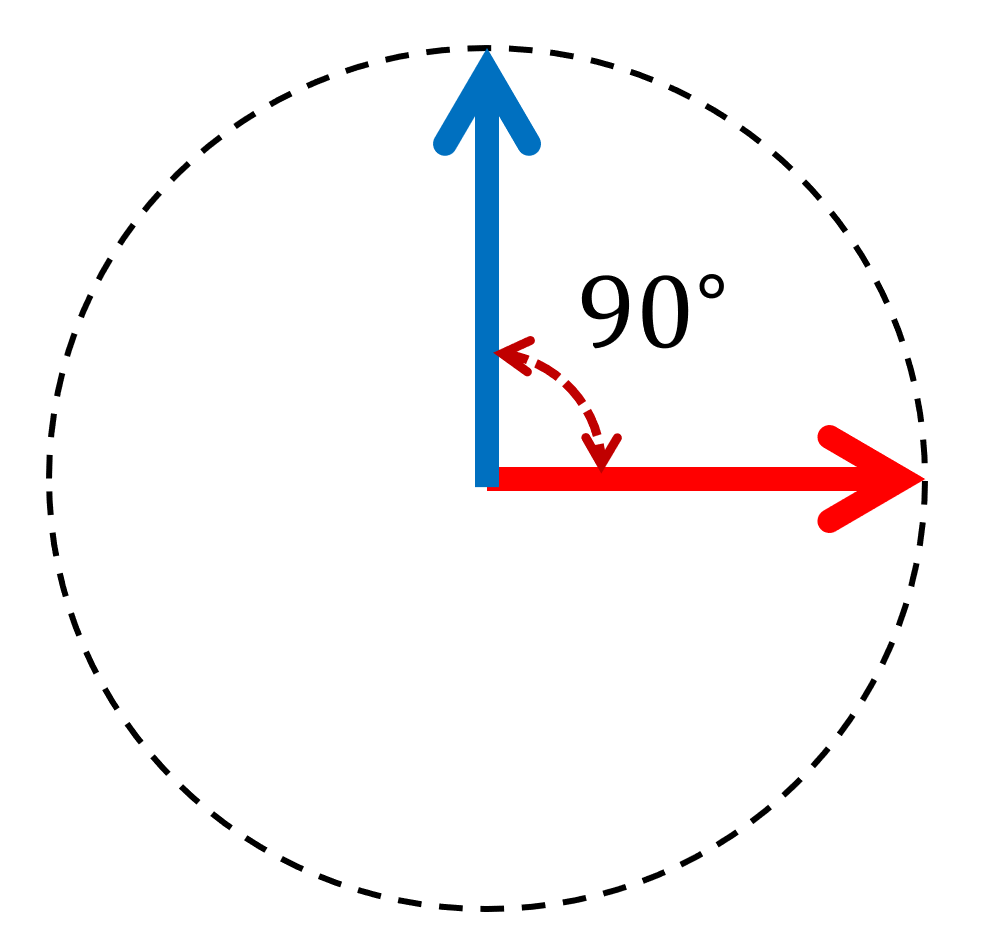 | \Huge 0 | |
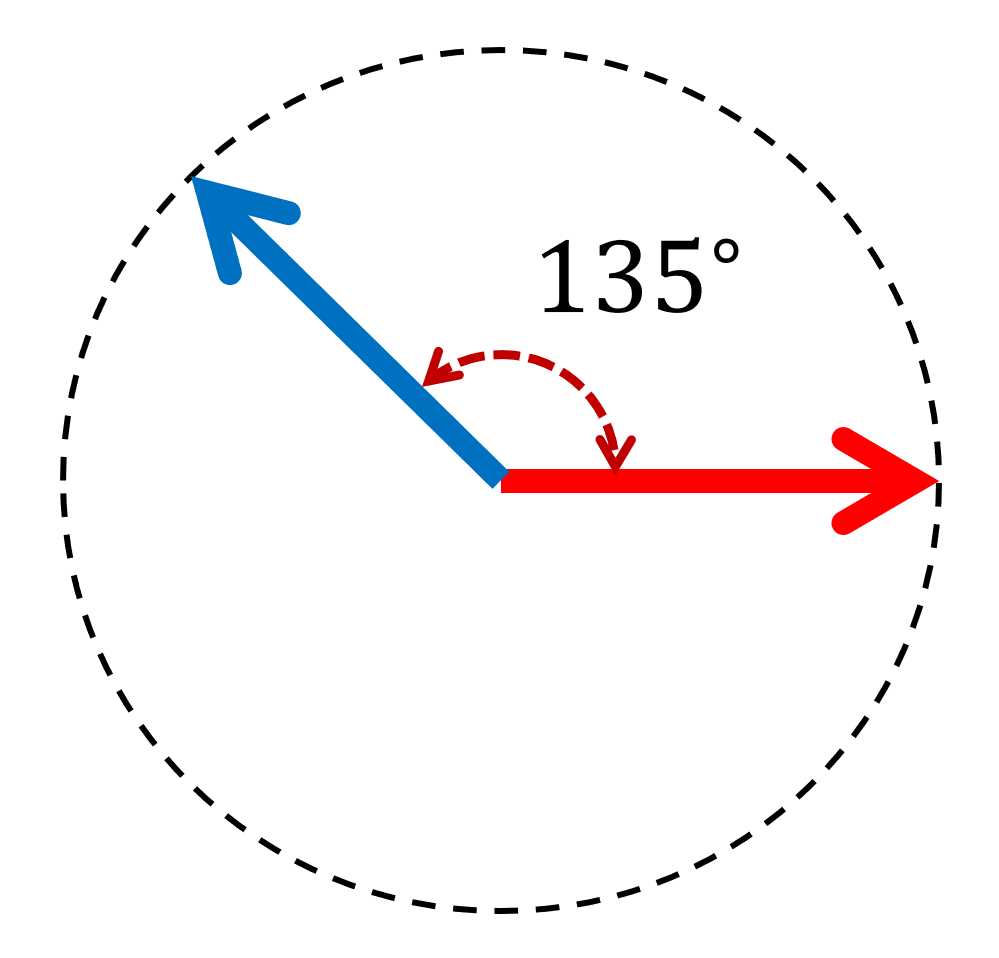 | \Huge -\frac{1}{\sqrt{2}} | |
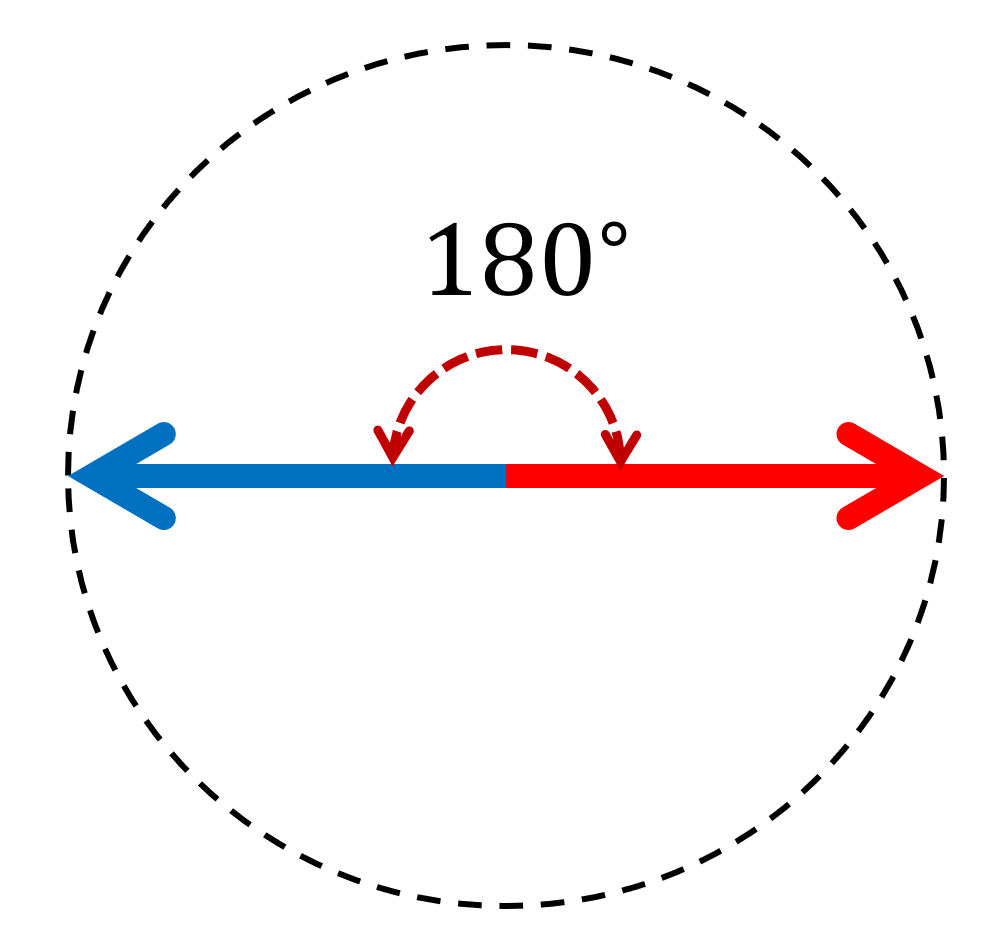 | \Huge -1 | 逆向き |
コサイン類似度は,データサイエンスにおいて,自然言語処理などで用いられます。ベクトルの内積を「類似度」とみる見方はうまいですね。
なお,次元 n が十分大きいときには,コサイン類似度は 0 付近の値を取りやすくなります。 n=2 のときは \boldsymbol{x} =(1,0) と垂直になるのは \boldsymbol{y}=(0, *) の形のみですが,n が大きいと \boldsymbol{x}=(1,0,\dots, 0) と垂直になるのは \boldsymbol{y} = (0, *,\dots, *) となり,垂直になりやすくなるからです。 「次元の呪い」ですね。