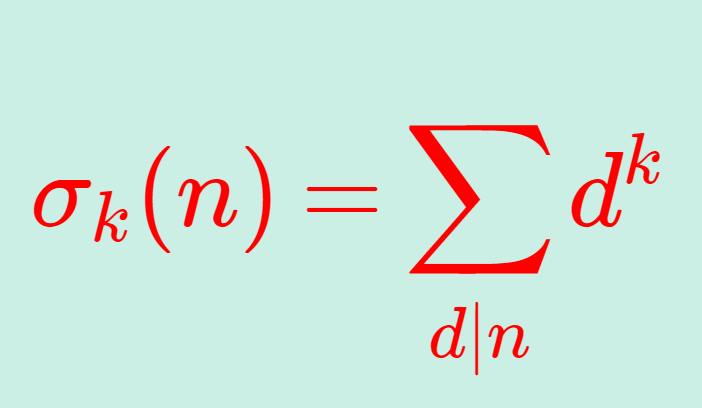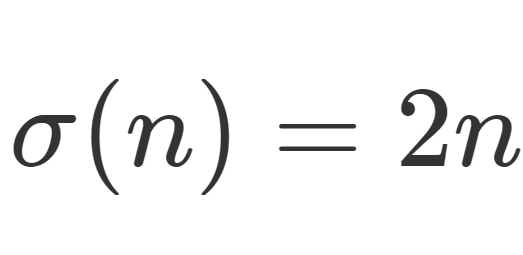約数関数とは,ある数に対し,その数の正の約数の累乗の和を計算する関数です。約数関数について,その定義と基本的な性質とその証明を行いましょう。
約数関数とは
定義(約数関数)
n\in\mathbb{Z}_{\ge 1},\; k\in\mathbb{Z} に対し,
\Large\color{red} \sigma_k(n) =\sum_{d\mid n} d^k
を約数関数 (divisor function) という。 \sum_{d\mid n} とは, n の正の約数全体で和を取ることを表す。
特に \color{red}\sigma(n)=\sigma_1(n) は正の約数の総和を表し, \color{red}d(n)=\sigma_0(n) は正の約数の個数を表す。
たとえば, 15 の正の約数は 1,3,5,15 ですから, \sigma_k(15) = 1^k+3^k+5^k+15^k です。特に,約数の総和は \sigma(15)=1^1+3^1+5^1+15^1 = 24 で,約数の個数は d(15) = 1^0+3^0+5^0+15^0 = 4 となります。
約数関数の性質とその証明
約数の性質で,最も基本的で重要なものを挙げましょう。
定理(約数関数の性質)
n = \prod_{i=1}^r p_i^{a_i} = p_1^{a_1} \dots p_r^{a_r} を整数 n\in\mathbb{Z}_{\ge 2} の素因数分解とする。このとき,
\color{red} \begin{aligned} \sigma_k(n) &= \prod_{i=1}^r (1+p_i^{k}+p_i^{2k}+\dots +p_i^{a_ik}) \\ &= \prod_{i=1}^r \frac{p_i^{(1+a_i)k}-1}{p_i^k - 1} \end{aligned}
が成り立つ。特に,
である。また, m,n \in\mathbb{Z}_{\ge 2} が互いに素ならば \color{red}\sigma_k(mn) = \sigma_k(m)\sigma_k(n). すなわち \sigma_k は乗法的関数である。
素因数分解さえできれば,約数関数は計算可能ということですね。
証明は簡単です。
証明
\begin{aligned} \sigma_k(n) &= \sum_{d\mid n} d^k \\ &= \sum_{0\le b_1 \le a_1, \dots, 0\le b_r\le a_r} p_1^{b_1}\dots p_r^{b_r}\\ &= \sum_{b_1=0}^{a_1} \dots \sum_{b_r=0}^{a_r} p_1^{b_1}\dots p_r^{b_r} \\ &= \sum_{b_1=0}^{a_1} p_1^{b_1} \dots \sum_{b_r=0}^{a_r} p_r^{b_r} \\ &= \prod_{i=1}^r \sum_{b_i=0}^{a_i} p_i^{b_i} \end{aligned}
より,示せた。また,m,n が互いに素ならば, m=\prod_{i=1}^{r} p_i^{a_i} ,\; n=\prod_{i=1}^{r'} p_{r+i}^{a_{r+i}} を素因数分解としたときに同じ素数は現れず,mn = \prod_{i=1}^{r+r'} p_i^{a_i} は素因数分解になる。ゆえに,
なので,\sigma_k は乗法的である。
証明終