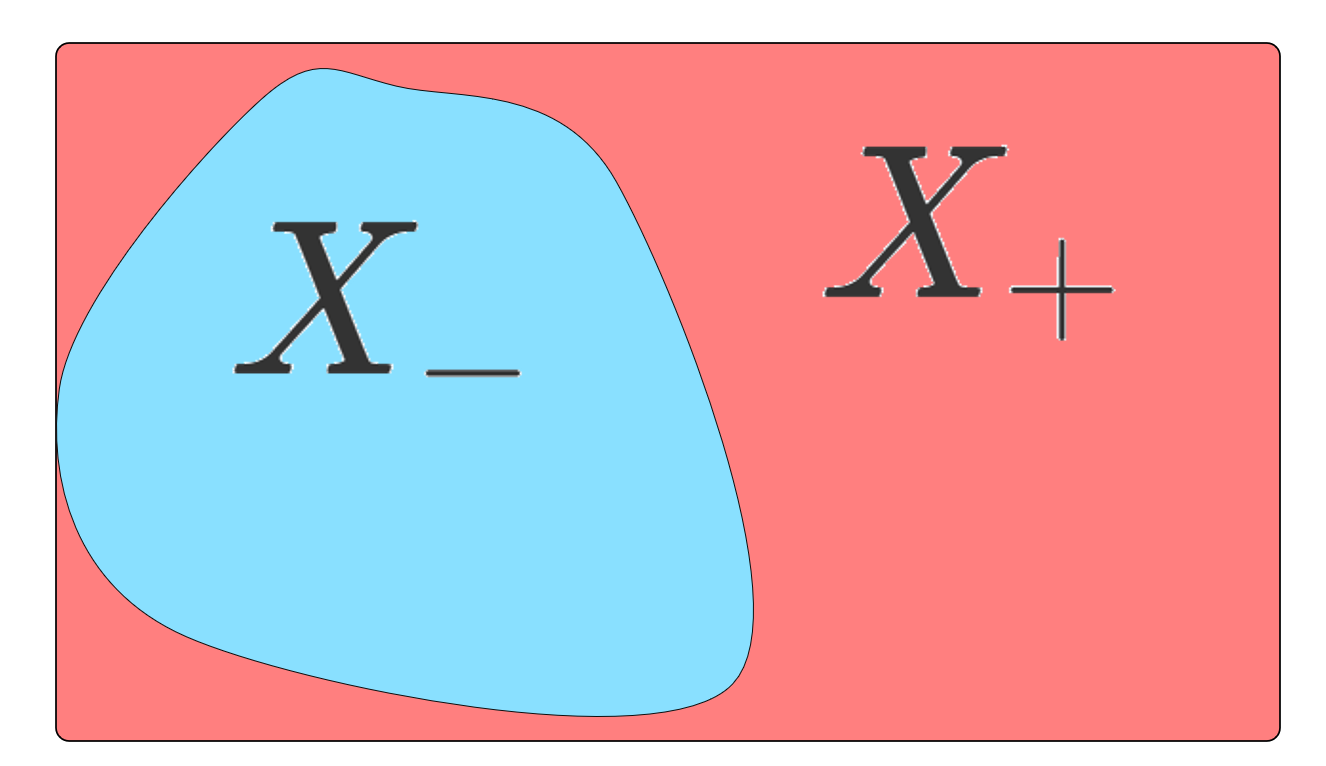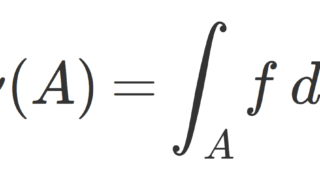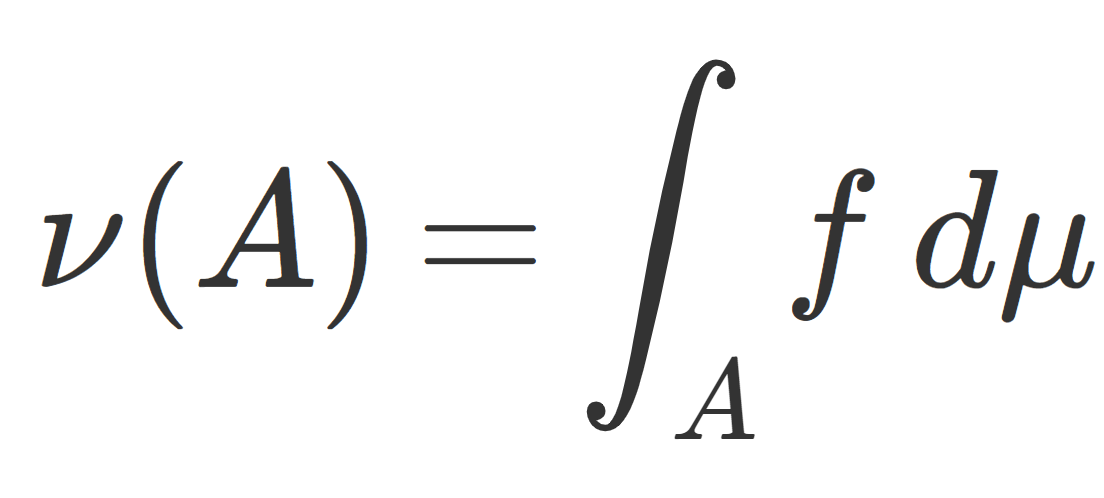符号付き測度・複素測度とは,それぞれ \mu\colon \mathcal{F}\to \R や \mu\colon \mathcal{F}\to \mathbb{C} のように,負の値や複素数値を許すような測度のことです。
符号付き測度・複素測度について,その定義と例,分解定理を解説しましょう。
符号付き測度・複素測度の定義と例
符号付き測度・複素測度の定義
まず,測度の定義を復習しておきましょう。以下について詳しくは測度の定義と具体例4つ・性質5つを証明付きで徹底解説で解説しています。
\mu \colon \mathcal{F}\to \boldsymbol{\textcolor{red}{[0,\infty]}} の赤字の部分を変えたものが符号付き測度・複素測度です。
定義(符号付き測度・複素測度)
上の測度の定義において,
- \mu\colon \mathcal{F}\to \boldsymbol{\textcolor{red}{\R}} に変えたものを符号付き測度 (signed measure),
- \mu\colon \mathcal{F}\to \boldsymbol{\textcolor{red}{\mathbb{C}}} に変えたものを複素測度 (complex measure)
という。
符号付き測度・複素測度においては,等式 \mu\left(\bigcup_{n=1}^\infty A_n\right) = \sum_{n=1}^\infty \mu (A_n) が well-defined かという問題があります。どの二つも互いに素な任意の集合 \{A_n\}\subset \mathcal{F} について,無限和 \sum_{n=1}^\infty \mu (A_n) は絶対収束してなければなりません。
もし絶対収束ではなく,条件収束だったとすると,条件収束級数は和の順序交換により任意の値に収束できることの証明により,集合列 \{A_n\} の並び替えにより,和が変わってしまいますから,一つの値 \mu\left(\bigcup_{n=1}^\infty A_n\right) に収束することはあり得なくなってしまいます。後で紹介するハーンの分解定理から,このことが成り立つためには,
-\infty<\inf_{A\in\mathcal{F}}\mu(A)\le\sup_{A\in\mathcal{F}}\mu(A)<\infty
でなくてはならないことが分かります。
なお,符号付き測度については, \mu\colon \mathcal{F}\to [-\infty, \infty] のように, \pm\infty 値を許すことも多いです。ただし, \infty-\infty は定義できないため, \mu(A)=\infty,\, \mu(B)=-\infty となる A,B\in\mathcal{F} は同時に存在してはなりません。すなわち, -\infty か \infty の少なくとも一方は \mu の値域ではありません。
符号付き測度・複素測度の例
例1.
X= \{-10,-9,-8,\dots, -1,0,1,\dots 10\} とする。可測空間 (X, 2^X) について,\mu(A) を, A のうち正の数の個数から負の数の個数を引いたものと定義すると,\mu は符号付き測度である。
数え上げ測度の符号付き測度バージョンといったところでしょうか。
例2.
(X,\mathcal{F}) を可測空間とし,\nu_1 ,\nu_2,\nu_3,\nu_4 をその上の有限測度とする。このとき,
\mu=\nu_1-\nu_2
は符号付き測度である。また,
は複素測度である。
逆に,全ての符号付き測度や複素測度は上の形に分解することができます。「ジョルダンの分解定理」として,あとで紹介します。
例3.
(X,\mathcal{F},\nu) を測度空間, f\colon X\to \R (\mathbb{C}) を可積分関数とする。このとき,A\in\mathcal{F} に対し,
\mu(A)=\int_A f(x)\, d\nu(x)
で定義される \mu\colon \mathcal{F}\to \R(\mathbb{C}) は符号付き測度(複素測度)である。
逆に,\mu,\nu がσ有限測度であり,かつ \mu が \nu に関して絶対連続ならば,上のような等式を成り立たせる f が存在することが知られています。これをラドンニコディムの定理 (Radon–Nikodym theorem) といいます。以下で紹介しています。
ハーンの分解定理
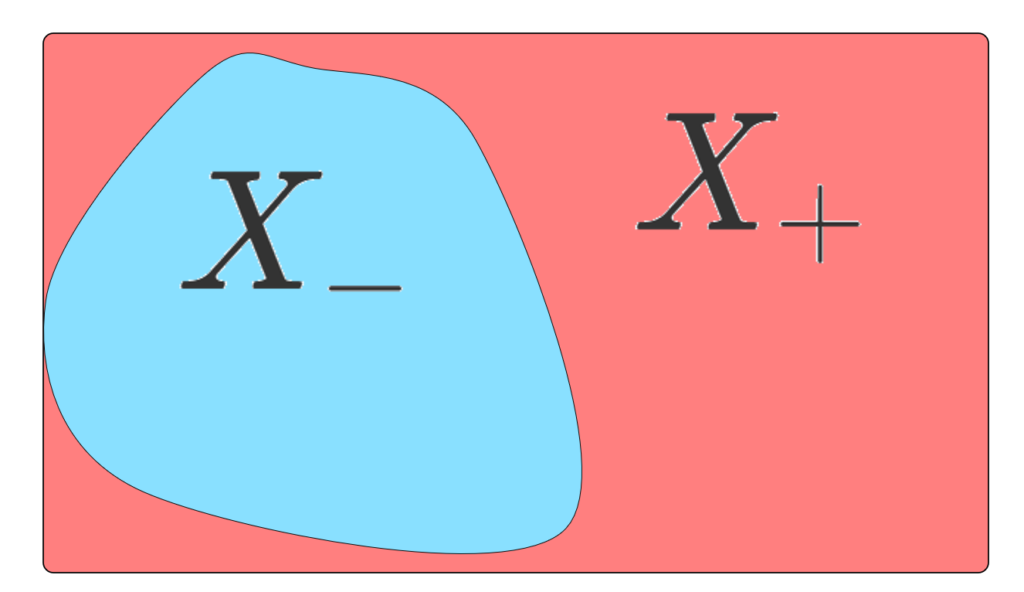
ハーンの分解定理 (Hahn decomposition theorem)
(X,\mathcal{F}) を可測空間とし, \mu\colon X\to \R を符号付き測度とする。このとき,以下をみたす X_+,X_-\in \mathcal{F} が存在する。
- X_+\cap X_- =\emptyset
- X_+\cup X_- =X
- \mu(A\cap X_+)\ge 0,\; \mu(A\cap X_-)\le 0,\quad A\in\mathcal{F}
また,このような X_+,X_- は零集合の差を除いて一意的である。
ここで, N\in\mathcal{F} が零集合 (null set) とは,任意の A\in \mathcal{F} に対し, \mu(N\cap A)=0 が成り立つこととします。単に \mu (N)=0 としてしまうと,符号付き測度の場合はまずいです。集合 A,A' が零集合の差を除いて一意的とは,対称差 A\bigtriangleup A'=(A\setminus A')\cup (A'\setminus A) について,\mu(A\bigtriangleup A')=0 が成り立つことを指します。
以下で, P\in\mathcal{F} が正集合 (positive set) であるとは,任意の可測集合 E\subset P に対し, \mu(E)\ge 0 が成り立つことと定義します。このとき, \mu|_P は符号付きではない,ただの測度です。逆に, N\in\mathcal{F} が負集合 (negative set) であるとは,任意の可測集合 E\subset N に対し, \mu(E)\le 0 が成り立つことと定義します。
証明
まず,任意の A\in \mathcal{F} に対し, \mu(P)\ge \mu(A) をみたすある正集合 P\subset A が存在することを示そう。 \varepsilon>0 とすると,ある A_\varepsilon \subset A が存在して, \mu(A_\varepsilon)\ge \mu(A) かつ, B\subset A_\varepsilon\implies \mu(B)>-\varepsilon とできる。もしそうでなかったとすると, B_1\subset A で \mu(B_1)\le -\varepsilon をみたすものが存在し,また B_2\subset A\setminus B_1 で \mu(B_2)\le -\varepsilon をみたすものが存在し,帰納的に B_n \subset A\setminus\bigcup_{k=1}^{n-1} B_k で \mu(B_n)\le -\varepsilon をみたすものが存在する。 \{B_n\} は互いに素な集合で,\mu(\bigcup B_n )=\sum\mu(B_n)=-\infty となってしまい, \mu が実数値を取ることに矛盾するからである。
ここで,\{ A_{1/m}\}_m は減少列となるように取り直すことができ, P=\bigcap_{m} A_{1/m} とすると, P は正集合となる。また,\{ A_{1/m}\}_m は減少列より, \lim_m \mu(A_{1/m}) =\mu(P) が成り立つことが,符号付き測度の定義2.より導ける。よって \mu(P)\ge \mu(A) も成り立つ。
次に,定理を示そう。 \alpha_+ =\sup_{A\in\mathcal{F}} \mu(A) \in [0,\infty] と定める。supの定義より,ある \{A_n\}\subset \mathcal{F} が存在して, \mu(A_n)\ge 0 かつ \lim_{n\to\infty} \mu(A_n)=\alpha_+ とできる。上に示したことより, A_n は正集合としてよい。
X_+=\bigcup_{n=1}^\infty A_n とすると, X_+\in \mathcal{F} であり,明らかに X_+ も正集合である。supの定義より, \mu(X_+)=\alpha_+ である。 \mu\colon \mathcal{F}\to \R より特に 0<\alpha_+<\infty となる。さらに, X_-=X\setminus X_+ とする。このとき, X_+, X_- は明らかに定理の項目1,2.をみたす。さらに X_+ は正集合より,3.の一つ目の式をみたす。 X_- が3.をみたすことを示そう。
\mu(A\cap X_-)>0 と仮定すると, \mu(X_+\cup (A\cap X_-)) = \mu(X_+)+\mu(A\cap X_-) >\mu(X_+) となって,supの定義に矛盾している。よって,示せた。
また,明らかに X_+ は零集合の差を除いて一意的でなければならない。一意でなかったとすると,2つある X_+, X_+' に対し, \mu(X_+\cup X_+')>\alpha_+ となってしまうからである。したがって, X_- も零集合の差を除いて一意的である。
証明終
\mu\colon \mathcal{F}\to [-\infty, \infty) でも証明は上と同様です。最初の議論で \mu\ne -\infty を使っていますが,これは後半では \mu(A_n)\ge 0 上に限定して使っているので問題ありません。 \mu\colon \mathcal{F}\to (-\infty, \infty] の場合は -\mu に対して,上の証明をすればよいです。
ジョルダンの分解定理
ジョルダンの分解定理は,符号付き測度や複素測度を,測度に分解する定理です。
ジョルダンの分解定理 (Jordan decomposition theorem)
(X,\mathcal{F}) を可測空間とする。
\mu\colon X\to \R を符号付き測度とすると,ある特異な測度 \mu_+, \mu_-\colon \mathcal{F}\to [0,\infty) が一意的に存在して,
\large \color{red}\mu= \mu_+ - \mu_-
とできる。ただし \mu_+ と \mu_- が特異とは,ある X_+\in\mathcal{F} が存在して, \mu_+(X_+^c)=\mu_-(X_+)=0 とできることを指す(→測度の絶対連続性・同値性・特異性とルベーグ分解)。
\mu\colon X\to \mathbb{C} を複素測度とすると,ある測度 \mu_{R+}, \mu_{R-}, \mu_{I+}, \mu_{I-}\colon \mathcal{F}\to [0,\infty) が一意的に存在して,
\color{red}\mu=\mu_{R+}-\mu_{R-}+i\mu_{I+}-i\mu_{I-}
で,\mu_{R+} と \mu_{R-} は特異,\mu_{I+} と \mu_{I-} は特異とできる。
なお,符号付き測度は \mu\colon X\to [-\infty,\infty] としても \mu_+, \mu_-\colon \mathcal{F}\to [0,\infty] が一意的に存在して同じです。証明も同じです。
証明
前半について ハーンの分解定理より,
\mu_+ =\mu(\cdot \cap X_+), \quad \mu_-=\mu(\cdot \cap X_-)
と定めればよい。
後半について
\operatorname{Re}\mu, \operatorname{Im} \mu は符号付き測度であるから,これに前半を適用すればよい。
証明終
符号付き測度 \mu=\mu_+-\mu_- において,測度 |\mu| =\mu_+ + \mu_- を \mu の変分 (変動; variation) といい,値 |\mu|(X) を全変動 (total variation) ということがあります。全変動は A\in\mathcal{F} に対し,
|\mu|(A)=\sup_{B\in\mathcal{F}}\bigl(|\mu(B)|+|\mu(A\setminus B)|\bigr)
とも定義できます。これとラドンニコディムの定理を認めると,ラドンニコディム微分 d\mu/d|\mu| について, X_+=\{d\mu/d|\mu|\ge 0\},\, X_-=\{d\mu/d|\mu|< 0\} と定めることで,ハーンの分解定理を証明することができます。