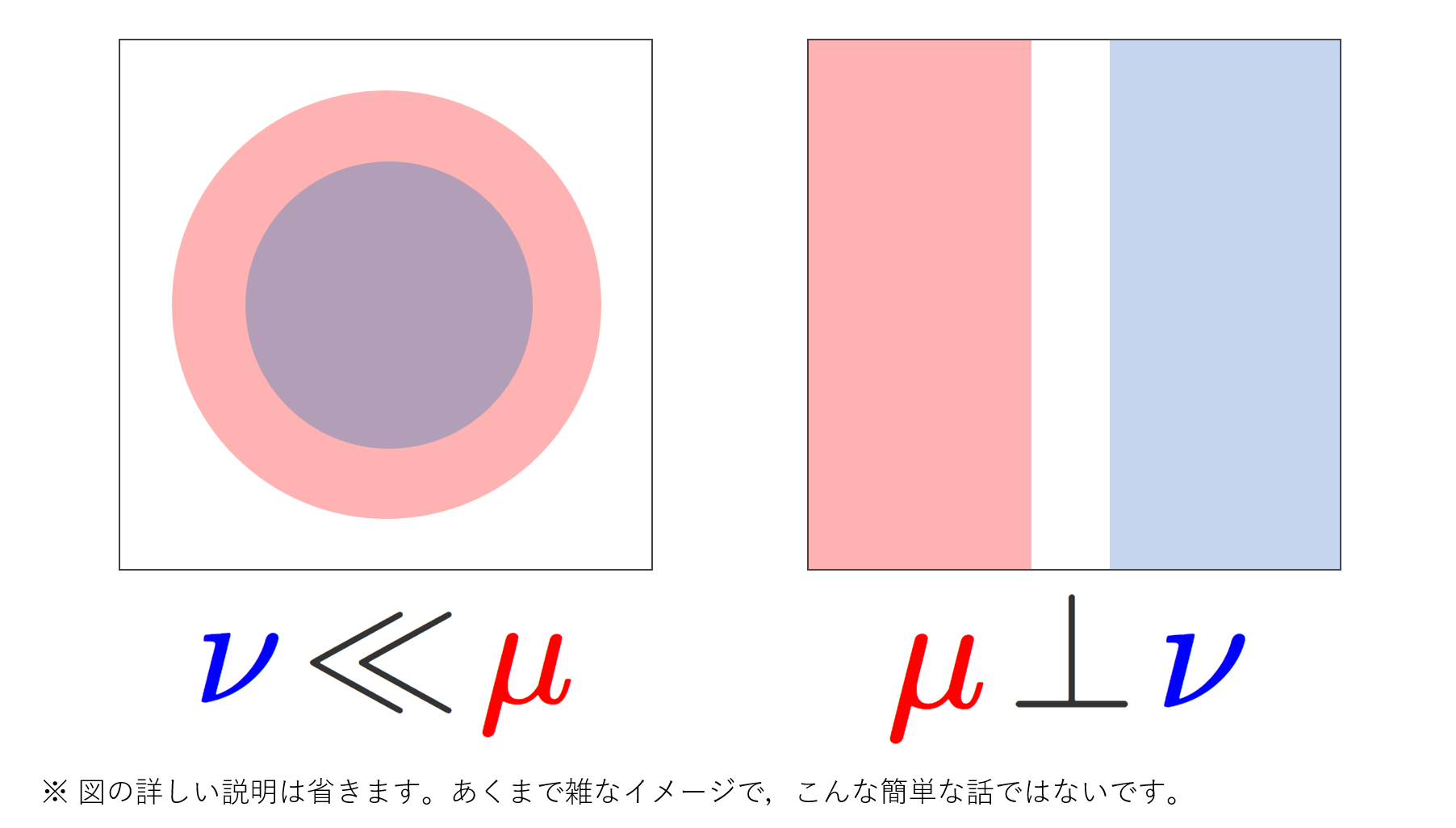
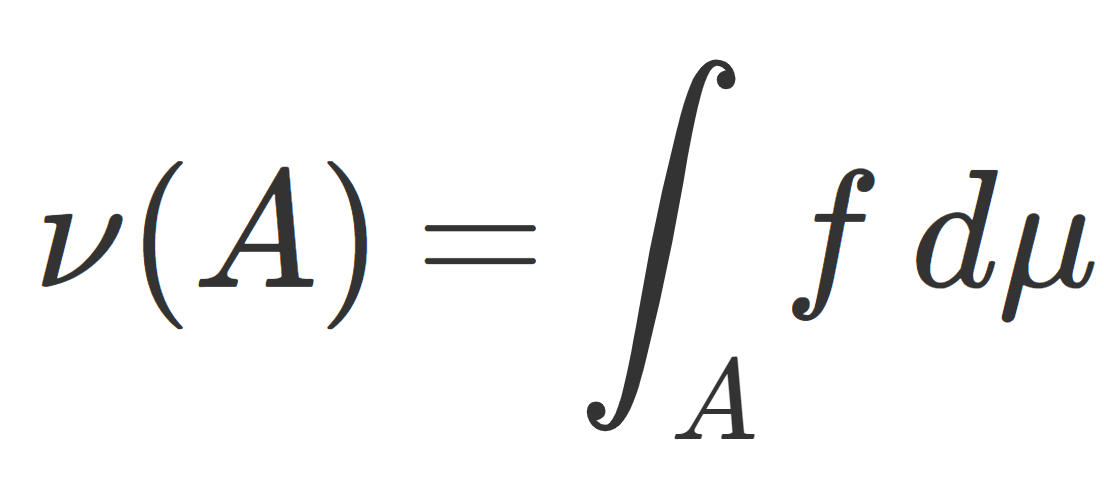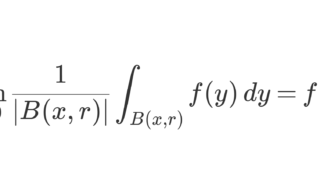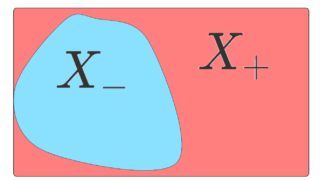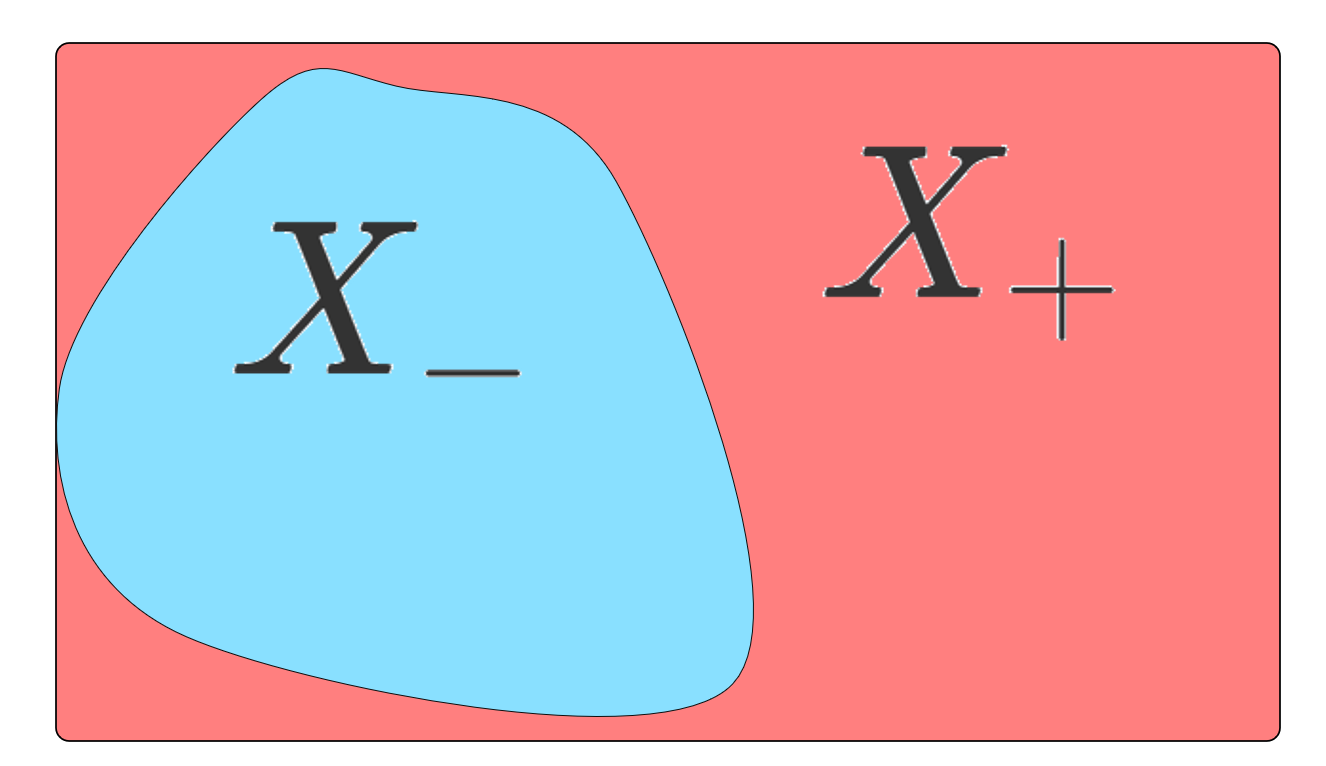ラドンニコディムの定理とその2通りの証明

ラドンニコディムの定理と呼ばれる，測度論における「微分」を扱う定理を紹介しましょう。

これは確率論における条件付き期待値にも使われる概念であり，とても重要です。

ラドンニコディムの定理
ラドンニコディムの定理の2通りの証明
1. 1. 測度論を用いた証明
2. 2. 関数解析を用いた証明
符号付き測度・複素測度におけるラドンニコディムの定理
測度の微分はラドンニコディム微分
関連する記事

ラドンニコディムの定理

ラドンニコディムの定理 (Radon–Nikodym theorem)

$(X,\mathcal{F})$ を可測空間， $\mu,\nu$ をその上のσ有限な測度とする。さらに $\nu$ が $\mu$ に関して絶対連続( $\color{red}\nu \ll \mu$ )とする。このとき， $\mu$ に関して局所可積分な非負関数 $f\in L^1_{\mathrm{loc},+}(\mu)$ が( $\mu$ –a.e.の意味で)一意的に存在して，

\color{red}\nu(A)=\int_A f \, d\mu,\quad A\in \mathcal{F}

とかける。このときの $f$ を $\color{red} \dfrac{d\nu}{d\mu}$ とかき，ラドンニコディム密度 (Radon-Nikodym density) またはラドンニコディム微分 (Radon-Nikodym derivative) という。

$\nu$ が $\mu$ に関して絶対連続 (absolutely continuous) とは， $\mu(A)=0\implies \nu(A)=0$ が成り立つことです(→測度の絶対連続性・同値性・特異性とルベーグ分解)。

$f$ が局所可積分 (locally integrable) とは， $A\in\mathcal{F}$ が $\mu(A)<\infty$ をみたすならば $\int_A |f|\ d\mu<\infty$ をみたすということです。

なお， $\mu,\nu$ がσ有限な測度というのは，本定理の本質です。実際， $(\R, \mathcal{B}(\R))$ 上の数え上げ測度を $\#$ ，ルベーグ測度を $\mu$ とすると，数え上げ測度はσ有限ではなく，一方 $\mu \ll \#$ は成立します。このとき，もし $f\in L^1_{\mathrm{loc},+}(\#)$ で

\mu(A)= \int_A f \, d\#

をみたすものが存在したとすると， $A=\{a\}$ とすることで， $f(a)=0$ となりますが，これだと $\mu$ が零測度になってしまい矛盾してしまいます。

ラドンニコディムの定理の2通りの証明

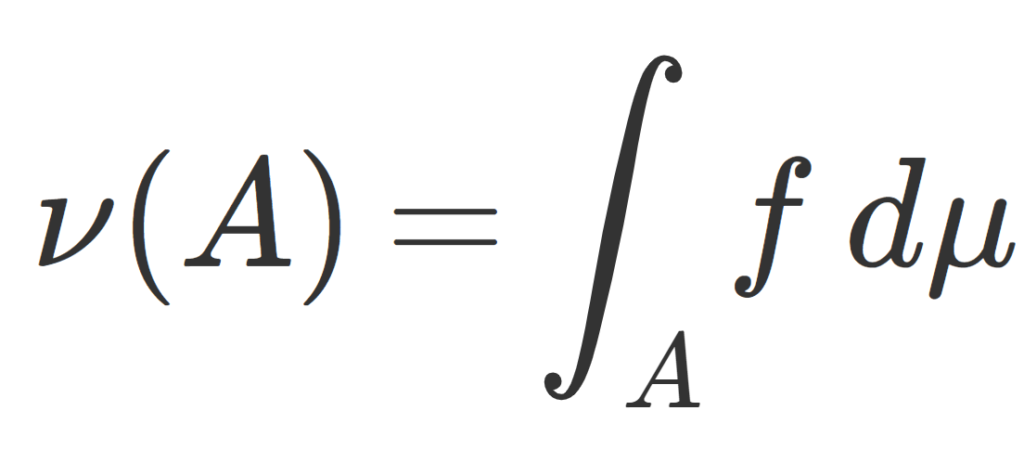
ラドンニコディムの定理の証明を，

測度論を用いた証明
関数解析を用いた証明

の2通り紹介しましょう。

1. 測度論を用いた証明

測度論を用いた証明

一意性は【数学科向け】ルベーグ積分の定義を段階を踏んで解説するの定理A.5より明らかなので，存在について示す。

まず， $\mu,\nu$ を有限測度とする。

F=\left\{ g \in L_+^1(\mu) \middle| \forall A\in \mathcal{F}, \int_A g\, d\mu\le \nu(A) \right\}

とする。 $0\in F$ より， $F\ne \emptyset$ である。ここで， $g_1, g_2\in F$ とすると， $\max\{ g_1, g_2\}\in F$ である。実際，任意の $A\in\mathcal{F}$ に対し，

\begin{aligned} &\int_A \max\{ g_1, g_2\}\, d\mu\\ &= \int_{A\cap \{ g_1\ge g_2\}} g_1\, d\mu +\int_{A\cap \{ g_1< g_2\}} g_2\, d\mu \\ &\le \nu(A\cap \{ g_1\ge g_2\})+\nu(A\cap \{ g_1< g_2\}) \\ &= \nu(A) \end{aligned}

であるからである。ここで， $\{g_n\} \subset F$ を

\lim_{n\to\infty} \int_X g_n\, d\mu=\sup_{g\in F} \int_X g\, d\mu

となるように定める。 $f_n =\max\{ g_1, g_2, \dots, g_n\}$ とすると， $\{ f_n\}\subset F$ は増大列であり，

\lim_{n\to\infty} \int_X f_n\, d\mu=\sup_{g\in F} \int_X g\, d\mu

である。 $f=\lim_{n\to\infty } f_n$ と定めると，単調収束定理より，

\int_X f\, d\mu=\sup_{g\in F} \int_X g\, d\mu

であり，さらに同じ定理から $f\in F$ もわかる。ここで， $f$ が求めるものであることを背理法で示す。ある $A\in \mathcal{F}$ で， $\int_A f\, d\mu < \nu(A)$ を仮定する。このとき， $\int_X f\, d\mu < \nu(X)$ である。そこで，

\nu_0(A)=\nu(A)-\int_A f\, d\mu,\quad A\in\mathcal{F}

として測度 $\nu_0$ を定義する。 $\nu_0(X)>0$ であるから，ある $\varepsilon >0$ が存在して， $\nu_0(X)>\varepsilon \mu(X)$ とできる。符号付き測度 $\nu_0-\varepsilon \mu$ におけるハーンの分解を $X=X_+\cup X_-$ とする。 $(\nu_0-\varepsilon\mu)(X)>0$ より， $(\nu_0-\varepsilon\mu)(X_+)>0$ である。このとき， $A\in\mathcal{F}$ に対し， $\nu_0(A\cap X_+)\ge \varepsilon \mu(A\cap X_+)$ であり，

\begin{aligned} \int_A(f+\varepsilon 1_{X_+})\, d\mu &= \int_A f\, d\mu +\varepsilon\mu(A\cap X_+) \\ &\le \int_A f\, d\mu +\nu_0(A\cap X_+) \\ &\le \int_A f\, d\mu +\nu_0(A) \\ &= \nu(A) \end{aligned}

なので， $f+\varepsilon 1_{X_+}\in F$ である。 $\mu(X_+)=0$ とすると，絶対連続性より $\nu(X_+)=0$ となって， $(\nu_0-\varepsilon\mu)(X_+)>0$ に矛盾する。したがって， $\mu(X_+)>0$ であり，

\begin{aligned} \int_X (f+\varepsilon 1_{X_+})\, d\mu &> \int_X f\, d\mu \\ &=\sup_{g\in F} \int_X g\, d\mu \end{aligned}

であるが，これは矛盾している。よってやはり $f$ が求めるものである。

$\mu, \nu$ がσ有限のとき

全体空間 $X$ をどの2つも互いに素な $\{X_n\}$ で， $\mu(X_n),\nu(X_n)<\infty$ となるものに分割して同様のことを考えればよい。

証明終

2. 関数解析を用いた証明

実ヒルベルト空間論を用いた証明も紹介しておきましょう。関数解析の知識が必要です。

関数解析を用いた証明

一意性は【数学科向け】ルベーグ積分の定義を段階を踏んで解説するの定理A.5より明らかなので，存在について示す。

まず， $\mu,\nu$ を有限測度とする。

$g\colon X\to \R$ を $g\in L^2(\mu+\nu)$ とする。コーシーシュワルツの不等式より，

\begin{aligned}&\int|g| \,d(\mu+\nu) \\ &\le \left(\int |g|^2\,d(\mu+\nu) \right)^{1/2} \left(\int 1^2\,d(\mu+\nu) \right)^{1/2} \\ &= \|g\|_{L^2(\mu+\nu)}\sqrt{ (\mu+\nu)(X)}. \end{aligned}

ゆえに $L^2(\mu+\nu)\subset L^1(\mu+\nu)\subset L^1(\mu)$ である。したがって，

\varphi(g)=\int g\, d\mu

によって，線形汎関数 $\varphi\colon L^2(\mu+\nu)\to\R$ が定まり，有界である。リースの表現定理より，ある $f_1\in L^2_+(\mu+\nu)$ が存在して，

\int g\, d\mu = \int gf_1\, d(\mu+\nu),\quad g\in L^2(\mu+\nu)

とできる。同様にある $f_2\in L^2_+(\mu+\nu)$ が存在して，

\int g\, d\nu = \int g f_2\, d(\mu+\nu),\quad g\in L^2(\mu+\nu)

とできる。辺々足し算すると， $\int g\, d(\mu+\nu)=\int g (f_1+f_2)\, d(\mu+\nu)$ となるため， $f_1+f_2=1,\, (\mu+\nu)\text{-a.e.}$ がわかる。ここで，

\begin{aligned}\mu(f_1=0)&=\int 1_{\{f_1=0\}}\, d\mu \\&= \int 1_{\{f_1=0\}}f_1\, d(\mu+\nu)=0 \end{aligned}

であり，さらに $\nu\ll\mu$ より $(\mu+\nu)(f_1=0)=0$ である。したがって， $(\mu+\nu)\text{-a.e.}$ の意味で

f=\frac{f_2}{f_1}

と定義できて，任意の $g\in L^2(\mu+\nu)$ で

\begin{aligned} \int gf\, d\mu &= \int gff_1\, d(\mu+\nu) \\ &= \int gf_2\, d(\mu+\nu) \\ &= \int g\, d\nu \end{aligned}

となる。 $g=1_{A}$ とすることで，結論を得る。

$\mu, \nu$ がσ有限のとき

全体空間 $X$ をどの2つも互いに素な $\{X_n\}$ で， $\mu(X_n),\nu(X_n)<\infty$ となるものに分割して同様のことを考えればよい。

証明終

符号付き測度・複素測度におけるラドンニコディムの定理

ラドンニコディムの定理は， $\nu$ を符号付き測度や複素測度に拡張することが可能です。

ラドンニコディムの定理2 (Radon–Nikodym theorem)

$(X,\mathcal{F})$ を可測空間， $\mu$ をその上のσ有限な測度， $\nu$ をσ有限な符号付き測度(複素測度)とする。さらに $\nu$ が $\mu$ に関して絶対連続( $\color{red}\nu \ll \mu$ )とする。このとき， $\mu$ に関して局所可積分な実数値関数(複素数値関数) $f\in L^1_{\mathrm{loc}}(\mu)$ が( $\mu$ –a.e.の意味で)一意的に存在して，

\color{red}\nu(A)=\int_A f \, d\mu,\quad A\in \mathcal{F}

とできる。このときの $f$ を $\color{red} \dfrac{d\nu}{d\mu}$ とかき，ラドンニコディム密度 (Radon-Nikodym density) またはラドンニコディム微分 (Radon-Nikodym derivative) という。

符号付き測度がσ有限とは，測度 $|\nu|=\nu_++\nu_-$ がσ有限であることを指し，複素測度がσ有限とは，符号付き測度 $\operatorname{Re}\nu , \operatorname{Im} \nu$ が共にσ有限であるとします(記号は符号付き測度・複素測度の定義と分解定理内のものを用いた)。

証明は，ジョルダンの分解定理により $\nu$ を分解して考えれば明らかです。