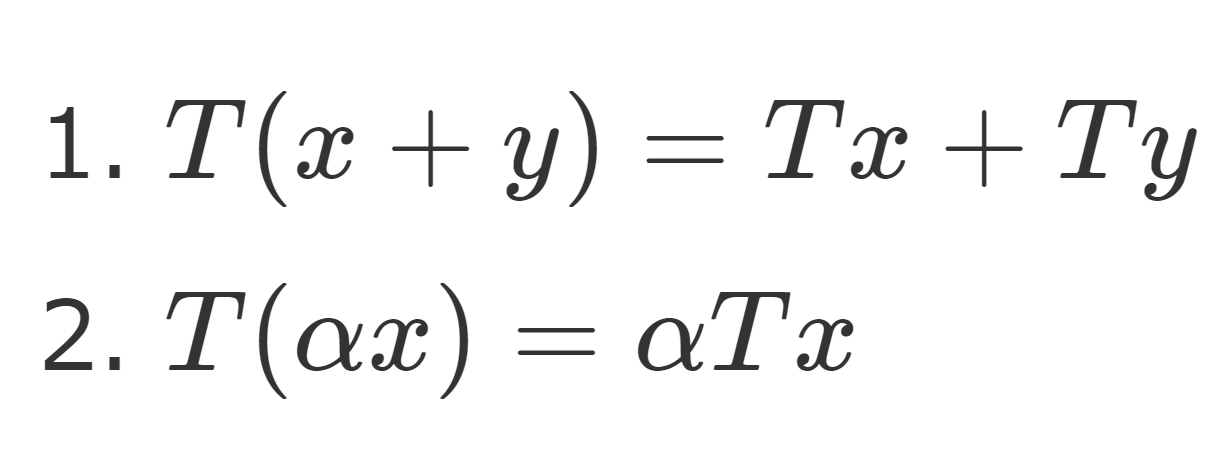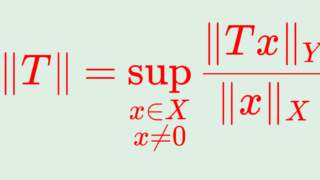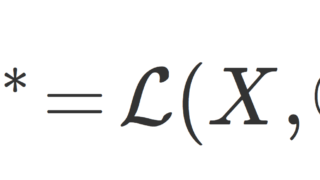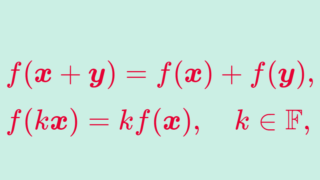線形代数学において,ベクトル空間の間の大事な写像は線形写像ですが,無限次元の線形代数ともいわれる関数解析学では,定義域が空間全体とは限らない「線形作用素」が大事になります。
今回は,そんな線形作用素について定義し,さらに性質の良い「有界線形作用素」について定義と具体例を紹介していきましょう。
線形作用素とは
早速,線形作用素の定義と具体例を紹介しましょう。
線形作用素の定義
定義(線型作用素)
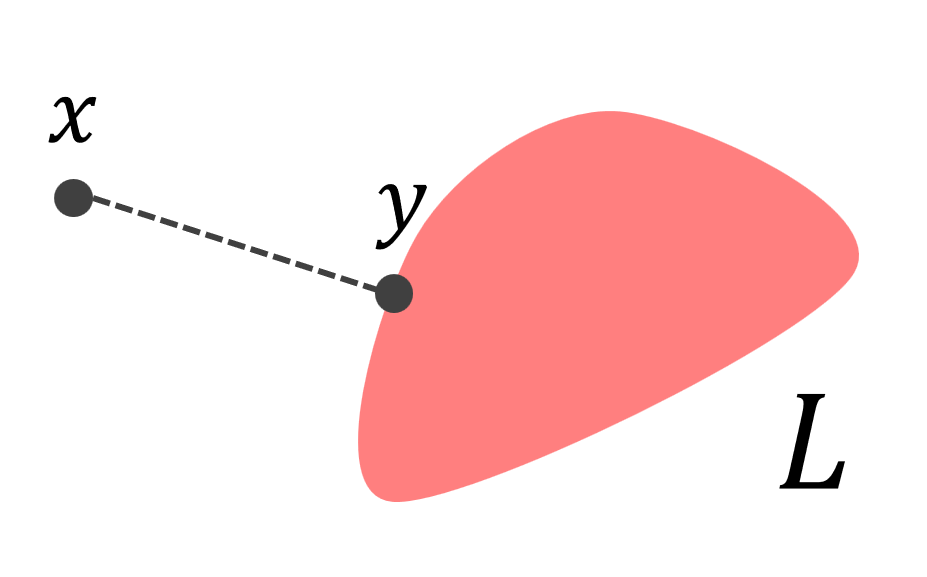
X,Y をベクトル空間とする。このとき, T が X から Y への線形作用素 (linear operator) あるいは単に作用素 (operator) であるとは,ある部分ベクトル空間 A\subset X が存在して, T\colon A\to Y が線形写像になっていることを言う。
このとき, A を T の定義域 (domain) といい, \large \color{red} D(T)=A とかく。また, \{ Tx\mid x\in D(T)\} を値域 (range) といい, \large\color{red} R(T) とかく。
ここでいう,線形写像と線形作用素の違いは,その定義域にあります。 T が X から Y への「線形写像」と言ったときには,定義域は X 全体でなければなりませんが,「線形作用素」と言ったときには,定義域は X の部分空間であればOKです。
線形写像のときと同じですが,「線形」とは,以下が成り立つことを指します。以下, T(x) を Tx と略記します。関数解析においては,勘違いのない場合,括弧は省略するのが普通です。
以下, x,y\in D(T),\; \alpha\in \mathbb{C} とする。以下が成り立つとき,線形 (linear) であるという。
- T(x+y)=Tx+Ty
- T(\alpha x) = \alpha Tx
線形性については,線形写像の定義・性質と具体例8つで詳しく取り扱っています。
なお,単に「作用素」といったときには,線形性を課さないこともありますが,大学課程である関数解析学では,線形作用素のことを意味するのが普通です。
値域 R(T)\subset Y は Y の部分空間になります。
線形作用素の具体例
線形作用素の例(微分作用素)
X を (0,1) 上の実数値関数全体のなすベクトル空間とし,T = \dfrac{d}{dx} を D(T) = C^1(0,1) 上の微分作用素とする。すなわち, f\in D(T) に対し, Tf = f' とする。
この T は X から X の線形作用素である。
関数解析学はよく微分方程式論で用いられますから,上記の例は非常に重要です。
有界線形作用素
線形作用素のうち,有界線形作用素と呼ばれるものは,非常に性質が良く,基本的で重要なものです。紹介していきましょう。
有界線形作用素の定義
定義(有界線形作用素)
X,Y をノルム空間とし, T を X から Y への線形作用素とする。以下の2つが成立するとき, T を有界線形作用素 (bounded linear operator) あるいは単に有界作用素 (bounded operator) という。
- \color{red}\large D(T)=X
- ある M>0 が存在して, \color{red} \large \|Tx\|\le M\|x\| \; (x\in X)
\|Tx\|\le M\|x\| \; (x\in X) の左辺・右辺はそれぞれ X,Y という別の空間のノルムですから,たとえば \|Tx\|_Y\le M\|x\|_X \; (x\in X) のように,ノルムの空間を明示したかき方をした方が丁寧でしょう。
作用素が有界とは,単に2.が成り立つだけではなく,定義域が X 全体になることをいうわけですね。
有界線形作用素の具体例
有界線形作用素の例(積分作用素)
K\colon [0,1]\to \R を有界な連続関数とし, L^1[0,1] を実数値可積分関数 ( \int_0^1|f(x)|\,dx<\infty となる関数) 全体の集合にノルム
\|f\|_1 = \int_0^1|f(x)|\,dx
をいれたバナッハ空間とする。このとき, T\colon L^1[0,1]\to L^1[0,1] を
と定めると, T は有界線形作用素である。
有界線形作用素であることを確認しておきましょう。 K(x) は有界なので, |K(x)|<M\; (0\le x\le 1) となる M>0 を取ります。このとき, f\in L^1[0,1] に対して,
\begin{aligned} \|Tf\|_1 &= \int_0^1 \left| \int_0^{1-x} K(y) f(x+y)\, dy \right|\, dx \\ &\le \int_0^1 \int_0^{1-x} |K(y) f(x+y)|\, dy dx \\ &\le M\int_0^1 \int_0^{1-x} |f(x+y)|\, dy dx \\ &\le M \int_0^1 \|f\|_1 dx \\ &= M \|f\|_1 \end{aligned}
ですから, D(T)=L^1[0,1] かつ \|T f\|_1\le M \|f\|_1 が成り立ちます。よって, T は有界ですね。
有界性と連続性
有界性と密接に関連しているのが連続性です。有界線形作用素は,この「連続性」の性質があるからこそ,非常に重要で扱いやすい概念になっています。
定理(有界性と連続性)
X,Y をノルム空間とし, T を X から Y への線形作用素とする。このとき,次の3つは同値である。
- ある M>0 が存在して,\color{red} \|Tx\|\le M\|x\| \; (x\in D(T))
- T は D(T) 上連続である。すなわち,\color{red} \{ x_n \} \subset D(T),x\in D(T),\; x_n\to x\implies Tx_n \to Tx が成立する。
- T はある一点 y \in D(T) で連続である。すなわち, \color{red} \{ x_n \} \subset D(T), x_n\to y\implies Tx_n\to Ty が成立する。
この定理により,有界線形作用素は,「 D(T)=X かつ性質3.が成り立つもの」だと定義しても良いことになります。
証明しておきましょう。
証明
1.\implies 2.について
\|Tx_n -Tx\|\le M\|x_n-x\|\xrightarrow{n\to\infty} 0 より,すぐわかる。
2. \implies 1.について
背理法で示す。このような M>0 が存在しないとすると,任意の n\ge 1 に対し, x_n \in D(T) が存在して, \|Tx_n\|>n \|x_n\| とできる。 y_n =x_n/\|Tx_n\| とおくと, y_n \in D(T) であり,
\|Ty_n\| =1,\quad \|y_n\| < \frac{1}{n}
となる。右側の式より, n\to\infty とすると, y_n\to 0 となる。これと連続性の仮定2.より, Ty_n \to 0 のはずだが, \|Ty_n\| = 1 に矛盾する。
2.\implies 3.は明らか。
3.\implies 2.について
x\in D(T) とし, x_n\to x となる \{x_n\}\subset D(T) をとる。 T は y\in D(T) で連続なので,
\begin{aligned} Tx_n &= T(x_n -x+y) +T(x-y) \\ &\xrightarrow{n\to\infty} Ty+T(x-y)=Tx\end{aligned}
となり, T は任意の x\in D(T) でも連続である。
証明終
有界線形作用素のなす空間
X,Y をノルム空間とし, X から Y への線形作用素全体の集合を \large \color{red} \mathcal{L}(X,Y) とします。 このとき, \mathcal{L}(X,Y) はベクトル空間になり,さらに作用素の有界性の定義から,各 T\in \mathcal{L}(X,Y) に対し,
\|T\| = \sup_{x\in X\setminus \{0\}} \frac{\|Tx\|}{\|x\|}<\infty
が定まり,これはノルムになります。このノルムを作用素ノルム (operator norm) といいます。したがって, \mathcal{L}(X,Y) はノルム空間になります。特に, X^* = \mathcal{L}(X,\mathbb{C}) のことを双対空間 (dual space) といい, X の性質を調べるために,X^* の性質に着目することも多いです。
この辺については,以下で解説しています。