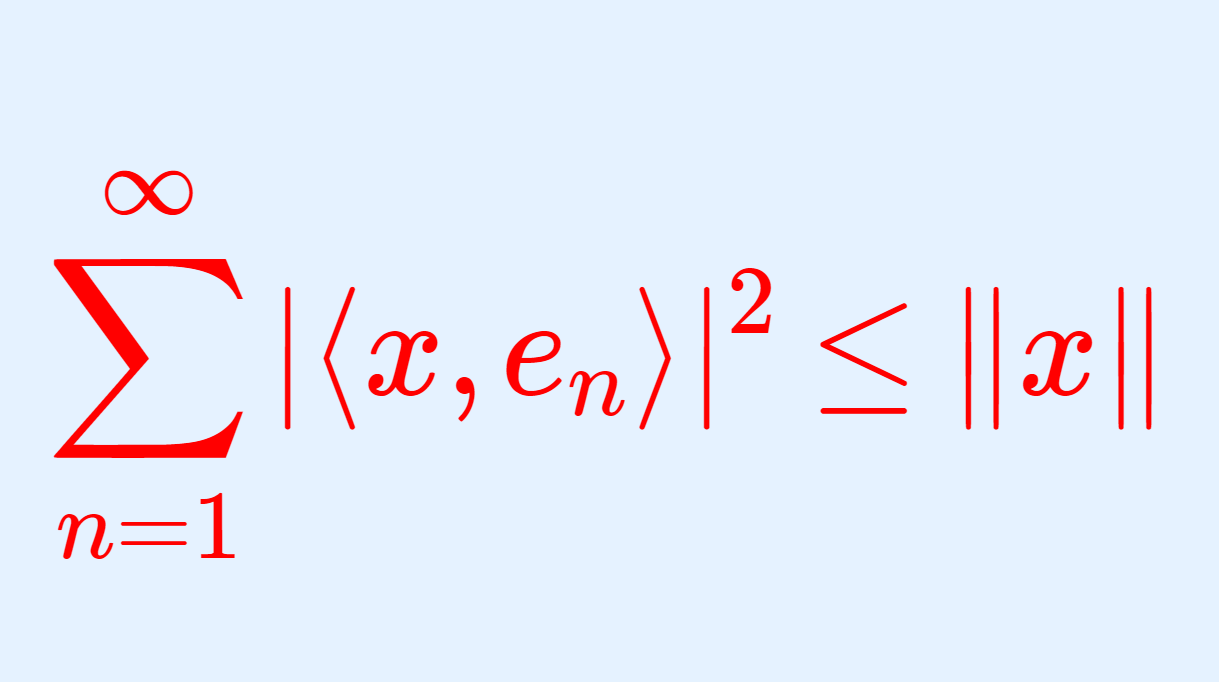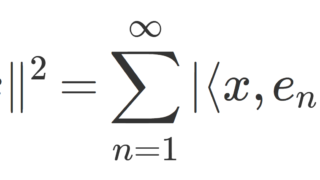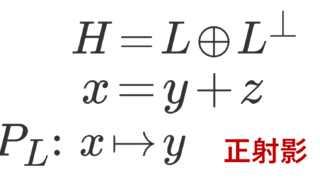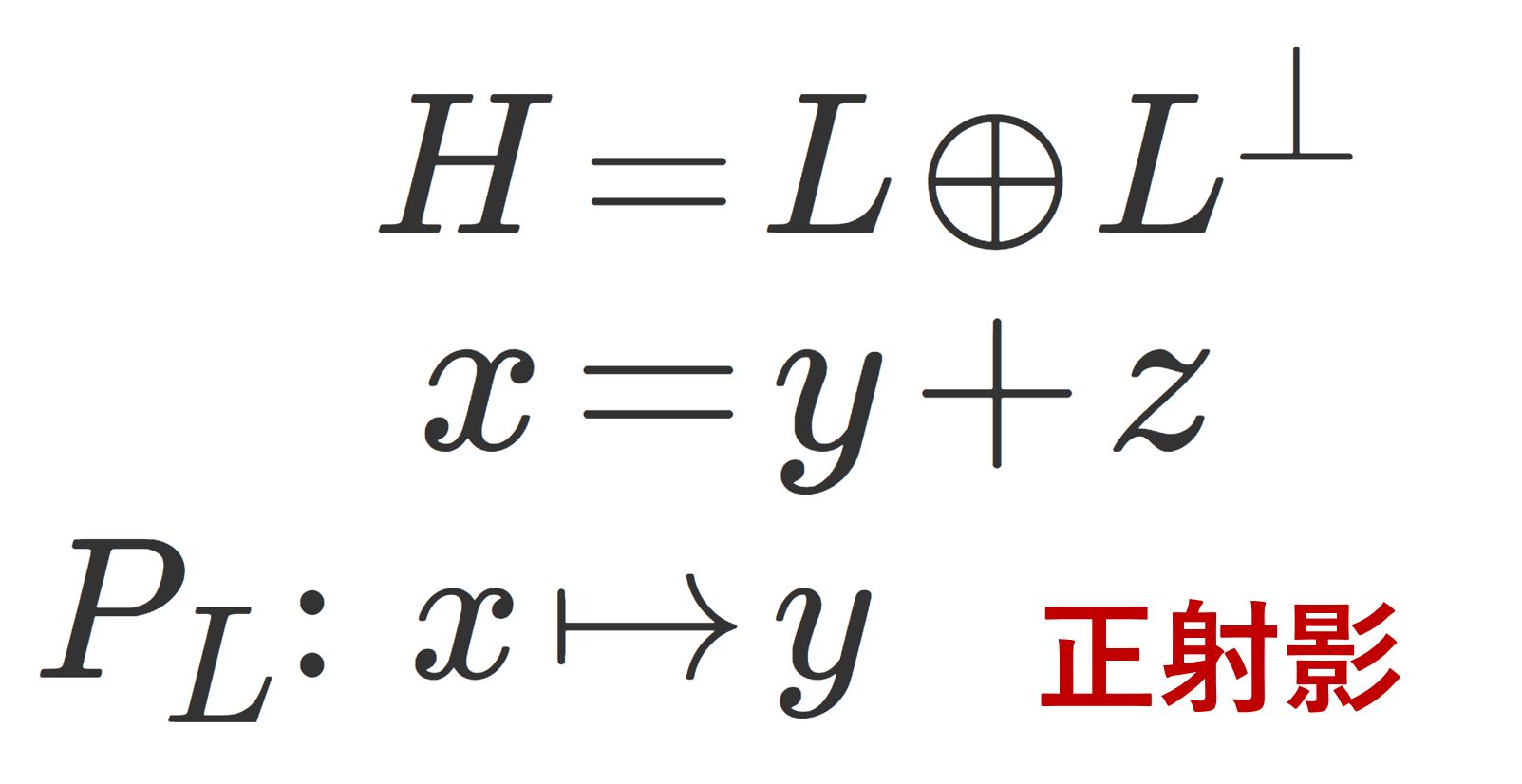ベッセルの不等式とその詳しい証明

内積空間におけるベッセルの不等式 (Bessel’s inequality) は， $\sum_{n=1}^\infty |\langle x, e_n\rangle |^2\le \| x\|$ という不等式のことです。それぞれの意味をきちんと説明し，さらにベッセルの不等式を証明しましょう。

ベッセルの不等式とその詳しい証明
発展～パーセバルの等式～
関連する記事

ベッセルの不等式とその詳しい証明

以下で， $\{ e_n\}$ が正規直交系 (orthonormal system) であるとは， $\langle e_n,e_m\rangle = \begin{cases} 1 & n=m, \\ 0 & n\ne m \end{cases}$ すなわち，互いに直交する大きさ $1$ のベクトルの集まりということです(→正規直交系・正規直交基底)。

定理1（ベッセルの不等式; Bessel’s inequality）

$X$ を内積空間， $\{e_n\}_{n=1}^\infty\subset X$ を正規直交系とする。このとき，任意の $x\in X$ に対して，

\color{red} \Large \sum_{n=1}^\infty |\langle x, e_n\rangle |^2\le \| x\|

が成り立つ。

なお，本定理は $\sum_{n=1}^m |\langle x, e_n\rangle |^2\le \| x\|$ のように左辺が有限和であっても全く同様に成立します。

証明を添付しておきましょう。内積が扱えれば，多くの知識なしで証明可能です。

証明

任意の整数 $m\ge 1$ に対して，

\begin{aligned}0&\le \Bigl\| x-\sum_{n=1}^m \langle x, x_n\rangle e_n \Bigr\|^2 \\ & =\|x\|^2-\Bigl\langle x,\sum_{n=1}^m \langle x, e_n\rangle e_n\Bigr\rangle \\ & \quad -\Bigl\langle \sum_{n=1}^m \langle x, e_n\rangle e_n, x\Bigr\rangle+\Bigl\|\sum_{n=1}^m \langle x, e_n\rangle e_n \Bigr\| ^2\end{aligned}

である。ここで，

\begin{aligned}\Bigl\langle x,\sum_{n=1}^m \langle x, e_n\rangle e_n\Bigr\rangle &=\overline{\sum_{n=1}^m \langle x, e_n\rangle } \langle x, e_n\rangle \\ &= \sum_{n=1}^m |\langle x, e_n\rangle|^2,\\ \Bigl\langle \sum_{n=1}^m \langle x, e_n\rangle e_n, x\Bigr\rangle&= \sum_{n=1}^m \langle x,e_n\rangle \langle e_n, x\rangle \\ &= \sum_{n=1}^m |\langle x, e_n\rangle|^2, \\ \Bigl\|\sum_{n=1}^m \langle x, e_n\rangle e_n \Bigr\| &=\sum_{n=1}^m |\langle x, e_n\rangle|^2 \end{aligned}

なので，結局，最初の式は

\begin{aligned}0&\le \Bigl\| x-\sum_{n=1}^m \langle x, e_n\rangle e_n \Bigr\|^2 \\ &= \|x\|^2-\sum_{n=1}^m |\langle x,e_n\rangle|^2 \end{aligned}

となる。したがって， $\sum_{n=1}^m |\langle x,e_n\rangle|^2\le \|x\|^2$ であり， $m\to\infty$ とすることで， $\sum_{n=1}^\infty |\langle x,e_n\rangle|^2\le \|x\|^2$ である。

証明終

発展～パーセバルの等式～

完備な内積空間であるヒルベルト空間においては，もう一段「強い」定理が成立します。以下で， $\{ e_n\}$ が正規直交基底 (orthonormal basis) であるとは， $\{e_n\}$ が正規直交系かつ $\overline{\operatorname{Span} \{e_n\}}$ が空間全体となることを言います(→正規直交系・正規直交基底)。

定理2（パーセバルの等式; Parseval’s equality）

$H$ をヒルベルト空間， $\{e_n\}_{n=1}^\infty\subset H$ を正規直交基底とする。このとき，任意の $x\in H$ に対して，

\color{red} \Large \sum_{n=1}^\infty |\langle x, e_n\rangle |^2= \| x\|

が成り立つ。

これは，三平方の定理（ピタゴラスの定理）の無限次元バージョンということができます。

この定理の証明は，ヒルベルト空間における正射影の話が必要であり，難易度が少々上がります。証明は以下で行っています。

ただ，この定理と正射影の話を既知とすると，ヒルベルト空間におけるベッセルの不等式はパーセバルの等式の劣化版ともいえる公式です。実際，正規直交系 $\{e_n\}$ のなす閉部分空間を $L=\overline{\operatorname{Span}\{e_n\}}$ とし， $x\in H$ の $L$ への正射影を $x_L$ とかくとすると，