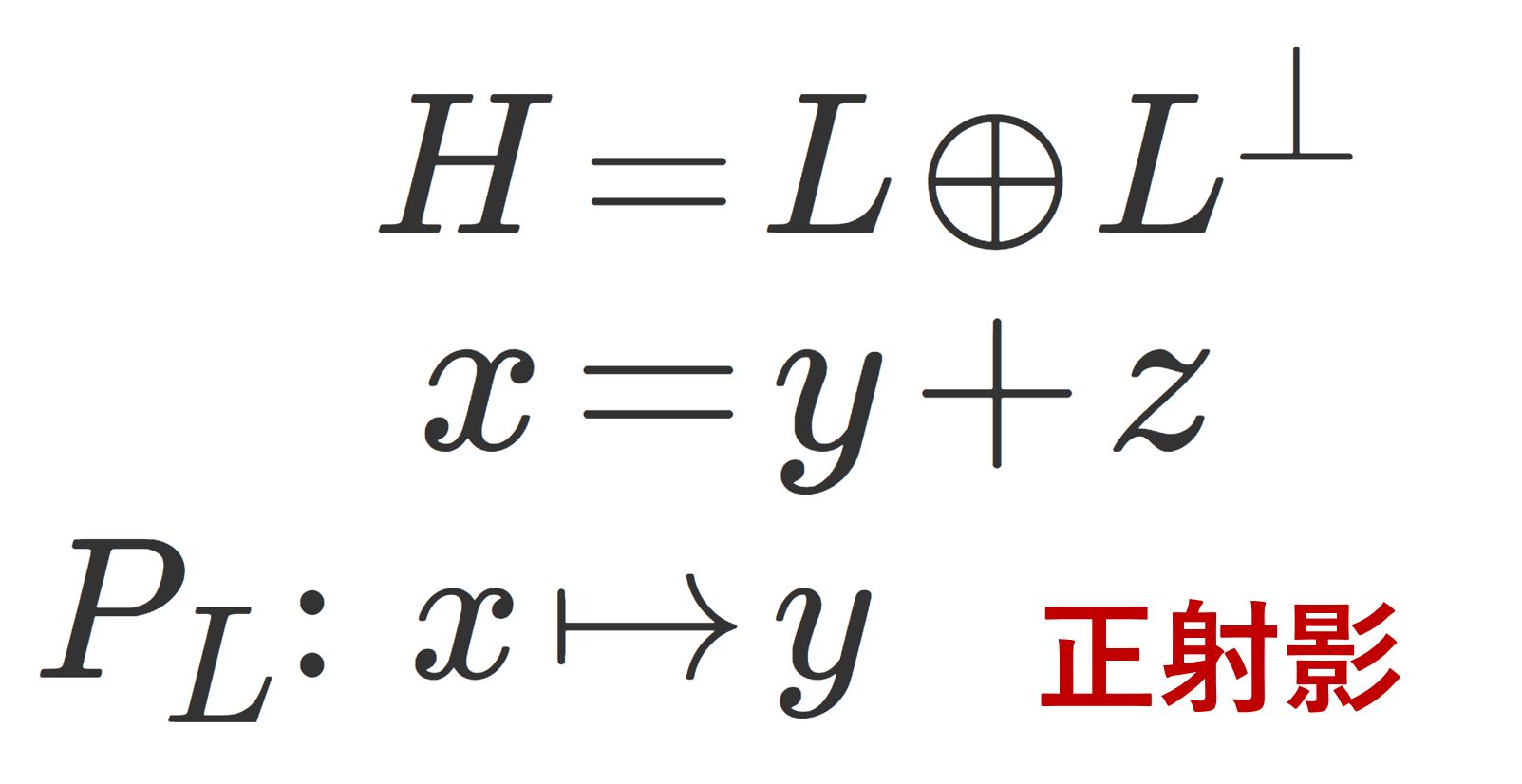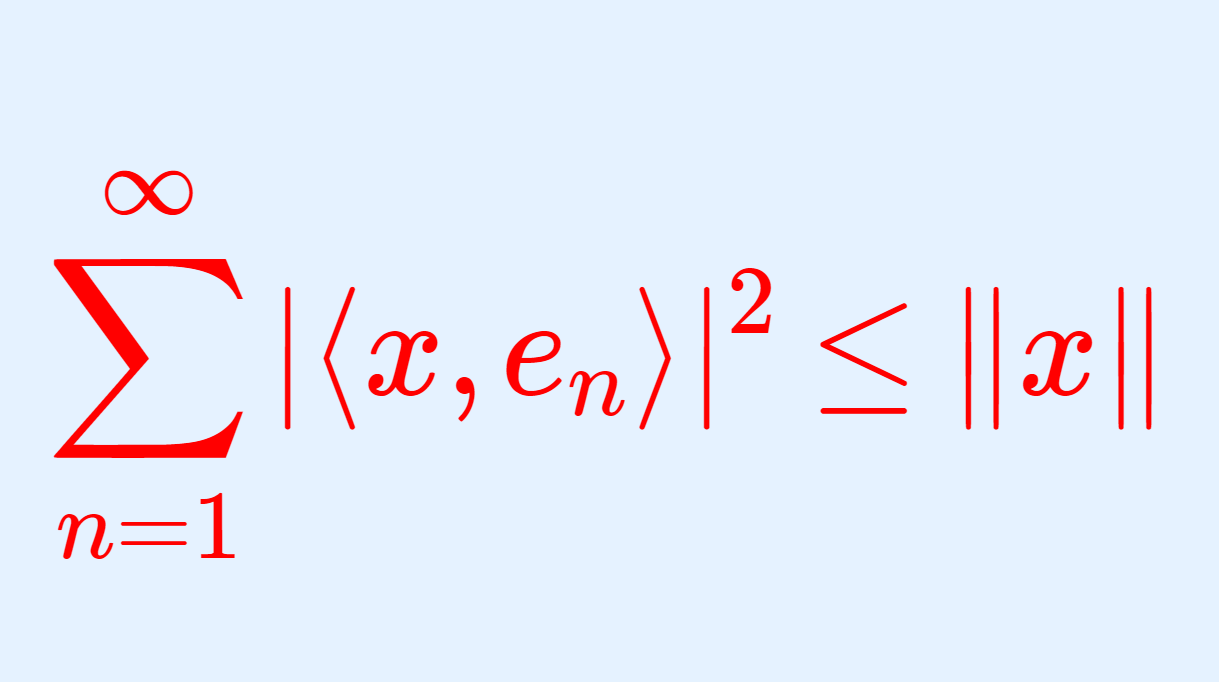PR

ヒルベルト空間における正射影・正射影作用素

2022.10.31
関数解析学
用語・記号の定義大学専門
記事内に広告が含まれています。

ヒルベルト空間における正射影あるいは直交射影について，その定義を紹介し，関連して正規直交系が与えられた部分空間上への射影について考えましょう。

正射影作用素

ヒルベルト空間は「射影定理」という重要な定理があり，その性質を用いて正射影が定義されます。まずは射影定理を復習しておきましょう。

ヒルベルト空間上の射影定理

H H をヒルベルト空間，L⊂H L\subset H をその閉部分空間とする。このとき，

L⊥={x∈H∣∀a∈L,⟨x,a⟩=0} L^\perp= \{ x\in H\mid \forall a\in L, \langle x,a \rangle =0\}


を L⊥ L^\perp を L L の直交補空間とすると，H=L⊕L⊥ \large \color{red} H = L\oplus L^\perp である。すなわち，任意の x∈H x\in H に対し，

x=y+z,y∈L,z∈L⊥\large \color{red} x=y+z, \quad y\in L, z\in L^\perp


と，一意的に分解できる(→ベクトル空間の直和)。

ヒルベルト空間は，直交する二つの部分空間の「足し算」と分けることができるという定理です。詳しくは，ヒルベルト空間における射影定理とその証明で解説しています。これを用いると，正射影が定義可能です。

定義（正射影）

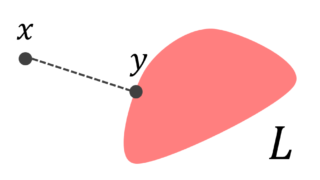
上の射影定理において，y y を，x x の正射影 (orthogonal projection; 直交射影) といい，xx に対し，y y を対応させる写像 PL ⁣:H→L P_L\colon H\to L を H H における L L の上への(正)射影作用素 (orthogonal projection; 直交射影作用素) という。

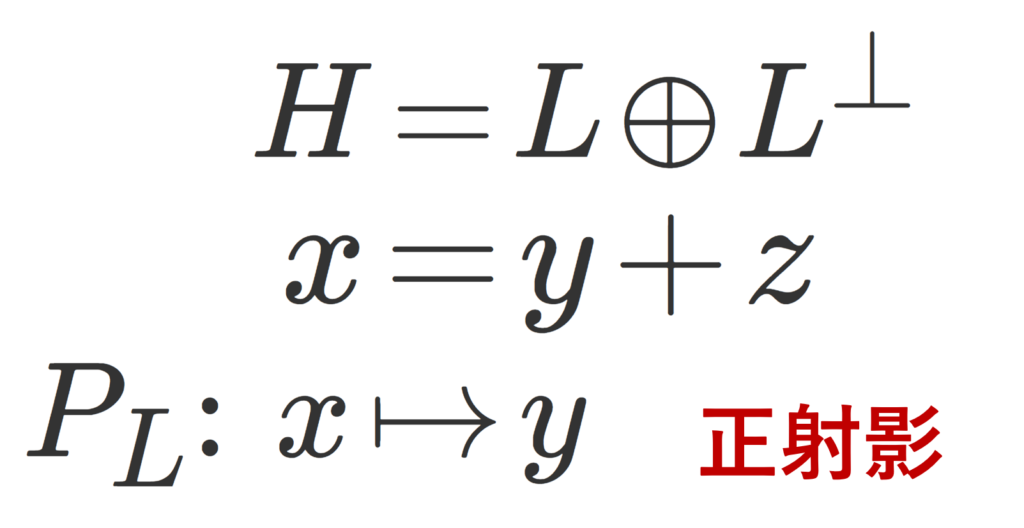
射影定理と正射影

x∈Lx\in L は x=x+0  (x∈L,0∈L⊥) x=x+0\; (x\in L, 0\in L^\perp) ですから，射影作用素は明らかに全射であり，(PL)2=PL (P_L)^2=P_L が成立します。

また，x∈H=L⊕L⊥ x\in H=L\oplus L^{\perp} に対し，z∈L⊥z\in L^\perp を対応させる射影作用素 PL⊥ P_{L^{\perp}} は，z=x−y  (y∈L) z=x-y\;(y\in L) から PL⊥=I−PL P_{L^{\perp} }=I-P_L とかけます(I I は恒等写像)。以上は，以下の定理の1,2.にあたります。

定理1（射影作用素の性質）

  1. (PL)2=PL \large (P_L)^2=P_L
  2. PL⊥=I−PL \large P_{L^\perp} = I-P_L
  3. PL∗=PL\large P_L^*=P_L

3. のPL∗ P_L^* は PL P_L の共役作用素です。(正)射影作用素は自己共役であるということですね。3.について証明しておきましょう。

まず，x,x′∈H x,x'\in H を x=y+z, x′=y′+z′∈L⊕L⊥ x=y+z,\, x'=y'+z' \in L\oplus L^\perp とします。すると，PLx=x′, PLx′=y′ P_L x=x',\, P_Lx' = y' であり，L⊥L⊥ L\perp L^\perp なので，

⟨PLx,x′⟩=⟨y,y′+z′⟩=⟨y,y′⟩=⟨y+z,y′⟩=⟨x,PLx′⟩ \begin{aligned}\langle &P_L x,x'\rangle =\langle y, y'+z'\rangle = \langle y, y' \rangle \\&= \langle y+z, y'\rangle = \langle x, P_Lx'\rangle\end{aligned}


となり，これは PL∗=PL P_L^*=P_L を意味していますね。

正規直交系への射影

正射影と関連する話題として，正規直交系が張る空間への正射影を考えましょう。

定理2（正規直交系への射影）

H H をヒルベルト空間，{en}n=1∞⊂H \{e_n\}_{n=1}^\infty\subset H を正規直交系とする。また，H H の閉部分空間 L L を L=Span⁡{en}n=1∞‾ L=\overline{\operatorname{Span} \{e_n\}_{n=1}^\infty} と定める(→Spanの意味とは【線形結合】)。このとき，任意の x∈Hx\in H に対して L L への射影 PLx P_Lx は

PLx=∑n=1∞⟨x,en⟩en\color{red} \Large \begin{equation}P_Lx = \sum_{n=1}^\infty \langle x, e_n\rangle e_n \end{equation}


と表せる。また，x,y∈H x,y\in H に対し，

⟨PLx,PLy⟩=∑n=1∞⟨x,en⟩⟨y,en⟩‾\color{red}\begin{equation}\langle P_Lx,P_Ly\rangle =\sum_{n=1}^\infty \langle x, e_n \rangle \overline{ \langle y, e_n\rangle} \end{equation}


も成り立つ。

(1) (1) 式の無限和の収束は当然「H H のノルムの意味で」です。すなわち，

∥PLx−∑n=1N⟨x,en⟩en∥→N→∞0\left\|P_Lx - \sum_{n=1}^N \langle x, e_n\rangle e_n\right\| \xrightarrow{N\to\infty}0


の意味です。一方で，(2) (2) 式は複素数和の収束の意味です。

特に，{en}n \{e_n\}_n が正規直交基底のとき，すなわち Span⁡{en}n=1∞‾=H \overline{\operatorname{Span} \{e_n\}_{n=1}^\infty}=H のときは，以下が成立します。

定理2の系（正規直交基底を用いた分解）

H H をヒルベルト空間とし，{en}n=1∞⊂H \{e_n\}_{n=1}^\infty\subset H をその正規直交基底とする。このとき，任意の x∈Hx\in H に対して，

x=∑n=1∞⟨x,en⟩en\color{red} \Large \begin{equation}x = \sum_{n=1}^\infty \langle x, e_n\rangle e_n \end{equation}


と直交分解できる。

また，x,y∈H x,y\in H に対し，

⟨x,y⟩=∑n=1∞⟨x,en⟩⟨y,en⟩‾\color{red}\begin{equation}\langle x,y\rangle =\sum_{n=1}^\infty \langle x, e_n \rangle \overline{ \langle y, e_n\rangle} \end{equation}


も成り立つ。

なお，{en}n=1∞⊂H \{e_n\}_{n=1}^\infty\subset H とかきましたが，定理2とその系は非可算無限個の正規直交系(基底)を持つ場合 ({eλ}λ∈Λ⊂H \{e_\lambda\}_{\lambda\in \Lambda} \subset H ) も成立します。非可算無限個の正規直交基底を持つ場合，x∈H x\in H に対し，⟨x,eλ⟩≠0 \langle x, e_\lambda \rangle \ne 0 となる λ \lambda は高々可算個しかないので，PLx=∑λ∈Λ⟨x,eλ⟩eλ P_Lx = \sum_{\lambda\in \Lambda} \langle x, e_\lambda \rangle e_\lambda は結局可算和になって同様です。

念のため，⟨x,eλ⟩≠0 \langle x, e_\lambda \rangle \ne 0 となる λ \lambda 全体の集合 F F は高々可算個しかないことを確認しておきましょう。ベッセルの不等式より，任意の有限集合 S⊂Λ S\subset \Lambda に対して，∑λ∈S∣⟨x,eλ⟩∣2≤∥x∥2 \sum_{\lambda\in S} |\langle x, e_\lambda\rangle |^2\le \|x\|^2 です。よって ∣⟨x,eλ⟩∣2≥∥x∥2/n |\langle x, e_\lambda \rangle|^2 \ge \|x\|^2/n となる λ \lambda の集合 FnF_n は高々 n n の要素しか持ちません。

F=⋃n=1∞Fn F = \bigcup_{n=1}^\infty F_n


ですから，F F は高々可算個ですね。

正規直交系への射影の証明

早速定理を証明していきます。念のため，定理を再掲しておきます。

定理2（正規直交系への射影）再掲

H H をヒルベルト空間，{en}n=1∞⊂H \{e_n\}_{n=1}^\infty\subset H を正規直交系とする。また，H H の閉部分空間 L L を L=Span⁡{en}n=1∞‾ L=\overline{\operatorname{Span} \{e_n\}_{n=1}^\infty} と定める(→Spanの意味とは【線形結合】)。このとき，任意の x∈Hx\in H に対して L L への射影 PLx P_Lx は

PLx=∑n=1∞⟨x,en⟩en\color{red} \Large \begin{equation}P_Lx = \sum_{n=1}^\infty \langle x, e_n\rangle e_n \end{equation}


と表せる。また，x,y∈H x,y\in H に対し，

⟨PLx,PLy⟩=∑n=1∞⟨x,en⟩⟨y,en⟩‾\color{red}\begin{equation}\langle P_Lx,P_Ly\rangle =\sum_{n=1}^\infty \langle x, e_n \rangle \overline{ \langle y, e_n\rangle} \end{equation}


も成り立つ。

証明は長めですが，やっていること自体はシンプルで，方針が分かりやすいと思います。

証明

PLx=∑n=1∞⟨x,en⟩enP_Lx = \sum_{n=1}^\infty \langle x, e_n\rangle e_n について

まず，∑n=1∞⟨x,en⟩en \sum_{n=1}^\infty \langle x, e_n\rangle e_n が収束することを示す。ym=∑n=1m⟨x,en⟩en y_m =\sum_{n=1}^m \langle x, e_n\rangle e_n とおく。 m>lm>l に対して，

∥ym−yl∥2=∥∑n=l+1m⟨x,en⟩en∥2=∑n=l+1m∣⟨x,en⟩∣2\begin{aligned}\|y_m-y_l \|^2 &=\left\|\sum_{n=l+1}^m \langle x, e_n\rangle e_n\right\|^2\\ &= \sum_{n=l+1}^m |\langle x, e_n\rangle|^2 \end{aligned}


である。ベッセルの不等式より，∑n=1∞∣⟨x,en⟩∣2≤∥x∥<∞ \sum_{n=1}^\infty |\langle x, e_n\rangle|^2 \le \|x\|<\infty であるから，特に ∑n=l+1m∣⟨x,en⟩∣2→l,m→∞0 \sum_{n=l+1}^m |\langle x, e_n\rangle|^2 \xrightarrow{l,m\to\infty} 0 となる。したがって，{ym}m \{y_m\}_m はコーシー列である。ヒルベルト空間は完備であるから，

xL=lim⁡m→∞ym=∑n=1∞⟨x,en⟩enx_L =\lim_{m\to\infty} y_m =\sum_{n=1}^\infty \langle x, e_n\rangle e_n


は収束する。ym∈L y_m\in L であるから，xL∈L x_L\in L である。m>nm>n のとき，⟨ym,en⟩=⟨x,en⟩ \langle y_m ,e_n\rangle=\langle x ,e_n\rangle であるから，

⟨x−xL,en⟩=⟨x,en⟩−⟨xL,en⟩=⟨x,en⟩−lim⁡m→∞⟨ym,en⟩=⟨x,en⟩−⟨x,en⟩=0\begin{aligned}\langle x-x_L, e_n\rangle &= \langle x,e_n\rangle - \langle x_L, e_n\rangle\\ &= \langle x,e_n\rangle -\lim_{m\to\infty} \langle y_m ,e_n\rangle \\ &=\langle x,e_n\rangle - \langle x ,e_n\rangle \\ &= 0 \end{aligned}


である(2つ目の等式は内積の連続性を用いた)。任意の n≥1 n\ge 1 に対し x−xL⊥en x-x_L\perp e_n がわかる。したがって，x−xL∈L⊥ x-x_L\in L^\perp (L L の直交補空間)である。ゆえに，

x=xL+(x−xL)x = x_L+(x-x_L)


は H=L⊕L⊥ H=L\oplus L^\perp の分解に相当している。したがって，PLx=xL P_L x = x_L であり，示された。

⟨PLx,PLy⟩=∑n=1∞⟨x,en⟩⟨y,en⟩‾\langle P_Lx,P_Ly\rangle =\sum_{n=1}^\infty \langle x, e_n \rangle \overline{ \langle y, e_n\rangle} について

コーシーシュワルツの不等式より，

∑n=1∞∣⟨x,en⟩⟨y,en⟩‾∣≤(∑n=1∞∣⟨x,en⟩∣2)1/2(∑n=1∞∣⟨y,en⟩∣2)1/2\begin{aligned}&\sum_{n=1}^\infty|\langle x,e_n\rangle\overline{\langle y, e_n \rangle}|\\ &\le \left(\sum_{n=1}^\infty |\langle x,e_n\rangle|^2\right)^{1/2} \left( \sum_{n=1}^\infty |\langle y,e_n\rangle|^2 \right)^{1/2}\end{aligned}


である。ベッセルの不等式より，右辺は有限であるから，∑n=1∞∣⟨x,en⟩⟨y,en⟩‾∣ \sum_{n=1}^\infty|\langle x,e_n\rangle\overline{\langle y, e_n \rangle}| は絶対収束する。ここで，

⟨∑n=1m⟨x,en⟩en,∑n=1m⟨y,en⟩en⟩=∑n=1m⟨x,en⟩⟨en,∑k=1m⟨y,ek⟩ek⟩=∑n=1m⟨x,en⟩⟨y,en⟩‾ \begin{aligned}&\left\langle \sum_{n=1}^m \langle x,e_n\rangle e_n, \sum_{n=1}^m \langle y, e_n \rangle e_n\right\rangle\\ &= \sum_{n=1}^m \langle x,e_n\rangle \left\langle e_n, \sum_{k=1}^m \langle y, e_k \rangle e_k\right\rangle\\ &= \sum_{n=1}^m \langle x,e_n\rangle\overline{\langle y, e_n \rangle} \end{aligned}

である。これと内積の連続性により，

∑n=1∞⟨x,en⟩⟨y,en⟩‾=lim⁡m→∞∑n=1m⟨x,en⟩⟨y,en⟩‾=lim⁡m→∞⟨∑n=1m⟨x,en⟩en,∑n=1m⟨y,en⟩en⟩=⟨∑n=1∞⟨x,en⟩en,∑n=1∞⟨y,en⟩en⟩=⟨PLx,PLy⟩ \begin{aligned}&\sum_{n=1}^\infty \langle x,e_n\rangle\overline{\langle y, e_n \rangle}\\ &=\lim_{m\to\infty} \sum_{n=1}^m \langle x,e_n\rangle\overline{\langle y, e_n \rangle} \\ &=\lim_{m\to\infty}\left\langle \sum_{n=1}^m \langle x,e_n\rangle e_n, \sum_{n=1}^m \langle y, e_n \rangle e_n\right\rangle \\ &= \left\langle \sum_{n=1}^\infty \langle x,e_n\rangle e_n, \sum_{n=1}^\infty \langle y, e_n \rangle e_n\right\rangle \\ &= \langle P_Lx, P_L y\rangle \end{aligned}


であるから，題意は示された。

証明終

長かったかもしれませんが，無事証明できましたね。

正射影を利用して正規直交系を作る

ここまで，正規直交系への正射影を解説してきましたが，逆に正射影を活用することで，正規直交系を作ることも可能です。これを，グラムシュミットの直交化法 (Gram–Schmidt process) といいます。以下で解説しています。

グラムシュミットの直交化法とは～イメージを図解～
グラムシュミットの直交化法 (Gram–Schmidt process) あるいは単にシュミットの直交化法とは，与えられた基底を用いて，正規直交基底を具体的に構成する手法です。グラムシュミットの直交化法について，その手法とイメージの図解を紹介します。
mathlandscape.com

関連する記事

ヒルベルト空間における射影定理とその証明
ヒルベルト空間において非常に基本的な定理である射影定理 (projection theorem) について，その定理の主張と証明を行いましょう。
mathlandscape.com
正規直交系・正規直交基底
正規直交系とは，大きさが1であり，互いに直交するベクトルの集まりを指します。また，正規直交基底(完全正規直交系)とは，正規直交系で，かつ全てのベクトルがそれらを用いて表現可能なことをいいます。正規直交系・正規直交基底について，定義と具体例を見ていきましょう。
mathlandscape.com