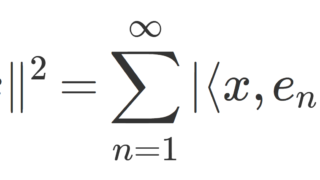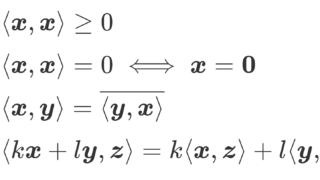正規直交系とは,大きさが1であり,互いに直交するベクトルの集まりを指します。また,正規直交基底(完全正規直交系)とは,正規直交系で,かつ全てのベクトルがそれらを用いて表現可能なことをいいます。
正規直交系・正規直交基底について,定義と具体例を見ていきましょう。
正規直交系・正規直交基底とは
正規直交系とは
定義(正規直交系)
X を内積空間とする。 \{e_n\} \subset X\setminus\{0\} が直交系 (orthogonal system) であるとは,
\color{red}\large m\ne n\implies \langle e_m , e_n\rangle =0
が成り立つことをいい,加えて任意の n について
が成り立つとき, \{e_n\} は正規直交系 (orthonormal system; ONS) であるという。
添え字には n を用いたが, \{e_n\}\subset X\setminus\{0\} は有限集合・可算集合・非可算集合のいずれでもよいことに注意する。
\|e_n\| = \sqrt{\langle e_n,e_n\rangle} ですから,正規直交系の定義は単に
\color{red}\Large \langle e_m , e_n\rangle = \delta_{mn}
と書いても同じです。ただし, \delta_{mn} はクロネッカーのデルタを指します。
直交系 \{ x_n\} が与えられたとき, \{x_n/\|x_n\|\} は正規直交系になります。
ここで,正規直交系は一次独立です。実際, \{e_n\} を正規直交系とし,その中から任意に有限個 e_{j_1}, e_{j_2},\dots, e_{j_m} を持ってきて, k_1,k_2,\dots, k_m\in\mathbb{C}\text{ (or }\mathbb{R}) に対し,
k_1e_{j_1}+k_2 e_{j_2}+\dots +k_m e_{j_m}=0
とします。 1\le i\le m に対し,等式の両辺 e_{j_i} と内積を取ると,
がわかります。任意の 1\le i\le m でこれが成立するため,結局 k_1=k_2=\dots=k_m=0 となって,確かに正規直交系は一次独立です。
正規直交基底とは
定義(正規直交基底)
X を内積空間とする。 \{e_n\}\subset X が正規直交系であり,かつ \color{red}\overline{\operatorname{Span} \{e_n\}}=X が成り立つとき, \{e_n\} は正規直交基底 (orthonormal basis; ONB) または完全正規直交系 (complete orthonormal system; CONS) という。
ただし, \operatorname{Span} とは
\begin{aligned}&\operatorname{Span} \{e_n\}\\&= \left\{ \sum_{i=1}^m k_i {e_{j_i}} \middle| k_1,\dots, k_m \in \mathbb{C}\text{ (or }\mathbb{R}),\; m\ge 1 \right\} \end{aligned}
は, \{e_n\} のうち,有限個の一次結合全体の集合のなす部分ベクトル空間であり(→Spanの意味とは【線形結合】),上付きのバーはその閉包を指す。
内積空間上で定義しましたが,完備な内積空間である「ヒルベルト空間」上で考えることが多いです。
正規直交「基底」と言っていますが,特に無限次元の場合は,一般的なベクトル空間で定義される標準的な意味での「基底」とは違います。
本来, S\subset V が一般のベクトル空間 V の基底 (basis) であるとは, S が一次独立であり,かつ V の任意の元が, S の有限個の一次結合で書ける,というものでした。後者を言い換えると, \operatorname{Span} S=V でなければなりません。
今回は \overline{\operatorname{Span} \{e_n\}}=V のように,閉包を取っていますから, V の任意の元が \{e_n\} のうちの有限個の一次結合で「近似」できればOKということです。
一般的なベクトル空間とは違い,内積空間には距離の概念(収束の概念)があるため,「閉包をとる」操作を含むような定義もできるわけです。
正規直交系・正規直交基底の例
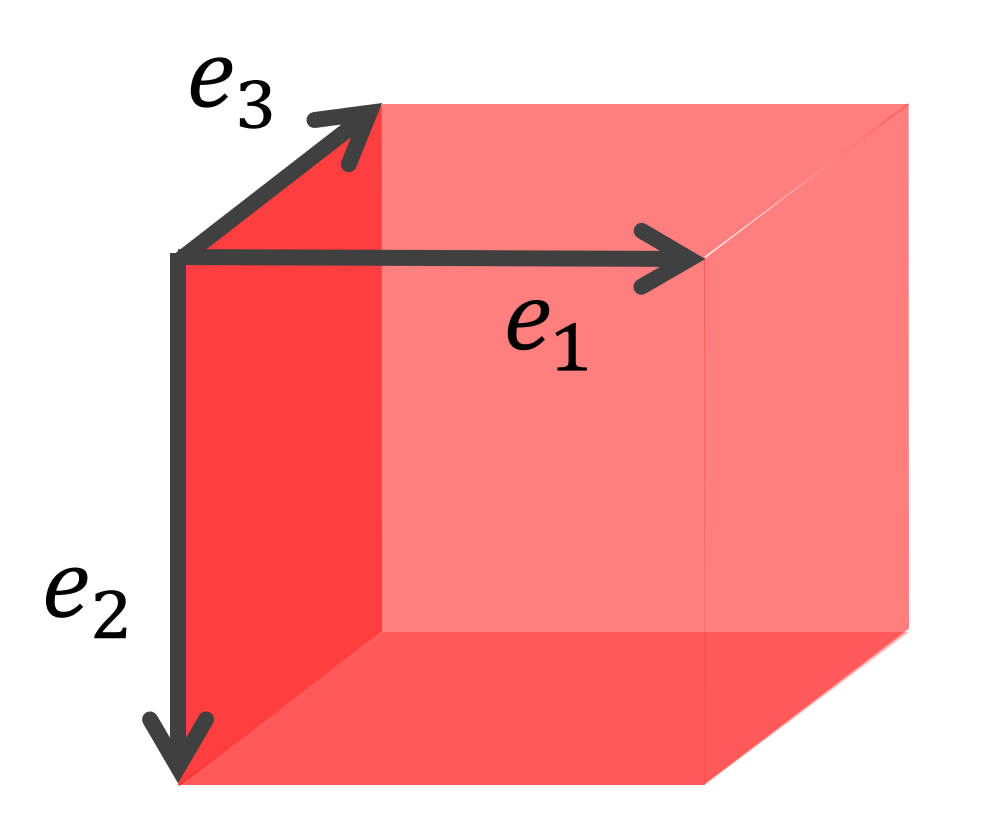
例1 ( \mathbb{C}^n ).
\mathbb{C} 上の内積空間(ヒルベルト空間) \mathbb{C}^n において,
\begin{aligned} e_1 &= (1,0,0,\dots,0), \\ e_2&= (0,1,0,\dots,0),\\ &\;\vdots \\ e_n &=(0,0,0,\dots, 1) \end{aligned}
とすると,\{e_k\}_{k=1}^n は正規直交基底になる。
a=(a_1,\dots, a_n), \, b=(b_1,\dots, b_n)\in\mathbb{C}^n に対し,内積が
\langle a,b\rangle =a_1\overline{b_1}+\dots+a_1n\overline{b_n}
と定義される内積空間 \mathbb{C}^n ですね。これは有限次元ベクトル空間であり,正規直交基底でいう「基底」は一般のベクトル空間における「基底」と同じ意味です。
なお,\R 上の内積空間 \R^n でも同様です。
例2 ( \ell^2 ).
\ell^2 を \sum_{n=1}^\infty |a_n|^2<\infty となる数列全体の集合とする。
\begin{aligned} e_1 &= (1,0,0,\dots,0), \\ e_2&= (0,1,0,\dots,0),\\ &\;\vdots \\ \end{aligned}
とすると,\{e_n\}_{n=1}^\infty は正規直交基底になる。
a=(a_n),\; b=(b_n)\in \ell^2 に対し, \langle a,b\rangle =\sum a_n\overline{b_n} と定義される内積空間(ヒルベルト空間)です。
ここでいう正規直交「基底」は,一般のベクトル空間における「基底」とは違います。たとえば, a_n = 1/n となる数列 a=(a_n)\in\ell^2 は, \{e_n\} の有限和ではかけませんが,
a=\sum_{n=1}^\infty \frac{1}{n} e_n
とかけるため「有限和の近似」で表すことはできますね。右辺は \lim_{m\to\infty} \sum_{n=1}^m の意味ですが, \lim の収束は当然 \ell^2 の位相の意味です。
例3 ( L^2[0,1] ).
L^2[0,1] を, \int_0^1 |f(x)|^2\,dx<\infty となる可測関数 f\colon [0,1]\to \mathbb{C} 全体(をa.e.で同一視した)のなすヒルベルト空間とする。
このとき, e_n(x)=e^{2\pi i nx} と定めると, \{e_n\}_{n\in\mathbb{Z}} は正規直交基底になる。
f,g\in L^2[0,1] に対し, \langle f,g\rangle =\int_0^1 f(x)\overline{g(x)}\,dx と定義されるヒルベルト空間です。
フーリエ級数展開に関連する話です。正規直交「基底」であることは難しいですが,正規直交系であることは簡単にわかるので,確認してみてください。
正規直交系と三平方の定理(ピタゴラスの定理)
正規直交系においては,三平方の定理(ピタゴラスの定理)が成立します。それが以下の定理です。
定理(正規直交系の三平方の定理)
X を内積空間, \{e_k\}_{k=1}^n \subset X を正規直交系とする。このとき, a_k \in \mathbb{C}\; (1\le k\le n) に対し,
\color{red}\Bigl\| \sum_{k=1}^n a_k e_k\Bigr\|^2 = \sum_{k=1}^n |a_k|^2
が成り立つ。
実質「三」平方ではありませんが,ニュアンスが伝わればOKです。
簡単に証明しておきましょう。
証明
内積の第一成分に関する線形性,第二成分に関する共役線形性より,
\begin{aligned} \Bigl\| \sum_{k=1}^n a_k e_k\Bigr\|^2 &= \Bigl\langle\sum_{k=1}^n a_k e_k,\sum_{k=1}^n a_k e_k \Bigr\rangle \\ &=\sum_{k,l=1}^n a_k \overline{a_l} \langle e_k ,e_l\rangle \\ &= \sum_{k,l=1}^n a_k \overline{a_l} \delta_{kl} \\ &= \sum_{k=1}^n |a_k|^2\end{aligned}
となる( \delta_{kl} はクロネッカーのデルタ)。
証明終
なお,これは,n=\infty のときも同様のことが成立します。それは,パーセバルの等式 (Parseval’s equality) と呼ばれます。これに関しては,以下で解説しています。
より進んだ内容の記事
より進んだ内容を紹介しておきます。
基底から正規直交基底を作る
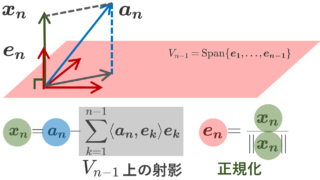
基底が一組あれば,そこから正規直交基底を作ることが可能です。グラムシュミットの直交化法 (Gram–Schmidt process) と呼ばれる手法を用います。以下で解説しています。
正規直交系が正規直交基底であるための条件
正規直交系が,正規直交基底であるための条件は,以下が知られています。
定理(正規直交系が正規直交基底である条件)
H をヒルベルト空間, \{e_\lambda\}_{\lambda \in \Lambda} \subset H を正規直交系とする。このとき,以下は同値である。
- \{e_\lambda\}_{\lambda \in \Lambda} は正規直交基底である
- \displaystyle x=\sum_{\lambda\in \Lambda} \langle x, e_\lambda\rangle e_\lambda ,\quad x\in H
- \displaystyle \| x\|^2=\sum_{\lambda\in \Lambda} |\langle x, e_\lambda \rangle |^2 (パーセバルの等式)
- \displaystyle \langle x,y\rangle =\sum_{\lambda\in \Lambda} \langle x, e_\lambda \rangle \overline{\langle y, e_\lambda \rangle} ,\quad x,y\in H
- \langle x, e_\lambda \rangle =0 \;(\lambda\in \Lambda)\implies x=0
本証明を完全に理解するには,以下の記事を順番に読んでいくとよいです。