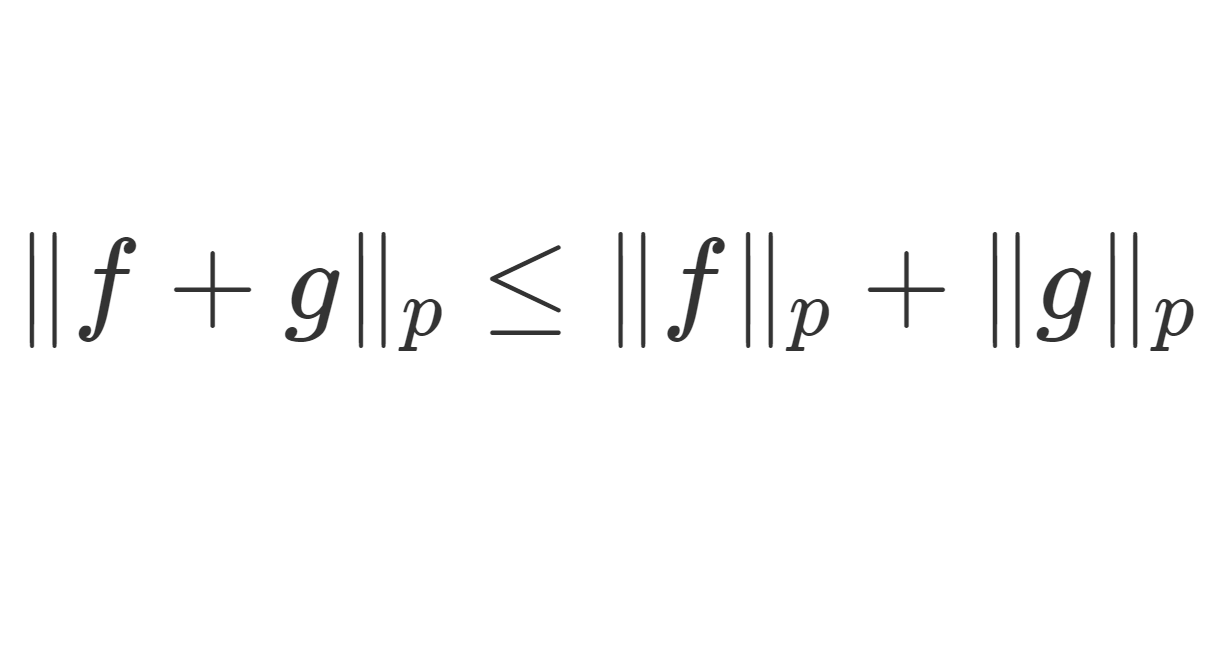ミンコフスキーの不等式とその証明

ミンコフスキーの不等式とは， $L^p$ ノルムに関する三角不等式

\|f+g\|_p\le \|f\|_p+\|g\|_p

のことをいいます。ミンコフスキーの不等式について，その証明を行いましょう。

ミンコフスキーの不等式
ミンコフスキーの不等式の証明
関連する記事

ミンコフスキーの不等式

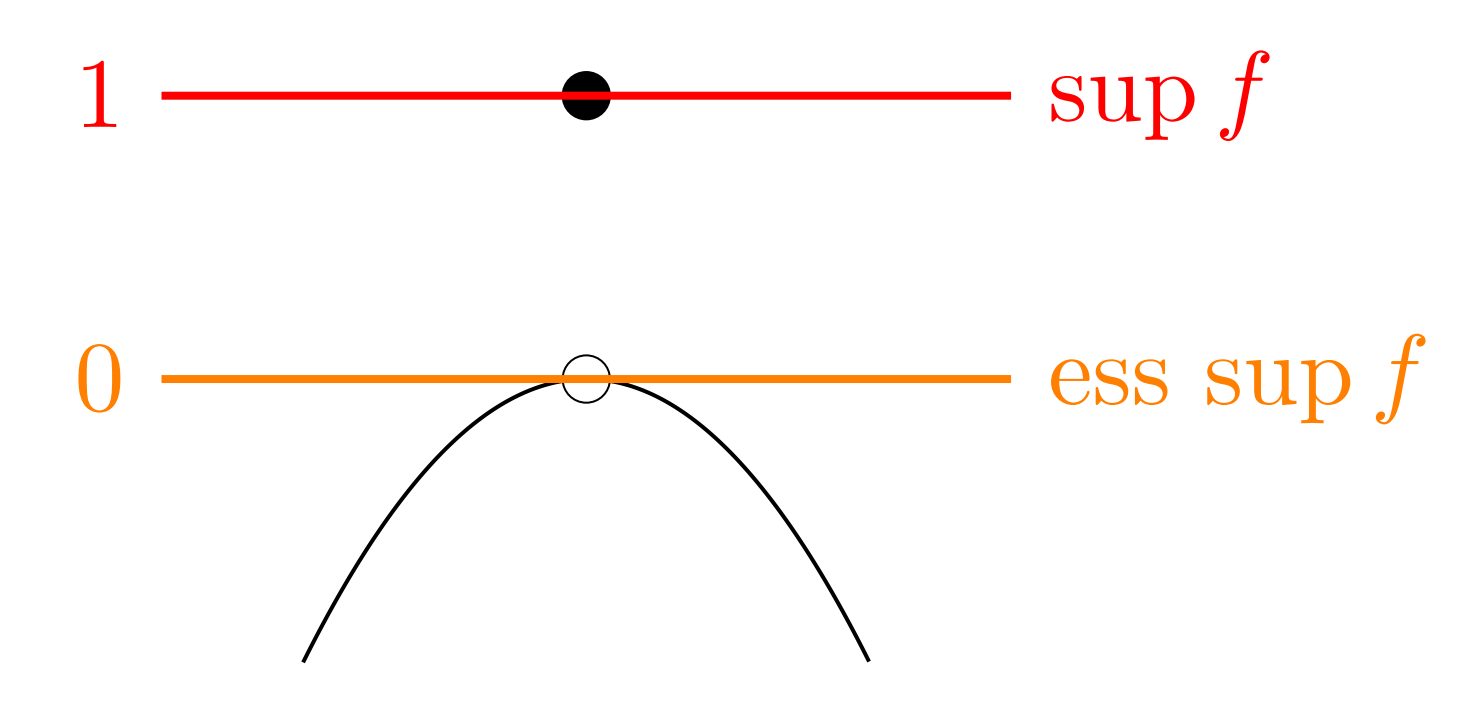
以下で， $1\le p<\infty$ のとき， $\|f \|_p=\left(\int_\R |f|^p\,dx\right)^{1/p}$ であり， $\|f\|_\infty = \inf\{ t\ge 0\colon \mu(|f|>t)=0\}$ ( $|f|$ の本質的上限; esssup， $\mu$ はルベーグ測度) とします。

また， $f\colon \R\to\R \, (\text{or } \mathbb{C})$ が $f\in L^p(\R)$ というのは， $\|f\|_p<\infty$ を意味します。 $L^p(\R)$ とは， $\|f\|_p<\infty$ となるような関数全体の集合です。

ミンコフスキーの不等式 (Minkowski’s inequality)

$1\le p\le \infty,\; f,g\in L^p(\R)$ とする。このとき，

\Large\color{red}\|f+g\|_p\le \|f\|_p+\|g\|_p

が成り立つ。特に， $f+g\in L^p(\R)$ である。

$1\le p<\infty$ のときは

\small \color{red}\!\! \left(\int_\R |f+g|^p\,dx\right)^{1/p}\!\!\! \le \!\left(\int_\R |f|^p\,dx\right)^{1/p}\!\!\!\!\!+\!\left(\int_\R |g|^p\,dx\right)^{1/p}

ですね。

ミンコフスキーの不等式は $L^p(\R)$ がノルム空間であるということを示しています。
実際， $f,g\in L^p(\R)\implies f+g\in L^p(\R)$ より $L^p(\R)$ はベクトル空間であり，また，ミンコフスキーの不等式そのものは，ノルムに関する三角不等式になっていますね。ノルムは，定義から三角不等式を必ず満たさねばなりませんから，これは $L^p(\R)$ がノルム空間であることの証明の一部になっています。

また，これはより一般の $L^p$ 空間でも成立します。すなわち， $1\le p<\infty$ のときは

\small \color{red} \!\! \left(\int|f+g|^p\,d\mu\right)^{1/p}\!\!\! \le \! \left(\int|f|^p\,d\mu\right)^{1/p}\!\!\!\!\!+\!\left(\int |g|^p\,d\mu\right)^{1/p}

が成り立ちます( $\mu$ はより一般の測度)。さらに，級数版のミンコフスキーの不等式

\small \color{red}\!\!\left(\sum_{n=1}^\infty |a_n+b_n|^p\right)^{1/p}\!\!\!\le\! \left(\sum_{n=1}^\infty |a_n|^p\right)^{1/p}\!\!\!\!\!+\!\left(\sum_{n=1}^\infty |b_n|^p\right)^{1/p}

も同様に成り立ちます。

ミンコフスキーの不等式の証明

$p=\infty$ のときは絶対値の三角不等式からほぼ明らかなので，それ以外の場合について $\|f+g\|_p\le \|f\|_p+\|g\|_p$ を証明しましょう。

証明

$1\le p<\infty$ のときに証明する。

簡単のため， $\alpha=\|f\|_p ,\; \beta=\|g\|_p$ と書くことにする。 $\alpha=0$ なら $f=0,\,\text{a.e.}$ であり，不等式は明らかである。同様に $\beta=0$ のときも明らかなので， $\alpha,\beta>0$ としてよい。

$\tilde{f}=f/\alpha,\; \tilde{g}=g/\beta$ とする。このとき， $\|\tilde{f}\|_p=\|\tilde{g}\|_p=1$ であることに注意する。

\begin{aligned} |f+g|^p&\le \bigl||f|+|g|\bigr|^p =(\alpha |\tilde{f}|+\beta|\tilde{g}|)^p\\ &= (\alpha+\beta)^p\!\left(\frac{\alpha}{\alpha+\beta}|\tilde{f}|+\frac{\beta}{\alpha+\beta}|\tilde{g}|\right)^p \\ &\le (\alpha+\beta)^p\!\left(\frac{\alpha}{\alpha+\beta}|\tilde{f}|^p+\frac{\beta}{\alpha+\beta}|\tilde{g}|^p\right)\end{aligned}

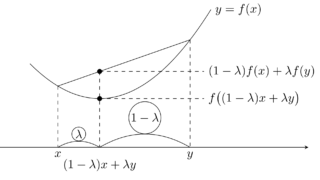
ただし，最後の不等式は関数 $x\mapsto x^p$ の凸性を用いた。両端辺を積分すると，

\begin{aligned}& \|f+g\|_p^p \\&\le (\alpha+\beta)^p\left(\frac{\alpha}{\alpha+\beta}\|\tilde{f}\|^p_p+\frac{\beta}{\alpha+\beta}\|\tilde{g}\|^p_p\right)\\ &=(\alpha+\beta)^p\left(\frac{\alpha}{\alpha+\beta}+\frac{\beta}{\alpha+\beta}\right)\\ &=(\alpha+\beta)^p\\ &= (\|f\|_p +\|g\|_p)^p \end{aligned}

であるから， $\|f+g\|_p\le \|f\|_p+\|g\|_p$ が成り立つ。

証明終

無事に証明できましたね。キーとなるのは $x\mapsto x^p$ の凸性でした。

$p=1$ のとき，等号成立はa.e.で $f,g$ が同符号になるときです。

また， $1<p<\infty$ のとき， $x\mapsto x^p$ は狭義凸なので，等号成立は $f=0,\,\text{a.e.}$ または $g=0,\,\text{a.e.}$ または $g=cf,\, \text{a.e.}$ となる定数 $c\ge 0$ が存在するとき( $\tilde{f}=\tilde{g},\,\text{a.e.}$ のとき)になります。

ミンコフスキーの不等式

ミンコフスキーの不等式の証明

関連する記事