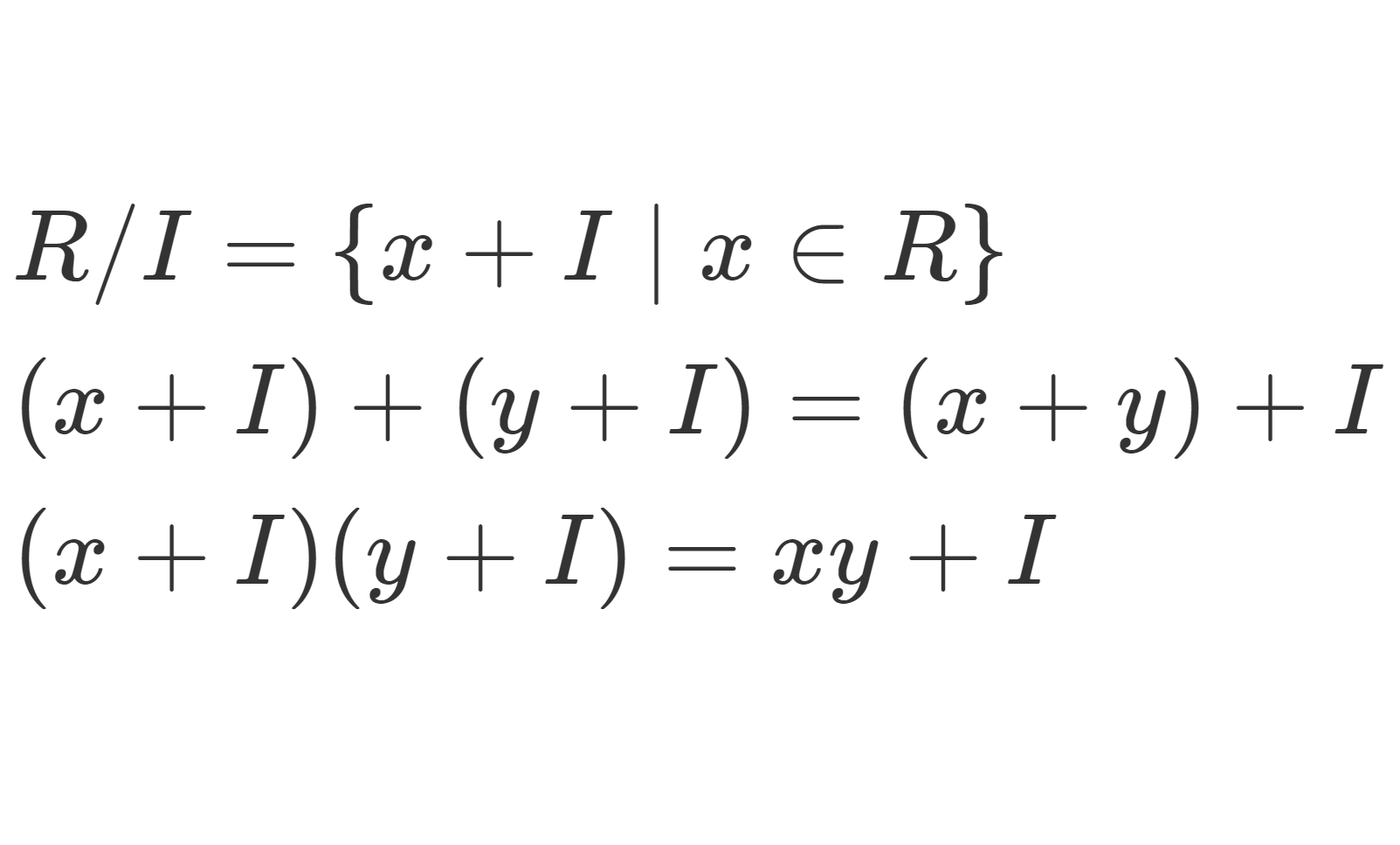剰余環,あるいは商環とは,両側イデアルによる同値類で割った商集合に入る環構造を指します。
剰余環を調べることは,環論において最も基本的なことの一つです。剰余環について,定義がwell-definedであることと,具体例を挙げましょう。
剰余環(商環)とは
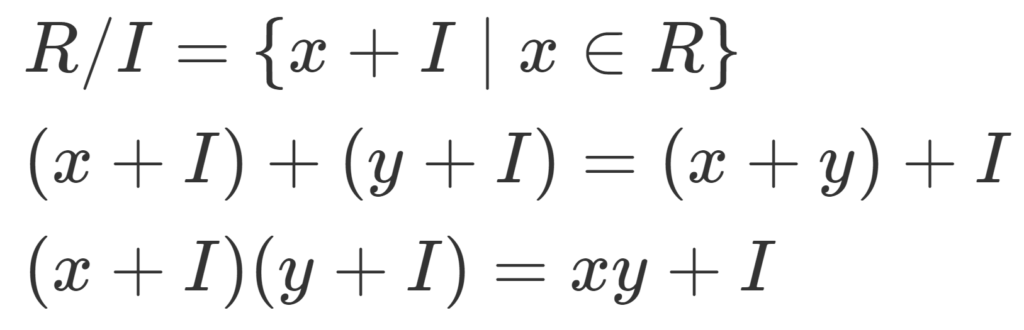
以下で,環と言えば単位的,すなわち乗法単位元 1 が存在し,零環(自明な環)でないとします。
剰余環(商環)の定義
定義(剰余環)
R を環, I\subset R を両側イデアルとする。このとき,剰余類の集合
R/I=\{ x+I\mid x\in R\}
は和と積の演算
によって環になる。これを剰余環 (factor ring) または商環 (quotient ring) という。
x+I とは x+I=\{ x+y\mid y\in I\} のことです。 R/I=\{ x+I\mid x\in R\} は x\sim y \iff x-y\in I による同値関係 \sim の商集合になっています。
I=\{0\} のときは R/\{0\}=R と解釈し, I=R のときは, R/R=\{0\} は零環(自明な環)と解釈します。
剰余類 R/I は環と見ることができることを確認しましょう。
剰余環(商環)が環であることの確認
まずは両側イデアルの復習をしておきましょう。
I\subset R が両側イデアル (two-sided ideal) であるとは,
- I は加法に関して部分群である
- x\in I, \, r\in R\implies rx\in I
- x\in I, \, r\in R\implies xr\in I
が成り立つことを言う。
R が可換環のときは,2,3.の区別はなく,両側イデアルは単にイデアルと呼ばれます。詳しくはイデアル(環論)とは~定義・具体例・基本的性質の証明~で解説しています。
R を和に関する群と見たときは,可換群ですから,部分群 I\subset R は常に正規部分群になります。よって,剰余群(商群)の議論により, R/I は和に関して群になることは分かります。ただ今回は,一応和に関して群になることも示しておきましょう。
示すべきは剰余群(商群)のときと同じで,演算が well-defined であることと,演算が環の定義をみたしていることです。
剰余環(商環)が環であることの証明
和がwell-definedであること
示すべきは x+I=x'+I, \,y+I=y'+I\implies (x+y)+I=(x'+y')+I である。
x-x'\in I,\, y-y'\in I であるから,
(x+y)-(x'+y')=(x-x')+(y-y')\in I.
これは, (x+y)+I=(x'+y')+I を意味する。
積がwell-definedであること
示すべきは x+I=x'+I, \,y+I=y'+I\implies xy+I=x'y'+I である。
x-x'\in I,\, y-y'\in I であることと, I が両側イデアルであるから,
xy-x'y'=x(y-y')-(x-x')y'\in I.
これは xy+I=x'y'+I を意味する。
和・積が環の定義をみたすこと
(x+I)+(y+I)=(x+y)+I ,\, (x+I)(y+I)= xy+I であるから,「R 上の演算 +I」という形をしている。よって R/I の演算規則は, R の演算規則を引き継ぐので,和・積は環の定義をみたす。
特に, R/I における加法単位元は I で,乗法単位元は 1+I である。
証明終
証明からもわかるように, R が可換環ならば R/I も可換環です。
なお, x+I=x'+I であることを,\color{red} x\equiv x'\pmod I と書くこともあります。
剰余環(商環)の例
例1.
m\ge 2 を整数とする。
可換環 \mathbb{Z} に対し,m\mathbb{Z}\subset\mathbb{Z} はイデアルである。よって,\mathbb{Z}/m\mathbb{Z} は剰余環である。
\mathbb{Z}/m\mathbb{Z} の元は, x+m\mathbb{Z} の形です。m の倍数で区別しないということですね。 x+m\mathbb{Z} を \overline{x} と略記すると,
\mathbb{Z}/m\mathbb{Z} =\{\overline{0},\overline{1},\dots, \overline{m-1}\}
であり, \overline{a},\overline{b}\in \mathbb{Z}/m\mathbb{Z} に対し,和と積の演算は
となっています。これは{}\bmod m の世界ですね。 \overline{a}=\overline{b} のことを, a\equiv b\pmod m と書くこともあります。
例2.
\mathbb{R}[x] を 実数係数1変数多項式環とすると, \mathbb{R}[x]/(x) は剰余環であり, \mathbb{R}[x]/(x)\simeq \mathbb{R} である。
(x) は x で生成されるイデアルです(→イデアル(環論)とは~定義・具体例・基本的性質の証明~)。
\mathbb{R}[x]/(x) の元は a+x\mathbb{R}[x] の形です。特に,多項式の1次以上の部分で区別せず, a+x\mathbb{R}[x]\in \mathbb{R}[x]/(x) と a\in\mathbb{R} を環として同一視することができます。
ゆえに,環として \mathbb{R}[x]/(x)\simeq \mathbb{R} (同型)です。この辺は,詳しくは準同型定理の話です(その際の準同型写像は f(x)\mapsto f(0))。
例3.
\mathbb{R}[x]/(x^2+1)\simeq \mathbb{C} である。
剰余環 \mathbb{R}[x]/(x^2+1) と複素数 \mathbb{C} は写像 f(x)\mapsto f(\sqrt{-1}) により同一視可能です。これも準同型定理の話です。
自然な射影(準同型)
\large \color{red}\pi \colon R\ni a \mapsto a+I \in R/I
は自然な環準同型写像になります。これを,自然な射影といいます。このとき,\pi は全射で, \operatorname{Ker}\pi =I です。
定義は覚えておきましょう。