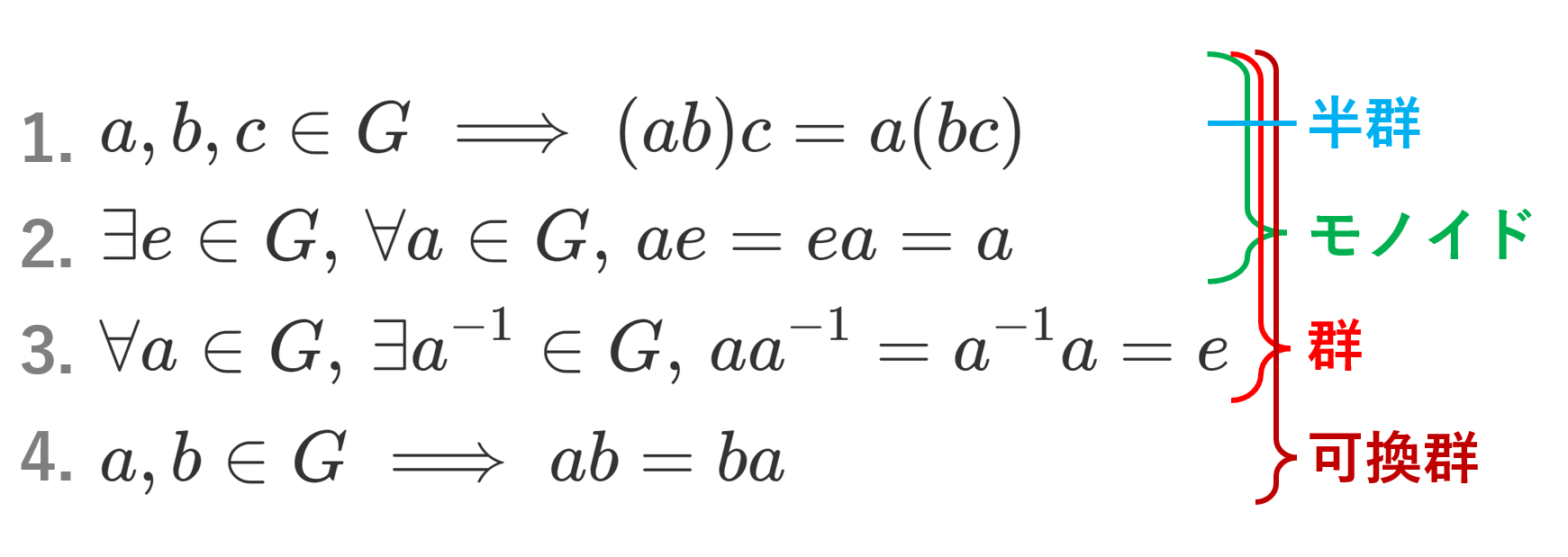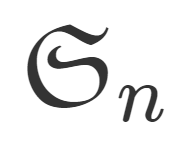群・可換群(アーベル群・加法群)とは,一般の集合の上に,いい感じの二項演算を定めた集合です。抽象代数学の入り口と言っていいでしょう。
これについて,その定義と具体例を,ていねいに述べましょう。最後には群の基本的な性質も述べます。
群の定義・可換群(アーベル群)の定義
群を考える最大のメリットは,「定義が抽象的なため,さまざまな演算を統一的に扱える」ことです。定義を確認しましょう。
定義(群・可換群(アーベル群))
集合 G 上に二項演算 G\times G \ni (a,b)\mapsto ab \in G が定義されていて,
- (ab)c = a(bc) (結合法則)
- 「任意の a\in G に対し, ae = ea = a 」となる元 e\in G が存在する(これを単位元・単元 (unit) という)
- 任意の a\in G に対し,「 aa^{-1}=a^{-1}a=e となる元 a^{-1}\in G が存在」する(これを a の逆元 (inverse) という)
のうち,1.をみたすとき半群 (semigroup),1,2.をみたすときモノイド (monoid),1,2,3.の全てをみたすとき群 (group) という。また,上に加えて,
4. 任意の a,b \in G に対して, ab=ba
が成立するとき,可換群 (commutative group) またはアーベル群 (Abelian group),加法群 (additive group) という。
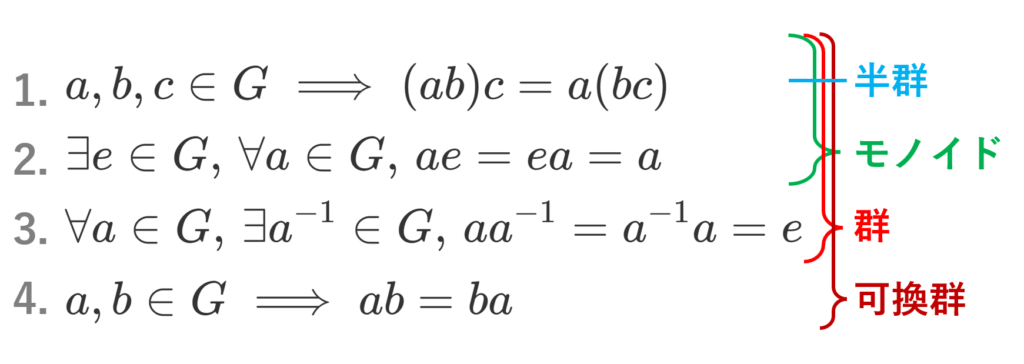
二項演算とは,集合 G 上に定まっている写像 G\times G\ni (a,b)\mapsto \phi(a,b)\in G を指します。今回は,この写像を便宜上 \phi(a,b)=ab と書いているわけですね。
群における二項演算は積 (product) と呼ばれることが多いです。 ab の代わりに, a\cdot b とかくこともあります。また (ab)c=a(bc) ですから,この両者を区別する必要がなく,単に abc とかくのが普通です。
単位元は e と書きましたが, 1 と書くこともあります。
可換群(アーベル群・加法群)における二項演算は,積の代わりに和 (sum) と呼び, a+b のように書くことも多いです。
群・可換群(アーベル群)の具体例6つ
難しい概念は具体例を通して理解するのが一番です。早速,具体例を挙げましょう。
- 群である例
- 群でない例
の両方を述べます。
群・可換群(アーベル群)である例
例1( 0 でない実数の積).
G= \mathbb{R}\setminus \{0\} は通常の積の演算(かけ算)に関して群をなす。実際,
- a,b,c\in G \implies (ab)c=a(bc)
- 1 は任意の a\in G に対して a1=1a = a が成立する単位元である。
- a\in G に対し, 1/a\in G は a (1/a)= (1/a)a=1 をみたす逆元である。
また, ab=ba も成り立つので,可換群(アーベル群・加法群)である。
G=\mathbb{R}\setminus \{0\} は二項演算を「かけ算」と思うことで群ですね。 \mathbb{R} から 0 を除いているのは, 0 にはかけ算して 1 になる逆元がないからです。
なお,\mathbb{Q}\setminus \{0\} や,\mathbb{C}\setminus\{0\} も,通常の積に関して群になります。その証明は,例1.と全く同じです。
例2(実数の和).
\mathbb{R} は通常の和の演算(足し算)に関して群をなす。実際,
- a,b,c\in \mathbb{R} \implies (a+b)+c = a+(b+c)
- 0 は任意の a\in \mathbb{R} に対して a+0 = 0+a=a が成立する単位元である。
- a\in \mathbb{R} に対し, -a\in \mathbb{R} は a+(-a)=(-a)+a=0 をみたす逆元である。
また, a+b=b+a も成り立つので,可換群(アーベル群・加法群)である。
「和」という二項演算 \mathbb{R}\times \mathbb{R}\ni (a,b) \mapsto a+b\in \mathbb{R} を考えても,これは群をなしますね。
例1.のように,積について群と思ったときの単位元・逆元はそれぞれ 1, 1/a でしたが,今回にように,和について群と思ったときの単位元・逆元はそれぞれ 0, -a になります。
なお, \mathbb{Z},\mathbb{Q},\mathbb{C} も,和に関して群になります。
もう少しレベルを上げましょう。
例3(行列群).
n 次正則行列(可逆行列)全体の集合
\!\!\! \mathrm{GL}_n(\mathbb{R})\! = \! \{ A\!=\!(a_{ij})_{1\le i,j\le n} \mid a_{ij}\in\mathbb{R}, \det A \!\ne\! 0\}
は行列の積に関して群をなす。実際,
- A,B,C\in \mathrm{GL}_n(\mathbb{R}) \implies (AB)C=A(BC)
- 単位行列 I\in \mathrm{GL}_n(\mathbb{R}) は,任意の A\in \mathrm{GL}_n(\mathbb{R}) に対して, AI=IA=A が成立する単位元である。
- 逆行列 A^{-1}\in \mathrm{GL}_n(\mathbb{R}) は, AA^{-1}=A^{-1}A= I が成立する逆元である。
一般に, AB\ne BA なので,可換群(アーベル群・加法群)ではない。この群を一般線形群ということもある。
可逆行列の演算は,群であるが可換群(アーベル群)でない典型的な例ですね。
例4(対称群).
全単射 \sigma \colon \{ 1,2,\dots, n\} \to \{1,2,\dots, n\} を置換という。置換全体の集合 S_n は写像の合成に関して群をなす。実際,
- \sigma, \tau, \eta \in S_n \implies (\eta\circ \tau)\circ \sigma = \eta\circ (\tau\circ \sigma)
- 恒等写像 \operatorname{id} は \sigma \circ \operatorname{id}=\operatorname{id}\circ \sigma =\sigma をみたす単位元である。
- \sigma \in S_n に対し, \sigma^{-1}\in S_n は \sigma\circ \sigma^{-1}=\sigma^{-1}\circ \sigma =\operatorname{id} をみたす逆元である。
この群を対称群 (symmetric group) という。一般に \tau \circ \sigma\ne \sigma \circ \tau なので,これは可換群(アーベル群・加法群)でない。
このように,定義域・終域が同じ全単射の集合も「合成」という演算 \tau\circ \sigma \in S_n によって,群をなします。
記法については,いちいち写像の合成の記号 \circ をかいて \tau \circ \sigma とするのは面倒なので,単に \tau \sigma のように書くことが多いです。
対称群については,以下で詳しく解説しています。
このように,さまざまな演算を統一的に扱えるのが「群」なわけです。数学で群を考えるメリットはここにあります。
群でない例
群でない例も理解しておきましょう。
例5.
A= \mathbb{Z}\setminus \{0\} は,通常の積に関するモノイドであるが群でない。実際,
- a,b,c\in A \implies (ab)c=a(bc)
- 1 は単位元
であるが,逆元がない。
A= \mathbb{Z}\setminus \{0\} にはかけ算して 1 になるような逆元がありません。たとえば, 2 \in A には 1/2 が逆元になり得ますが,これは A 内の集合でありませんね。
例6.
自然数の集合 \mathbb{N}=\{1,2,3,\dots\} は,通常の和に関する半群であるが,モノイドや群でない。実際,
- a,b,c \in\mathbb{N} について (a+b)+c=a+(b+c)
が成立するが, \mathbb{N} 内に単位元 0 はないし,逆元 -a もない。
群の基本的な性質~群の単位元・逆元の一意性と計算~
群の定義の根幹にかかわる,基本的な性質を紹介し,証明しておきましょう。
定理(群の単位元・逆元の一意性と計算)
G を群とする。このとき,
- 単位元 e は一意である。
- a\in G に対して,その逆元 a^{-1} は一意である。
- a,b\in G に対して, (ab)^{-1} = b^{-1}a^{-1}.
- a\in G に対して, (a^{-1})^{-1} = a.
- a,b\in G に対して,
- ab = e\implies b=a^{-1}.
- ba= e\implies b=a^{-1}.
5.は, ab=ba=e ではなく, ab=e のように1等式しか言えていなくても,逆元であることが分かってしまうと言っています。
順番に証明していきましょう。
証明
1. の単位元の一意性について
e, e' \in G を共に単位元とすると,単位元の定義より,
e=ee' = e'.
2. の逆元の一意性について
b,b' を共に a の逆元とすると,逆元の定義より,
b = b(ab') =(ba)b' = b' .
3. (ab)^{-1} = b^{-1}a^{-1} について
より,逆元の定義から, (ab)^{-1} = b^{-1}a^{-1}.
4. (a^{-1})^{-1} =a について
逆元の定義式, aa^{-1} = a^{-1}a = e は, a^{-1} の逆元が a であることも示している。よって, (a^{-1})^{-1}=a である。
5. ab = e\implies b=a^{-1},\, ba=e\implies b=a^{-1} について
ab=e の両辺左から a^{-1} をかけて b=a^{-1} がわかり, ba=e の両辺右から a^{-1} をかけて b=a^{-1} がわかる。
証明終
1.の証明は単位元の定義しか使っていませんし,2.の証明は逆元の定義しか使っていません。よって,群でなくても,「単位元が存在すれば一意」や「逆元が存在すれば一意」であることは言えます。
たとえば,モノイドにおいても,単位元は一意です。