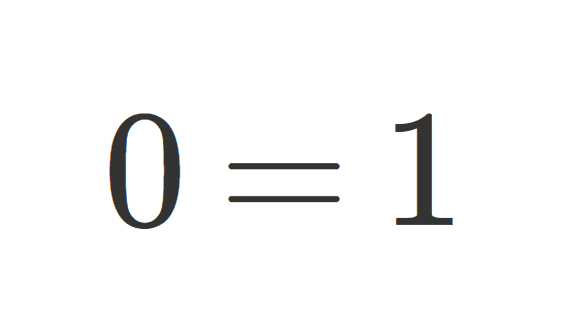零環(自明な環)とは,たった一つの元しか持たない環のことを言います。これについて,その定義と,零環(自明な環)が 0=1 をみたす唯一の環であることの証明をしましょう。
零環(自明な環)とは
定義(零環)
R=\{0\} に対し,和と積の演算
\color{red} \begin{aligned}0+0&=0,\\ 0\times 0 &=0\end{aligned}
を定めると,これは環の定義をみたす。これを零環 (the zero ring) または自明な環 (trivial ring) という。
0 しか元がない非常に単純な環のことですね。
零環は0=1をみたす唯一の環
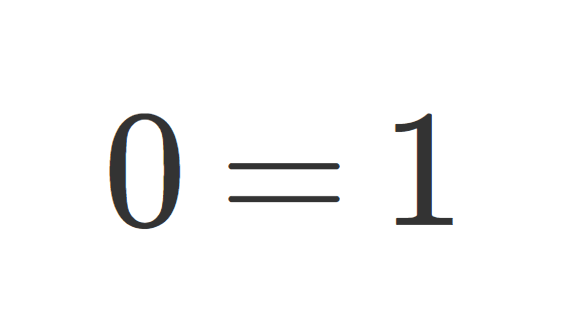
0=1 というとトンデモっぽいですが,ここでいう 0 は加法の単位元で, 1 は乗法の単位元を指します。
定理(零環は 0=1 をみたす唯一の環)
R を環とし,加法単位元 0 と乗法単位元 1 が一致しているとする。このとき, R は零環である。