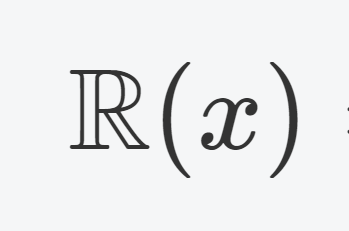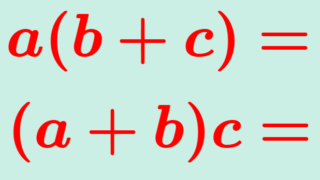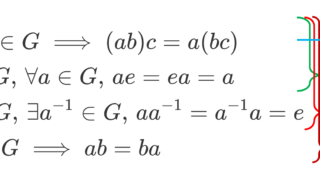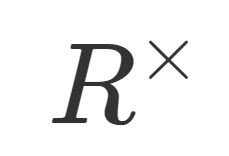体の定義と具体例4つ

数学，とくに代数学における体 (field) とは，四則演算が定義された集合のことを言います。一般に，代数学においては，

群はかけ算・わり算が定義された集合
環は足し算・引き算・かけ算が定義された集合
体は足し算・引き算・かけ算・わり算（四則演算）が定義された集合

をいいます。本記事では環の定義を前提に，体の定義と具体例を述べましょう。

体の定義
体の具体例4つ
体の性質
関連する記事

体の定義

体というのは，ざっくりいうと四則演算が定義された集合のことを言います。厳密に定義を述べると，以下のようになります。

定義（体）

空でない集合 $K$ が体 (field) であるとは，

$K$ が単位元を持つ可換環
$K$ の $0$ でない任意の元が乗法逆元を持つ，すなわち， $a\ne 0$ に対し， $aa^{-1}=1$ となるものが存在する。言い換えると $K^\times = K\setminus\{0\}$ である

の2つが成り立つことをいう。ただし， $K^\times$ とは $K$ の乗法群を指す。

1.の可換環とは，足し算・引き算・かけ算が定義されている集合です。「可換」とはかけ算について $ab=ba$ と入れ替え可能なことを意味しています。それに加え，2.で割り算もできると言っているわけです。

念のため，1.で出てくる環の定義を述べておきましょう。

環・可換環の定義

$(R,+)$ は可換群(アーベル群)である。すなわち，
a. ${(a+b)+c=a+(b+c)}$ (結合法則)
b. ${a+0=0+a=0}$ (加法単位元 $0$ の存在)
c. ${a+(-a)=(-a)+a=0}$ (加法逆元 $-a$ の存在)
d. ${a+b=b+a}$ (可換性)
$(R,\times)$ はモノイドである。すなわち，
a. ${(ab)c=a(bc)}$ (結合法則)
b. ${1a=a1=a}$ (乗法単位元 $1$ の存在)
$+,\times$ の間の分配法則，すなわち，
a. ${ a(b+c)=ab+ac}$
b. ${ (a+b)c=ac+bc}$

が成り立つとき，環 (ring) という。

さらに乗法について $ab=ba$ (可換性)が成り立つとき，可換環 (commutative ring) という。

詳しくは環の定義・可換環の定義とその具体例6つで解説しています。

なお，体に可換性を課さないこともあります。1.で，可換環でなく単なる環に変えたものを特に斜体 (skew field) といい，可換なときはそれを強調して可換体 (commutative field) ということもあります。逆に非可換なときは非可換体 (non-commutative field) ということもあります。

本記事では，単に「体」というと上の定義で述べた通り可換体を指すことにします。

また，位数(すなわち集合としての元の個数)が有限な体を有限体 (finite field) といいます。

体の具体例4つ

例1(数の集合).

$\mathbb{Q,R,C}$ は体である。 $\mathbb{Z}$ は可換環であるが体ではない。

有理数 $\mathbb{Q}$ ，実数 $\R$ ，複素数 $\mathbb{C}$ はそれぞれ四則演算ができますから，体です。一方で，一般に整数 $\mathbb{Z}$ は乗法逆元が $\mathbb{Z}$ 内に存在しませんから，体ではないです。ただかけ算は出来るので，環ではあります。

例2(有限体)

$p$ を素数とするとき， $\mathbb{Z}/p\mathbb{Z}$ は体である。

${}\bmod{p}$ の世界ですね。 $p$ が素数のときは，任意の $a$ に対して， $aa^{-1}\equiv 1\pmod p$ となる $a^{-1}$ が存在しますから，体です。

なお $p$ が素数でないと，これは成り立ちません。たとえば， ${}\bmod{4}$ の世界 $\mathbb{Z}/4\mathbb{Z}$ を考えると， $2m\equiv 1\pmod 4$ となる $m$ は存在しないです( $m\equiv 0,1,2,3$ を順に代入すれば確認できます)。よって， $\mathbb{Z}/4\mathbb{Z}$ は可換環だが体ではないです。

例3(有理関数体)

$f(x), g(x)$ を多項式とし， $g(x)\ne 0$ とする。このとき， $f(x)/g(x)$ の形の式を有理関数 (rational function; 有理式) という。有理関数全体の集合は体になる。記号でかけば，