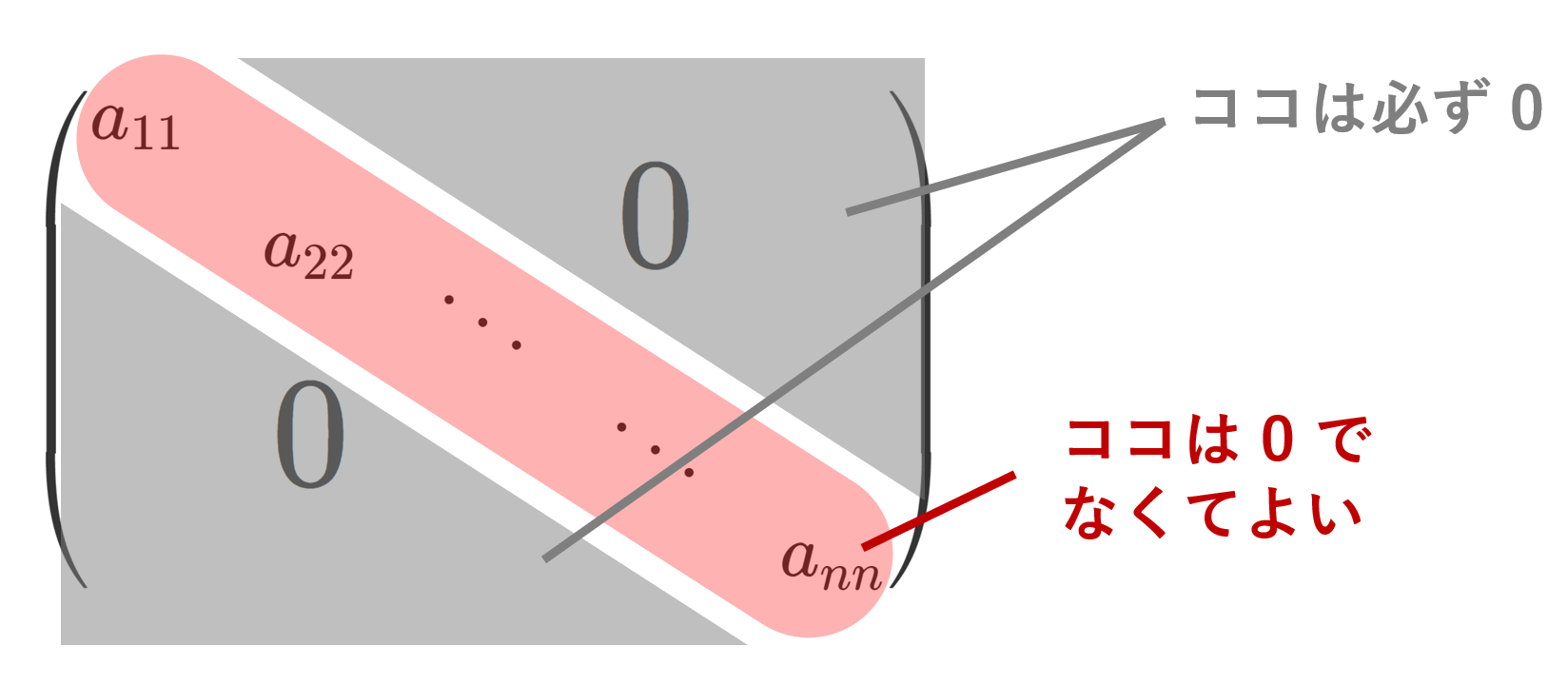
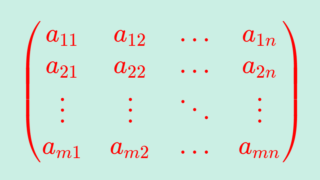正方行列において,(左上から右下への)対角成分以外が0となる行列
\begin{pmatrix} a_{11} \\ & a_{22} && \huge{0} \\ & & \ddots \\ &\huge{0}&& \ddots \\ &&&& a_{nn} \end{pmatrix}
を対角行列といいます。これの定義と性質を確認しましょう。
対角行列の定義
もう一度,正確な定義を述べることにします。
定義(対角行列)
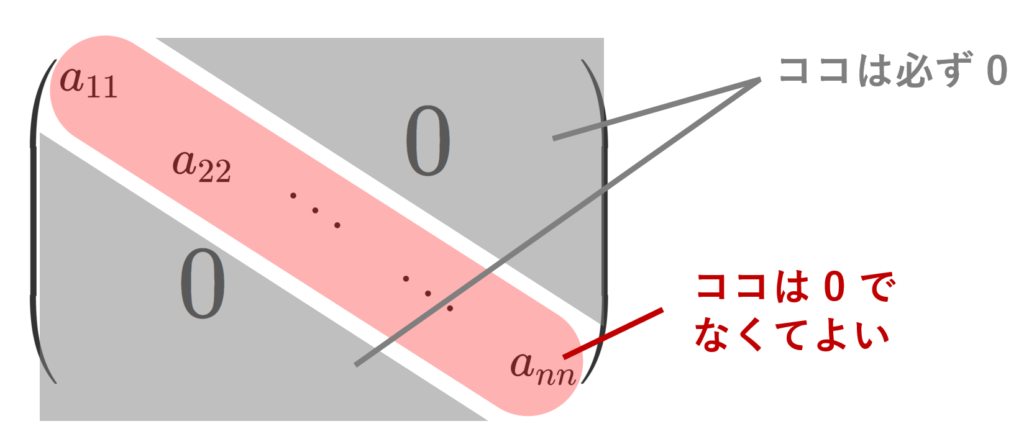
A = (a_{ij}) を n 次正方行列とする。
\color{red}i\neq j \implies a_{ij} = 0
となるとき,すなわち,
のとき, A を対角行列 (diagonal matrix) という。
対角行列は,\color{red} \operatorname{diag} (a_{11}, a_{22}, \dots , a_{nn} ) のような書き方をすることもあります。
なお一般の行列に対し,, a_{11}, a_{22}, \dots , a_{nn} のことを対角成分と言います。
対角行列の具体例
少しだけ具体例を挙げましょう。
対角行列の具体例
- \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{pmatrix} は対角行列
- \begin{pmatrix} 0 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 7 \end{pmatrix} は対角行列
- 零行列や単位行列は対角行列
対角成分以外は,必ずゼロでないといけませんが,対角成分にもゼロがあって構いません。
対角行列の基本的な性質6つ
定理(対角行列の性質)
A =(a_{ij}), B=(b_{ij}) を n 次の対角行列とする。このとき,
- 対角行列の和・定数倍はまた対角行列である。
- AB = BA= \begin{pmatrix}
a_{11} b_{11} \\
& a_{22}b_{22} && \huge{0} \\
& & \ddots \\
&\huge{0}&& \ddots \\
&&&& a_{nn}b_{nn}\end{pmatrix} .
特に,対角行列の積もまた対角行列である。 - A^\top = A. (転置行列)
特に,対角行列は対称行列である。 - \det A = a_{11}a_{22} \dots a_{nn}. (行列式)
- a_{ii}\neq 0 \,\, (1\le i\le n) のとき,
A^{-1}= \begin{pmatrix} a_{11}^{-1} \\ & a_{22}^{-1} && \huge{0} \\ & & \ddots \\ &\huge{0}&& \ddots \\ &&&& a_{nn}^{-1}\end{pmatrix}.
特に,逆行列もまた対角行列である。 - A の固有値は a_{11}, a_{22}, \dots , a_{nn} となる。
証明は簡単なので省略します。