ベルンシュタインの定理とは,2つの集合それぞれを定義域・終域とする双方向の単射があれば,全単射があるという定理です。ベルンシュタインの定理について,イメージ図を交えて証明していきましょう。
ベルンシュタインの定理とその証明
ベルンシュタインの定理(Schröder–Bernstein theorem)
A,B を空でない集合とする。単射 f\colon A\to B と単射 g\colon B\to A が存在するならば,全単射 F\colon A\to B が存在する。
言い換えれば, A,B の間に双方向の単射がそれぞれ存在すれば, A と B の濃度は等しい,ということになります。全単射の存在が示せなくても,濃度が等しいといえる定理なんですね。
証明しましょう。
証明
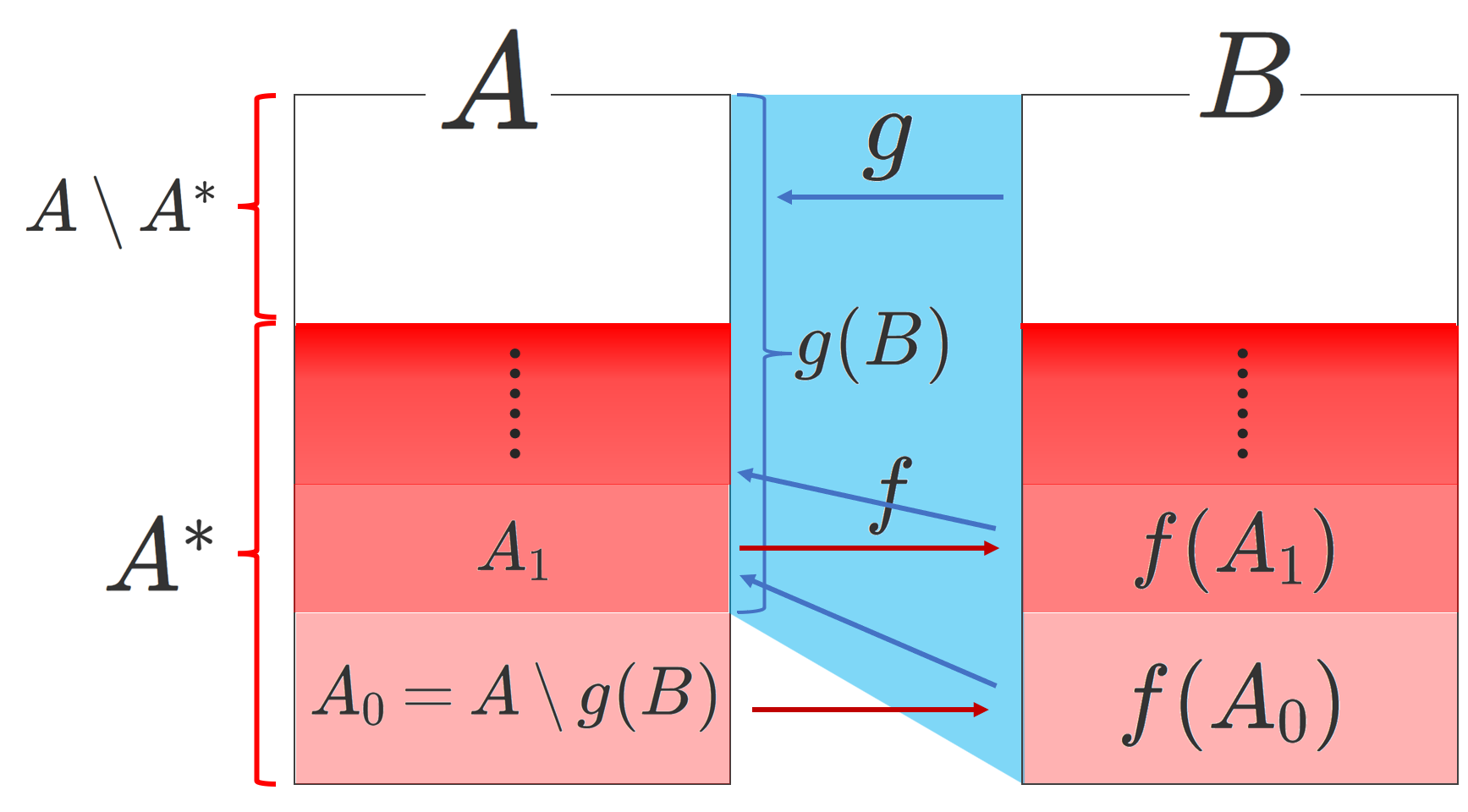
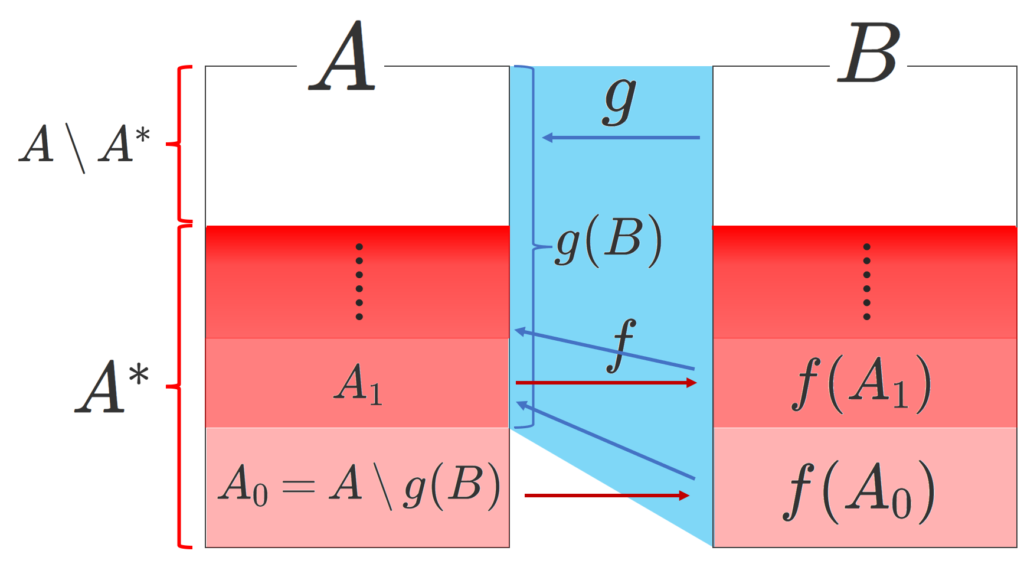
A_0=A\setminus g(B) とし,以下 A_n = g(f(A_{n-1})) \; (n=1,2,\dots) と定める。 A^*=\bigcup_{n=0}^\infty A_n とし,
F(x)= \begin{cases} f(x) & x\in A^*, \\ g^{-1} (x) & x\in A\setminus A^* \end{cases}
と定めると, F\colon A\to B は全単射になることを示そう。
まず, A\setminus A^*\subset A\setminus A_0=g(B) であるから, x\in A\setminus A^* に対して, g^{-1}(x)\in B はただ一つ定まるため, F は写像としてwell-definedである。
\begin{aligned}F(A\setminus A^*)&=g^{-1}(A\setminus A^*) \\ &= g^{-1}(A)\setminus g^{-1}(A^*)\\&=B\setminus g^{-1}(A^*),\\ g^{-1}(A^*)&= \bigcup_{n=0}^\infty g^{-1}(A_n) \\ &=\bigcup_{n=1}^\infty g^{-1}( g(f(A_{n-1}))) \\ &= \bigcup_{n=1}^\infty f(A_{n-1}) = f(A^*) \end{aligned}
である。ただし,下から2行目の = は g^{-1}(A_0)=\emptyset を用いた。これより,
であり,これは F が全射であることを示している。
F の単射性について, f, g^{-1}|_{A\setminus A^*} はともに単射であるから, x\in A^*,\, y\in A\setminus A^* として, F(x)\ne F(y) すなわち f(x)\ne g^{-1}(y) を示せばよい。
f(x)=g^{-1}(y) と仮定する。 x\in A_n とすると, g(f(x))=y より, y\in A_{n+1}\subset A^* となって矛盾する。よって f(x)\ne g^{-1}(y) であり, F は単射である。
証明終