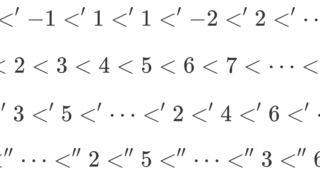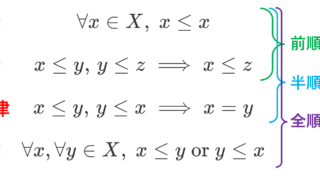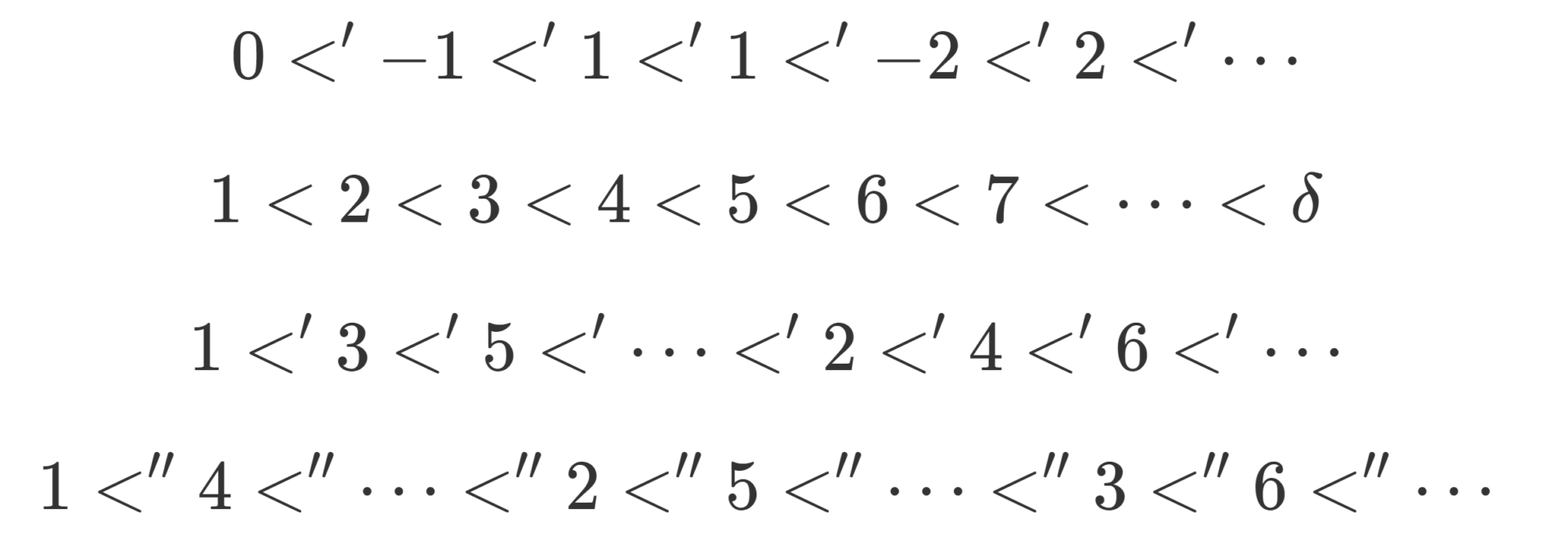超限帰納法とは,数学的帰納法の議論をより一般の整列集合に適用したものです。超限帰納法について,その内容を紹介しましょう。
超限帰納法
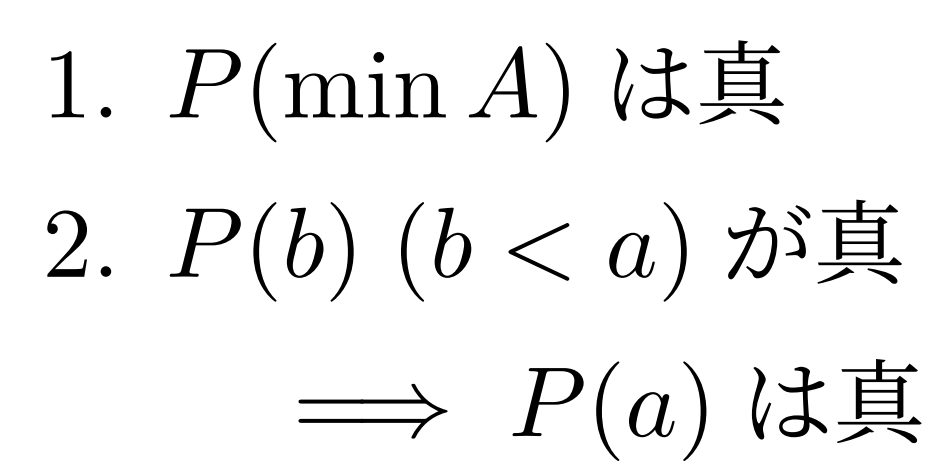
超限帰納法の準備~整列集合~
超限帰納法を理解するには,整列集合の理解が必要です。整列集合について述べておきましょう。
全順序集合のうち,任意の空でない部分集合が最小元をもつものを整列集合 (well-ordered set) という。
たとえば,\mathbb{N}=\{1,2,3,\dots\} は整列集合ですが,閉区間 [0,1] は通常の大小関係に関して整列集合ではありません。
また,\mathbb{N} に奇数・偶数同士なら通常の大小を採用し, x が奇数, y が偶数なら x<y とした順序集合
1<3<5<7<\dots < 2<4<6<8<\dotsも整列集合です。このような整列集合にも使える帰納法が,超限帰納法です。
超限帰納法とは
超限帰納法 (transfinite induction)
A を整列集合とし,各 a\in A に対し,命題 P(a) が与えられているとする。もし,
- P(\min A) が真であること
- b<a をみたす全ての b\in A に対し, P(b) が真であるとき, P(a) も真になること
の2つが成り立てば,全ての a\in A で P(a) は真である。
証明
真でない集合 A_1= \{a\in A\mid P(a) \text{ is false}\} とおく。 A は整列集合より, A_1\ne \emptyset なら最小値 a_1\in A_1 が存在する。
a_1 の定義から,各 b<a_1 に対し P(b) は真である。よって,2.より P(a_1) も真となり, a_1\in A_1 に矛盾する。よって A_1=\emptyset となって証明が終わる。
証明終
超限帰納法を整列集合 \mathbb{N} に適用したものが数学的帰納法です。ただし,\mathbb{N} が整列集合であるということは,ペアノの公理からくる話で,難しいです。
余談ですが,超限帰納法を「超元気農法」と誤変換してしまうのは,数学科あるあるですよね。