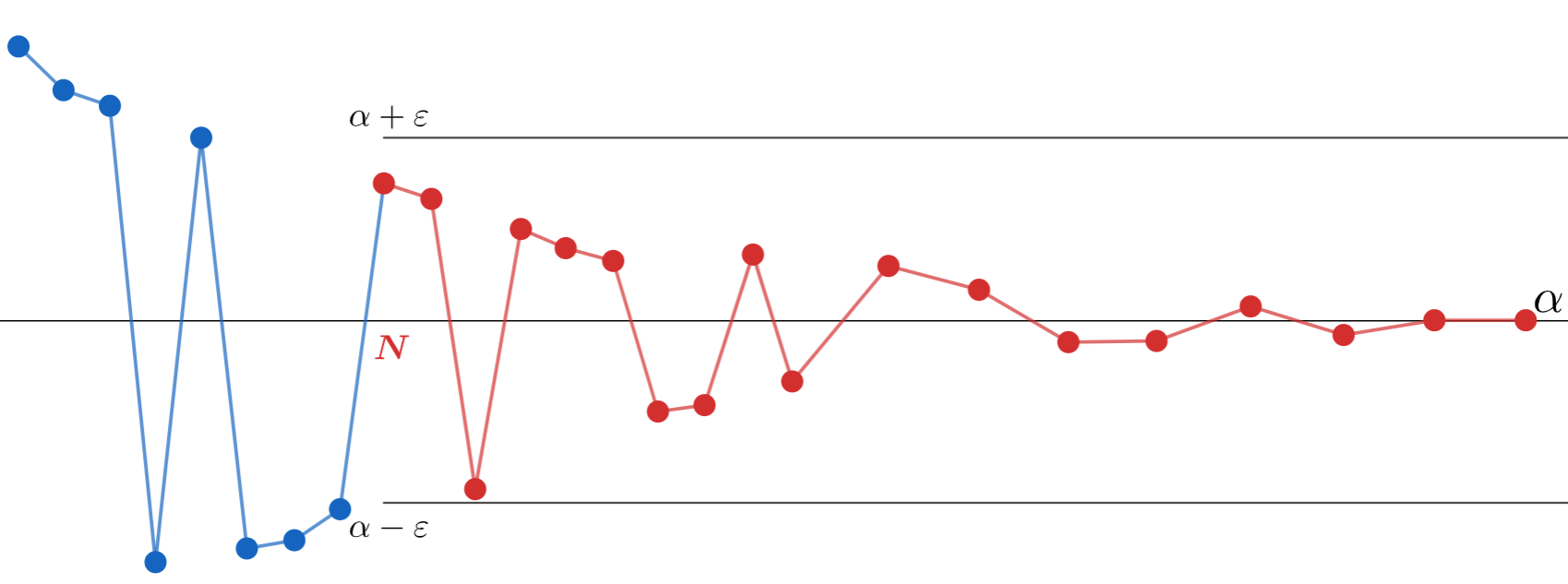
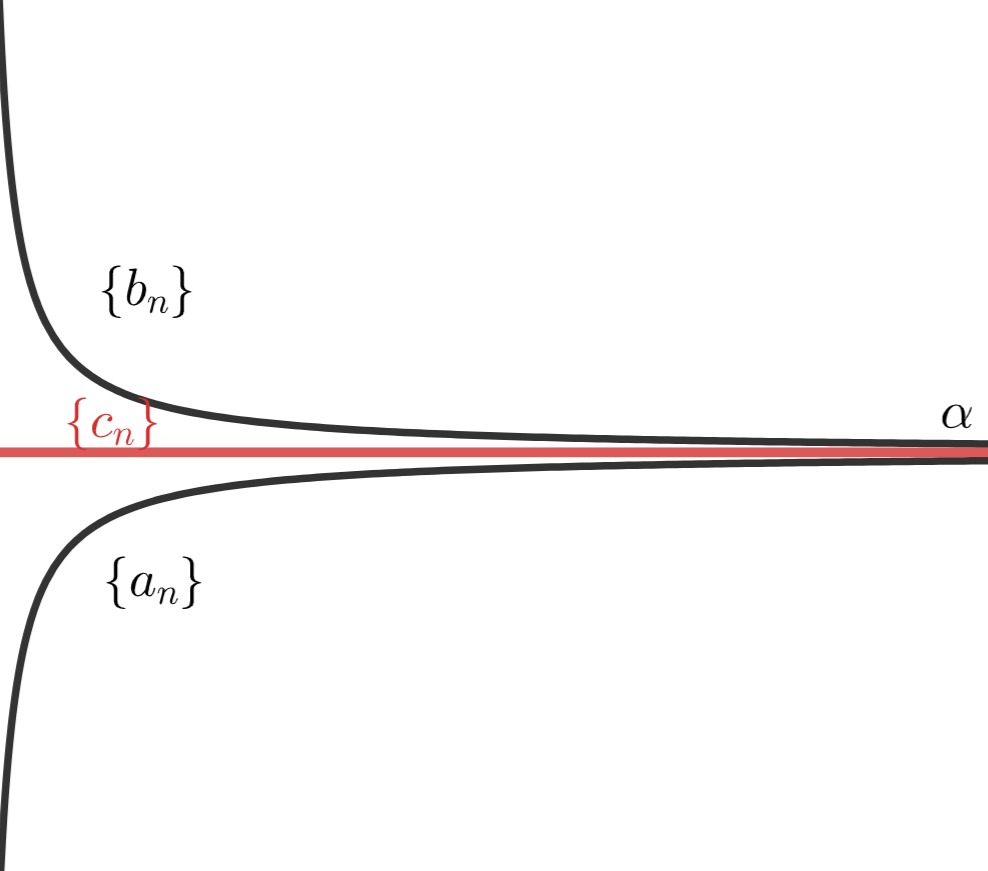
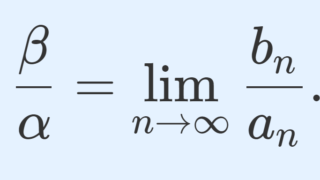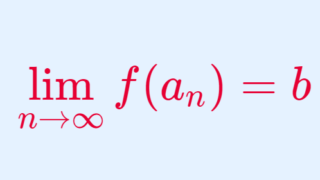大学数学の微分積分学での最初の関門といえば,主に数列の極限を定義する \varepsilon\text{-}N 論法や,主に関数の極限を定義する \varepsilon\text{-}\delta 論法でしょう。今回はそのうちの \varepsilon\text{-}\delta 論法について時間をかけて解説していきます。ゆっくりと読み進めていきましょう。
ε-δ論法~関数の極限と連続の定義~
まずは \varepsilon\text{-}\delta 論法による定義を2つ確認しましょう。
関数の極限の定義
関数の定義域は,簡単のため \mathbb{R} とすることにしましょう。実際には a の近くで定義されていれば問題ありません。
定義(関数の極限)
f\colon \mathbb{R} \to \mathbb{R}, \, a\in \mathbb{R} とする。このとき,
\lim_{x\to a} f(x) = b, \quad f(x) \longrightarrow b \,\, (x\to a)
または f(x) が x \to a のとき b に収束する (converge) とは,
任意の \boldsymbol{\varepsilon > 0} に対して,ある \boldsymbol{ \delta > 0} が存在して,
\boldsymbol{0 < | x - a| < \delta \implies |f(x) - b| < \varepsilon}
が成立することをいう。このときの b を x\to a としたときの f の極限 (limit) または極限値 (limit value) という。
なお,この定義は∀(全称記号,任意の)と∃(存在記号,存在する)の使い方を知っているのであれば,
\color{red}\begin{aligned}&\forall \varepsilon>0 ,\exists \delta>0, \\ &0<|x-a|<\delta\implies |f(x)-b|<\varepsilon \end{aligned}
とかけます(本記事では知らなくても読めます)。
とにかく難しいと思います。 \varepsilon\text{-} N 論法と同様に,すぐに理解できる人はなかなかいないでしょう。数学者でも,最初は難しいと思ったに違いありません。自分もかなり苦戦しました。徐々に慣れていきましょう。
なお, 0 < | x - a| < \delta \implies |f(x) - b| < \varepsilon のところの \boldsymbol{0 < |x-a|} の部分は忘れがちなので注意しましょう。
実際, 0 = |x-a| すなわち x = a でも良いとすると, |f(a) - b | < \varepsilon が任意の \varepsilon > 0 で成立するため, f(a) = b となります。
このとき, \lim_{x\to a} f(x) = f(a) となるため,これは連続の定義になりますね。
以上の話をまとめると, 0 < | x - a| < \delta の 0 < |x-a| の部分を省くと,連続の定義になるということです。連続の定義を以下できちんと述べましょう。
関数の連続の定義
定義(関数の連続)
f\colon \mathbb{R} \to \mathbb{R}, \, a\in \mathbb{R} とする。このとき,
\lim_{x\to a} f(x) = f(a), \quad f(x) \longrightarrow f(a) \,\, (x\to a)
であるとは,
任意の \boldsymbol{\varepsilon > 0} に対して,ある \boldsymbol{ \delta > 0} が存在して,
\boldsymbol{ | x - a| < \delta \implies |f(x) - f(a)| < \varepsilon}
が成立することをいう。また,このとき f は x = a で連続 (continuous) であるという。
別の考え方をすれば,関数の極限の定義と連続の定義は 0 < |x-a| があるかどうかしか変わらないということです。従って本記事では, 0 < |x - a| の部分を省いた,連続の定義の方を採用し,これの意味と「お気持ち」を解説していくことにします。
なお,上を∀(全称記号,任意の)と∃(存在記号,存在する)の使い方を用いてかくと,
\color{red}\begin{aligned}&\forall \varepsilon>0 ,\exists \delta>0, \; |x-a|<\delta\implies |f(x)-f(a)|<\varepsilon \end{aligned}
とかけます(本記事ではこれは分からなくても読めます)。
ε-δ論法の言葉の意味と「お気持ち」
さて,上の定義の「言葉の意味」とその「感覚的な理解」(すなわち「お気持ち」)を順番に解説していきましょう。
ε-δ論法の言葉の意味
まずは「言葉の意味」を形式的に理解しましょう。定義を再掲します。
\varepsilon\text{-}\delta 論法(連続)
任意の \varepsilon > 0 に対して,ある \delta > 0 が存在して,
| x - a| < \delta \implies |f(x) - f(a) | < \varepsilon .それぞれの言葉の意味について,一覧にして解説してみましょう。
| ことば | 意味 |
|---|---|
| 任意の~ | 全ての,どんな~でも |
| ~に対して, | ~に応じて,~に依存して |
| ある~が存在して | 少なくとも一つ~を取ってこれる |
「任意の」「存在」の2つはもちろん大切ですが,見落としなのが「~に対して」の部分で,これは「~に依存して」という意味です。今回の場合, \delta>0 の取り方は \varepsilon > 0 に依存している, \varepsilon>0 に応じて変わってもよいということです。
なお,「ある~が存在して〇〇〇」という語順は,日本語では不自然ですが,英語の “There exists ~ such that 〇〇” に合わせたもので,「〇〇〇をみたす~が存在する」と同じ意味です。
これを踏まえて,定義を少しばかり平易に言い換えてみましょう。
どんなにテキトーな \varepsilon > 0 を取ってきても,それに応じて適切な \delta > 0 があって,
|x-a| < \delta \implies | f(x) - f(a) | < \varepsilonということが成立する。
さて,定義の「言葉の意味」はこんなところです。ある程度理解したものとして,次に「感覚的な理解」の部分である「お気持ち」を考えてみましょう。
ε-δ論法の「お気持ち」
再び定義を再掲します。
\varepsilon\text{-}\delta 論法(連続)
任意の \varepsilon > 0 に対して,ある \delta > 0 が存在して,
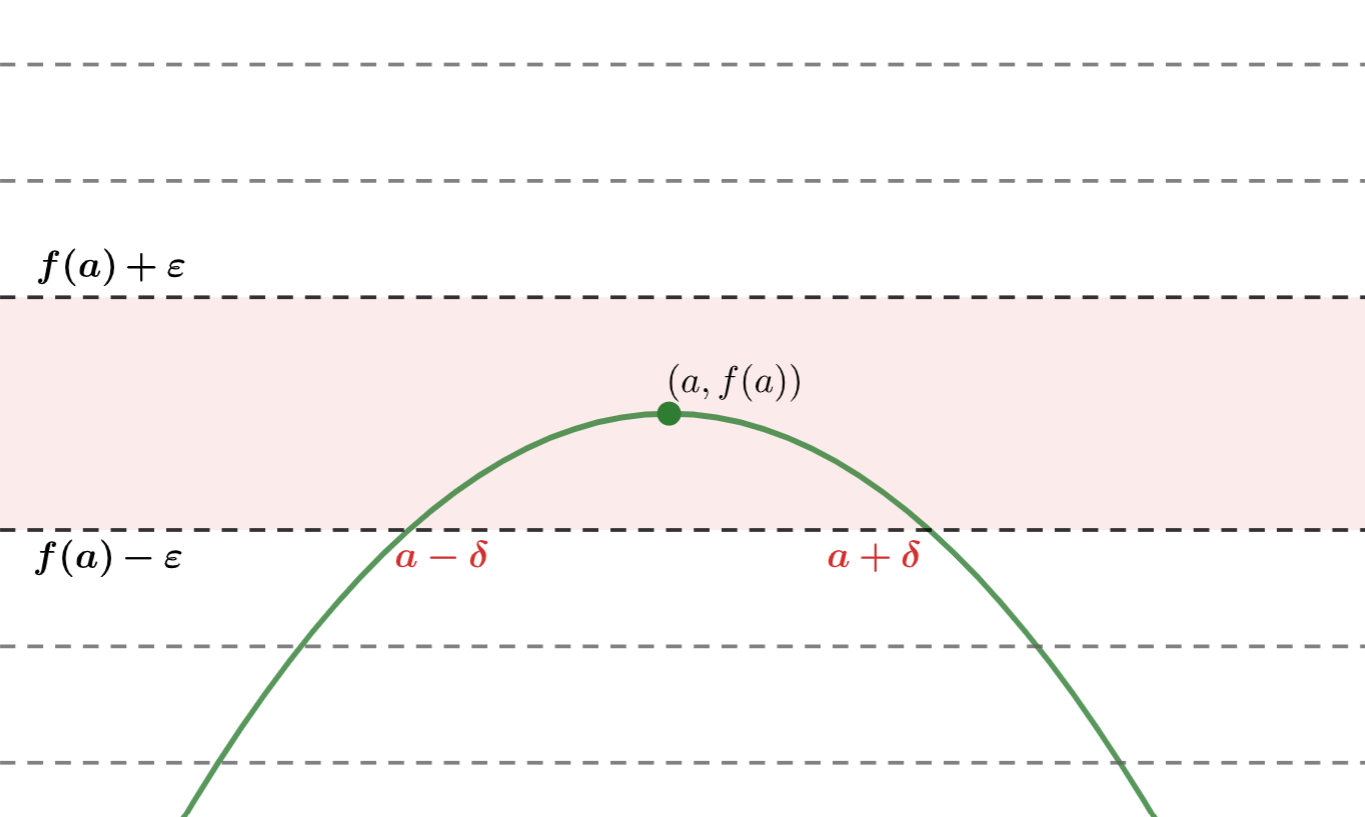
| x - a| < \delta \implies |f(x) - f(a) | < \varepsilon .さて最初に「任意の \varepsilon > 0 に対して」とあるので,まずはテキトーに \varepsilon > 0 を取ってみましょう。
このとき,「ある \delta> 0 が存在して | x - a| < \delta \implies |f(x) - f(a) | < \varepsilon 」なので,たとえば下の図のようになります。
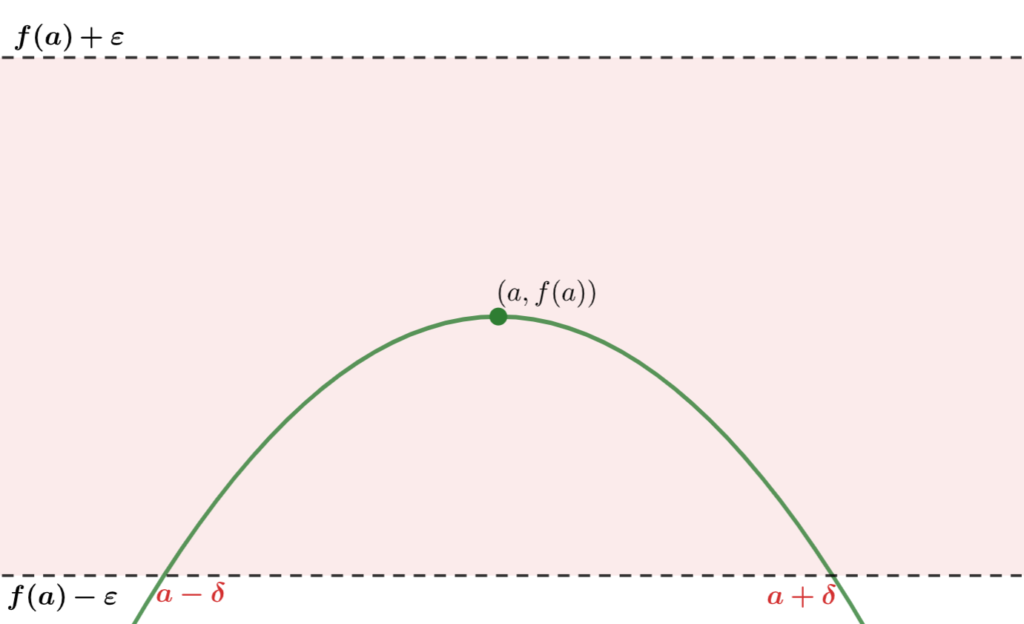
さて, \varepsilon > 0 は任意でしたから,もっと小さく取り直してみましょう。
すると,「これに応じて適切な」 \delta が再び存在します。このとき, |f(x)-f(a)| < \varepsilon の条件が「強くなった」分, \delta も必然的に小さくなることが分かるでしょう。
図で描くと以下のようなイメージです。
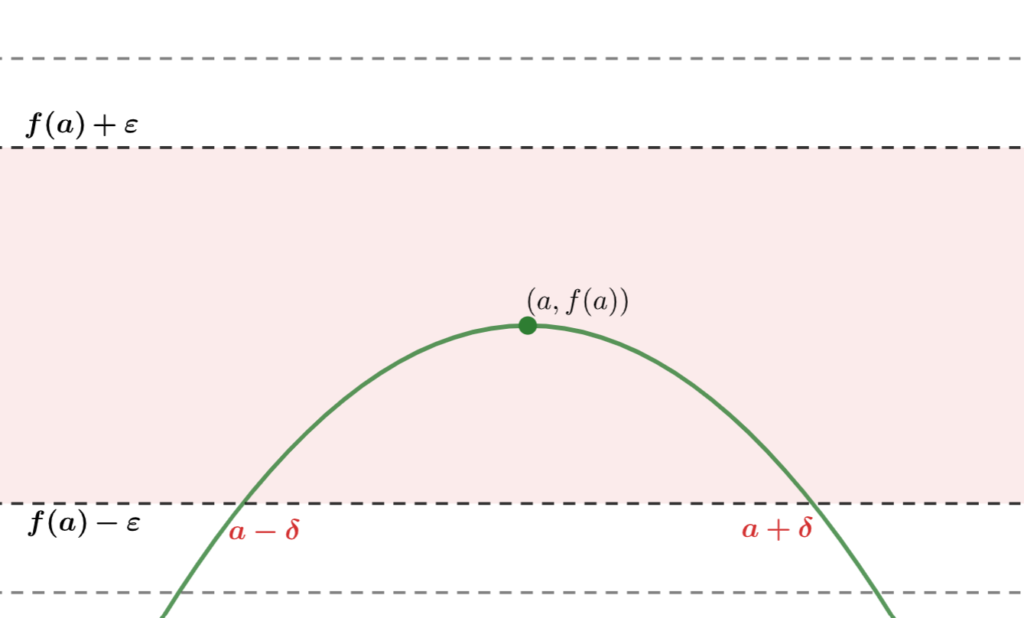
さらに \varepsilon > 0 をもっと小さくとってみましょう。再び「これに応じて」 \delta は小さくなり,図で描くと以下のようなイメージになります。
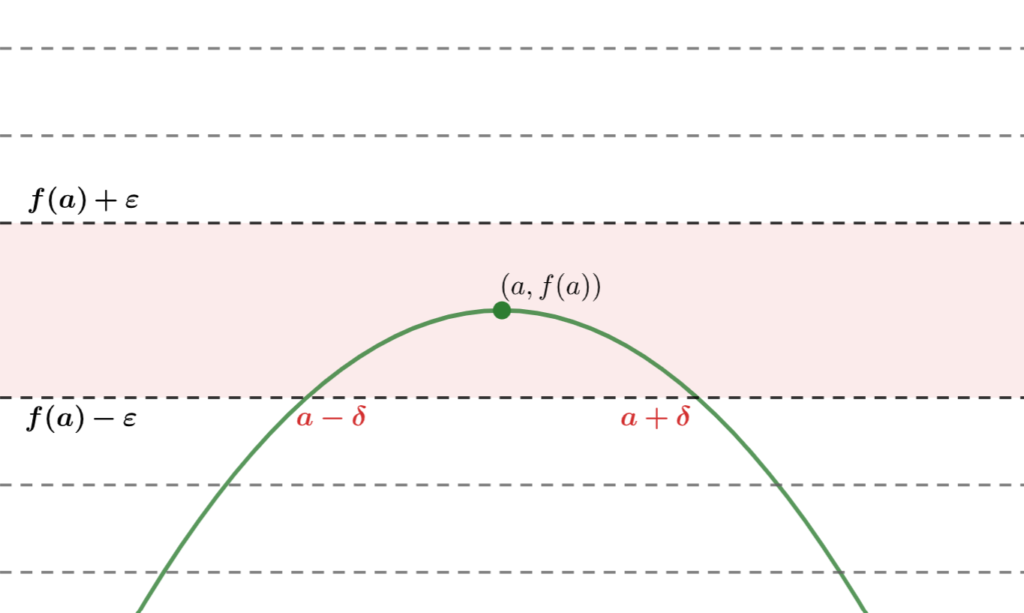
さて,これら3つの画像を見ると,
\delta> 0 が小さくなる \iff \varepsilon > 0 が小さくなる
ことが分かりますね。
|x-a| < \delta となる \delta > 0 が小さくなるということは, x が a に近づくことを意味し,
|f(x) - f(a) | < \varepsilon となる \varepsilon > 0 が小さくなるということは, f(x) が f(a) に近づくことを意味しますから,
「ラフ」に言うと
x が a に近づく \iff f(x) が f(a) に近づく
ということになりますね。
以上を踏まえて, \varepsilon\text{-}\delta 論法の「お気持ち」をまとめると,以下のようになります。
\varepsilon\text{-}\delta 論法は,「 x が a に近づくと, f(x) が f(a) に近づく」ことを意味する!
これは高校のときにやった,「感覚的な極限の定義」に一致していますね。これが \varepsilon\text{-}\delta 論法の意味の部分です。
具体例を用いて理解しよう
さて,具体例を用いて,より理解を深めましょう。扱う具体例は以下です。
例題
\displaystyle \color{red} \lim_{x\to 0 } x^4 = 0 を証明せよ。
まずテキトーな ε を取って考えてみよう
\varepsilon \text{-} \delta 論法を用いて,示すべきことを表現すると以下のようになります。
示すべきこと
任意の \varepsilon > 0 に対して,ある \delta> 0 が存在して,
|x|< \delta \implies |x^4| < \varepsilon.実際に証明する前に,まずテキトーな \varepsilon > 0 を取って考えて,イメージをつけましょう。
まず, \color{red} \varepsilon = 1 としましょう。たとえば, \color{red}\delta = 1 とすれば, |x|< \delta \implies |x^4| < \varepsilon. をみたしますね。
実際はもっと小さい \delta を取ることもできますが,「存在する」は一つでも取ればよいため,一つだけ具体例を示せばよいです。
\varepsilon をもっと小さく取ってみましょう。 \color{red} \varepsilon = 0.0001 とすると, \color{red} \delta = 0.1 とすればOKです。 \color{red} \varepsilon=0.00000001 とすると, \color{red} \delta=0.01 とすればよいことが分かるでしょう。
このように,どんな \varepsilon を取ってきても,それに応じて \delta を選ぶことができます。このことを実際に証明してみましょう。
厳密に証明してみよう
さて,厳密に証明してみましょう。示すべきことは,
示すべきこと
任意の \varepsilon > 0 に対して,ある \delta> 0 が存在して,
|x|< \delta \implies |x^4| < \varepsilon.であったことに注意してください。
証明
\varepsilon>0 を任意に取る。このとき, \color{red} \delta = \sqrt[4]{\varepsilon} とすると,
|x|< \delta \implies |x^4| < \varepsilon.
をみたすため,証明が終わる。
証明終
任意に取った \varepsilon > 0 に対し,条件をみたす \delta > 0 が「存在する」ことが示せたため,終わりました。
「存在する」はどうやって示したかというと,実際に \delta = \min\{\varepsilon, 1\} と取りました。
このように,「存在する」を示すときは,実際に具体的に取って見せるとよいです。
なお,今回は \delta = \sqrt[4]{\varepsilon} としましたが,もちろん \delta = \min\{\varepsilon, 1\} などでも良いです。
\delta の取り方は \varepsilon に依存して良いのでした。実際,依存していますね。
ε-δ論法の同値な表現
さて,ここで重要な補足をしておきましょう。 \varepsilon\text{-}\delta 論法の定義は,時と場合によって書き方が変わることがあります。
命題( \varepsilon\text{-}\delta 論法の同値な表現)
以下は全て同値である。
- 任意の \varepsilon > 0 に対し,ある \delta > 0 が存在して,0< |x-a|<\delta \implies | f(x) - b| < \varepsilon.
- 任意の \varepsilon > 0 に対し,ある \delta>0 が存在して, 0<|x-a|<\delta \implies | f(x) - b| < \textcolor{red}{\boldsymbol{k}} \varepsilon. ただし, k > 0 は \delta, \varepsilon に依存しない定数。
- 任意の \varepsilon > 0 に対し,ある \delta > 0 が存在して, 0<|x-a|<\delta \implies | f(x) -b| \textcolor{red}{\boldsymbol{\le}} \varepsilon.
- 任意の 0<\varepsilon \textcolor{red}{\boldsymbol{< l}} に対し,ある \delta > 0 が存在して,0< |x-a|<\delta \implies | f(x) - b| < \varepsilon. ただし, l > 0 は \delta,\varepsilon に依存しない定数。
- 任意の \varepsilon > 0 に対し,ある \delta>0 が存在して,0<|x-a|<\delta をみたす任意の x に対し,|f(x)-b| < \varepsilon が成立する。
- 任意の \varepsilon > 0 に対し,ある \delta \ge 1 が存在して,| f(x)-b| < \varepsilon \,\, (0<|x-a|<\delta) が成立する。
理屈は \varepsilon\text{-} N 論法のときと同じのため,省略します。
\varepsilon \text{-}\delta 論法はいろいろな形で登場するため,どの形で登場しても対応できるようにしましょう。
ε-δ論法の否定
\varepsilon\text{-}\delta 論法について,その否定,すなわち「\lim_{x\to a} f(x) =b でない」を考えたいときもあるでしょう。これの定義とお気持ちを述べましょう。
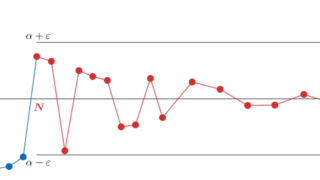
注意ですが,「\lim_{x\to a} f(x) =b でない」とは,他の値に収束していても良いですし,振動していても別に良いです。
否定の定義
否定を取るときのポイントは,主張における全ての「任意の」と「存在する」を入れ替えることです。上の 5. の否定を取ると考えるのが分かりやすいでしょう。
命題( \varepsilon\text{-}\delta 論法の否定)
数列 f(x) が x \to a のとき b に収束しないとは,
ある \varepsilon > 0 が存在して,任意の \delta>0 に対し,ある |x-a|<\delta をみたす x が存在して, |f(x) - b| \ge \varepsilon となることである。
元の定義との対応は以下のようになっています。
| 元の定義(上の5.を採用) | 否定の定義 |
|---|---|
| 任意の \varepsilon > 0 に対して, | ある \varepsilon > 0 が存在して, |
| ある \delta > 0 が存在して, | 任意の \delta> 0 に対して, |
| 0<|x-a|<\delta をみたす任意の x に対して | ある 0<|x-a|<\delta をみたす x が存在して, |
| |f(x) - b | < \varepsilon. | |f(x) - b| \ge \varepsilon. |
「任意の」と「ある~が存在して」が真逆になっており,最後の不等号の向きも逆になっていますね。
なお語順により,否定の定義の3行目の x の取り方は, \varepsilon, \delta に依存して構いません。
否定のお気持ち
否定の意味は以下の通りです。
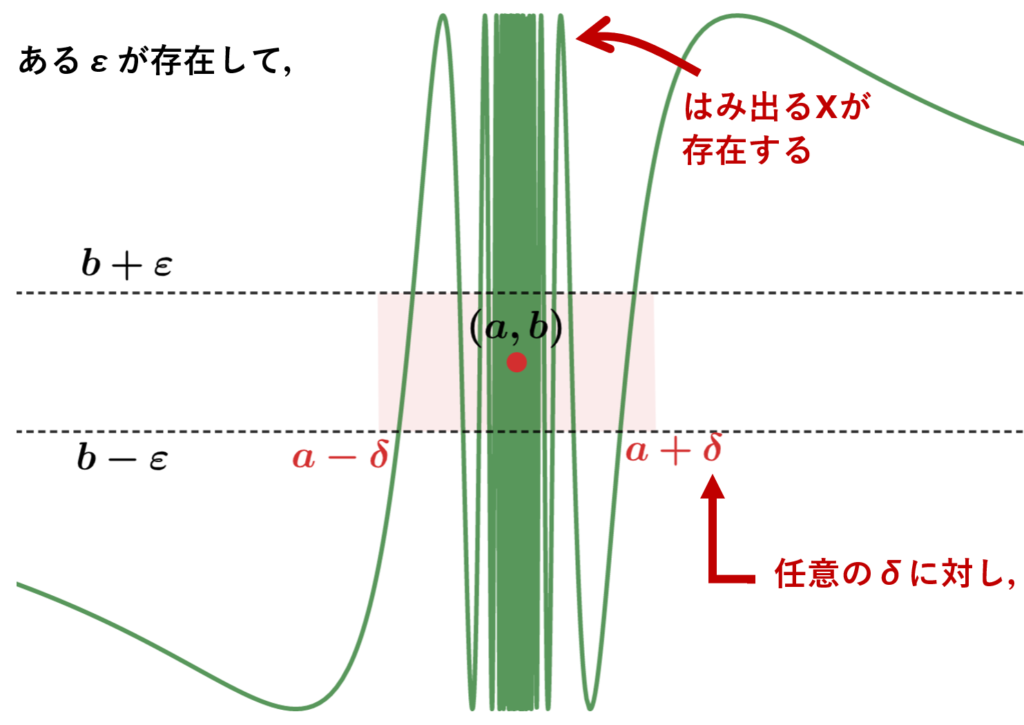
上は振動の例ですが,実際には「他の値に収束する」「 \pm\infty に発散する」という場合もあることに注意してください。
∞を含むε-δ論法の定義
さて,これまで扱ってきた定義は, a, b= \lim_{x\to a} f(x) がともに有限であるものでした。では,無限大やマイナス無限大に発散する場合の定義はどうなるのかについて,表にまとめておきましょう。
| 表現 | ε-δ論法による定義 |
|---|---|
| \lim_{x\to a} f(x) = b | 任意の \varepsilon>0 に対して,ある \delta > 0 が存在して, 0 < |x-a| < \delta \implies |f(x) - b| < \varepsilon. |
| \lim_{x\to a} f(x) = \infty | 任意の K >0 に対して,ある \delta > 0 が存在して, 0 < |x-a| < \delta \implies f(x) > K. |
| \lim_{x\to a} f(x) = -\infty | 任意の K >0 に対して,ある \delta > 0 が存在して, 0 < |x-a| < \delta \implies f(x) <- K. |
| \lim_{x\to \infty} f(x) = b | 任意の \varepsilon>0 に対して,ある L > 0 が存在して, x > L \implies |f(x) - b| < \varepsilon. |
| \lim_{x\to -\infty} f(x) = b | 任意の \varepsilon>0 に対して,ある L > 0 が存在して, x < -L \implies |f(x) - b| < \varepsilon. |
| \lim_{x\to \infty} f(x) = \infty | 任意の K>0 に対して,ある L > 0 が存在して, x > L \implies f(x) > K. |
| \lim_{x\to \infty} f(x) = -\infty | 任意の K>0 に対して,ある L > 0 が存在して, x > L \implies f(x) < -K. |
| \lim_{x\to -\infty} f(x) = \infty | 任意の K>0 に対して,ある L > 0 が存在して, x < - L \implies f(x) > K. |
| \lim_{x\to -\infty} f(x) = -\infty | 任意の K>0 に対して,ある L > 0 が存在して, x < - L \implies f(x) < -K. |
\delta, \varepsilon は主に「微小量」を意味するため,「大きな変数」を意味する際には K, L, M, N,R などが用いられることが多いです。
\pm\infty を含む場合についての「お気持ち」の解説は行わないことにします。自分で理解してみましょう。数列の極限( \varepsilon\text{-}N 論法)の方では無限大を含む場合についても扱っているため,そちらも参考になるかもしれません(→ イプシロンエヌ論法をわかりやすく丁寧に~数列の極限の定義~)。
左極限・右極限
左極限・右極限の定義
さて, x\to a と書いたときは, x < a と x> a の両側から近づけることを考えました。一方で,常に x< a をみたすように近づけることを x\to a- などとかき,これを左極限,逆に常に x> a をみたすように近づけることを x \to a+ などとかき,これを右極限と言います。
これも \varepsilon \text{-} \delta 論法を用いて定義しておきましょう。
定義(左極限・右極限)
f\colon \mathbb{R} \to \mathbb{R}, \, a\in \mathbb{R} とする。このとき,
\lim_{x\to a-} f(x) = b, \quad f(x) \longrightarrow b \,\, (x\to a-)とは,
任意の \boldsymbol{\varepsilon > 0} に対して,ある \boldsymbol{ \delta > 0} が存在して,
\boldsymbol{0 < a-x < \delta \implies |f(x) - b| < \varepsilon}
が成立することをいう。このときの b を x\to a - としたときの f の左極限 (left limit) という。
また,
\lim_{x\to a+} f(x) = b, \quad f(x) \longrightarrow b \,\, (x\to a+)とは,
任意の \boldsymbol{\varepsilon > 0} に対して,ある \boldsymbol{ \delta > 0} が存在して,
\boldsymbol{0 < x-a < \delta \implies |f(x) - b| < \varepsilon}
が成立することをいう。このときの b を x\to a + としたときの f の右極限 (right limit) という。
0 < |x-a| <\delta の部分がそれぞれ 0 < a-x < \delta,\,\, 0 < x-a < \delta に変わっていますね。これにより片側しか考えないことができます。
なお,\color{red} x \to a- の部分は \color{red} x\to a-0, \,\, x\uparrow a などと書かれることもあります。同様に, \color{red} x\to a+ は, \color{red} x\to a+0, \,\, x\downarrow a と書いても同じ意味です。
定義より「左極限かつ右極限をもつ \implies 極限をもつ」 ことが従います。
左連続・右連続の定義
上記において, \lim_{x\to a-} f(x) = f(a) が成立するとき,f は a で左連続 (left continuous) といい, \lim_{x\to a+} f(x) = f(a) が成立するとき,右連続 (right continuous) といいます。
\varepsilon\text{-}\delta 論法で述べる際は, 0 < a-x < \delta, \,\,0 < x-a < \delta をそれぞれ 0 \le a-x < \delta, \,\,0 \le x-a < \delta に変えるだけです。
定義より,「左連続かつ右連続 \implies 連続」 であることが従います。
関数の極限の性質
関数の極限には以下の性質があります。
定理(関数の極限の性質)
以下, f , g \colon \mathbb{R} \to \mathbb{R} とし, a\in [-\infty,\infty],\, b, b_1, b_2 \in \mathbb{R} とする。このとき,
- \displaystyle b_1 = \lim_{x\to a} f(x), b_2 = \lim_{x\to a} f(x) ならば b_1 = b_2 である。すなわち,極限は存在すれば一意に定まる。
- \displaystyle b_1 = \lim_{x\to a} f(x), \, b_2 = \lim_{x\to a} g(x) ならば,
- \displaystyle b_1 + b_2 = \lim_{x\to a} (f(x)+g(x)),
- \displaystyle b_1b_2 = \lim_{x\to a} (f(x)g(x)).
- b =\lim_{x\to a} f(x) \ne 0 ならば, \displaystyle \frac{1}{b} = \lim_{x\to a} \frac{1}{f(a)}.
これの証明は,以下の記事が参考になると思います。
なお,数列の収束とは以下の関係があります。
定理(関数の収束 \iff 数列の収束)
f \colon \mathbb{R} \to \mathbb{R}, \,\, a\in \mathbb{R} とする。このとき,
- \displaystyle \lim_{x\to a} f(x) = b
\iff
\displaystyle a_n \ne a, \lim_{n\to\infty} a_n = a となる任意の数列 \{a_n\} に対して,\displaystyle \lim_{n\to\infty} f(a_n) = b - \displaystyle \lim_{x\to a} f(x) 収束する
\iff
\displaystyle a_n \ne a, \lim_{n\to\infty} a_n = a となる任意の数列 \{a_n\} に対して,\displaystyle \lim_{n\to\infty} f(a_n) が収束する
これは,以下が参考になると思います。
おわりに
\varepsilon\text{-}\delta 論法は,解析学における最初の登竜門であり,大学数学の難しさを痛感する部分だといえるでしょう。
すぐに理解できる必要はありません。ちゃんと勉強していれば,いずれ分かるようになります。大事なのは,逃げずにしっかりと自分の頭で考えることです。焦らずにゆっくりと前へ進んでいきましょう。
とりあえず,ここまでおつかれさまでした。