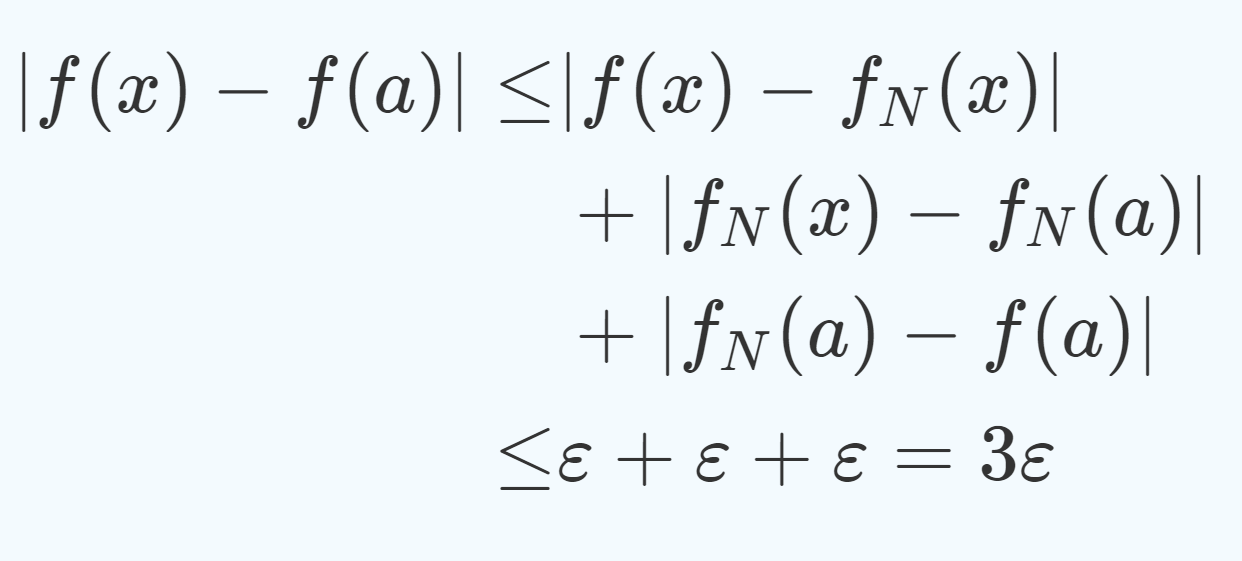一様収束 (uniformly convergence) と各点収束 (pointwise convergence) の顕著な違いとして,連続関数列の極限が再び連続関数になるという性質が挙げられます。このことの証明と,なぜ一様収束でないとこの性質が言えないのかを考えてみましょう。
連続関数列の一様収束極限は必ず連続関数になる
定理1(連続関数列の一様収束極限は連続)
\{f_n\} は [0,1] 上で定義された連続関数の列とし, f に一様収束するとする。このとき, f は [0,1] 上連続である。
f_n\colon [0,1]\to \R または f_n\colon [0,1]\to \mathbb{C} です。一様収束なので,任意の \varepsilon >0 に対し,ある N\ge 1 が存在して, x \in [0,1] に関係なく
n\ge N\implies |f_N(x)-f(x)|<\varepsilon
が成り立つということです。
これは,各点収束では言えない,一様収束ならではの性質です。各点収束では言えない例については,たとえば,上リンク先の記事の例3を参照してください。
連続関数列の一様収束極限は必ず連続関数になることの証明
定理1の証明
\varepsilon > 0,\,a \in [0, 1] を固定する。一様収束することから,ある N \ge 1 が存在して,(★)
|f_N(x) - f(x) | < \varepsilon, \quad x \in [0,1]
が成立する。 f_N は連続であるから,ある \delta > 0 が存在して,
が成立する。以上を踏まえて, x \in [0, 1] が |x-a| < \delta をみたすならば,三角不等式より,
となるから, f は連続である。
証明終
さて,この証明で一様収束を用いているのはどこでしょうか。一様収束が各点収束に変わるとどこが問題になるのでしょうか。
一様収束を用いているのは,上の (★) の部分です。 |f(x) - f_N(x) | < \varepsilon が任意の x \in [0,1] について成立することがポイントです。
最後の三角不等式のところで, |x - a| < \delta をみたす任意の x \in [0,1] に対して, | f(x) - f_N(x)| < \delta であることを用いていますが,これができるのは (★) の一様収束性があるからですね。
より一般の位相空間における定理
より高度な,位相空間から距離空間における写像の列の一様収束について考えましょう。
定理2(より一般の一様収束定理)
(X,\mathcal{O}) を位相空間とし, (Y,d) を完備距離空間とする。 C(X,Y) を,連続写像 f\colon X\to Y 全体の集合とし,一様距離
d_\infty(f,g)=\min\left\{\sup_{x\in X} d\bigl(f(x), g(x)\bigr), 1\right\}雑に言うと, \{f_n\}\subset C(X,Y) が一様距離によって収束(一様収束)すれば, f\in C(X,Y) すなわち f も連続だということです。厳密には,「 \{f_n\}\subset C(X,Y) が d_\infty におけるコーシー列であれば」という方が正しいです。
C(X,Y) が距離空間であることは簡単だし,今ここでの本質ではないので,完備性のみ示します。
完備性の証明
\{f_n\}\subset C(X,Y) が d_\infty におけるコーシー列であるとする。すると,各 x\in X に対し, \{f_n(x)\}\subset Y は d におけるコーシー列であるから, Y の完備性より
f(x)=\lim_{n\to\infty} f_n(x)
が存在し,これにより,写像 f\colon X\to Y が構成できる。 f が連続であることを示せばよい。以下,記号を乱用して, C(X,Y) の元でないかもしれない写像 f にも d_\infty を用いる(定義は上の定理2の式の通り)。
\varepsilon >0,\, a\in X を固定する。 \{f_n\} が d_\infty におけるコーシー列なので,ある N\ge 1 が存在して, d_\infty(f_N,f)\le \varepsilon とできる。 f_N は連続なので, a のある開近傍 a\in U_a が存在して,
x\in U_a \implies d\bigl(f_N(x), f_N(a)\bigr)\le \varepsilon
とできる。ここで, x\in U_a に対し,三角不等式により,
であるから, f\in C(X,Y) が示せた。
証明終
後半の三角不等式のところは,前半の f\colon [0,1]\to \R (\text{or }\mathbb{C}) のときの証明と同じような感じですね。