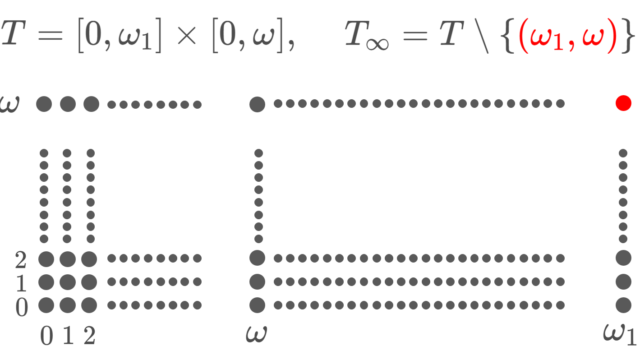 集合と位相
集合と位相 【位相空間】チコノフの板(Tychonoff Plank)
チコノフの板とは,順序位相の直積空間であり,T4だがT5でない空間の例として,あるいは正規だが completely 正規でない空間の例として紹介されます。チコノフの板について,その位相的性質を解説しましょう。
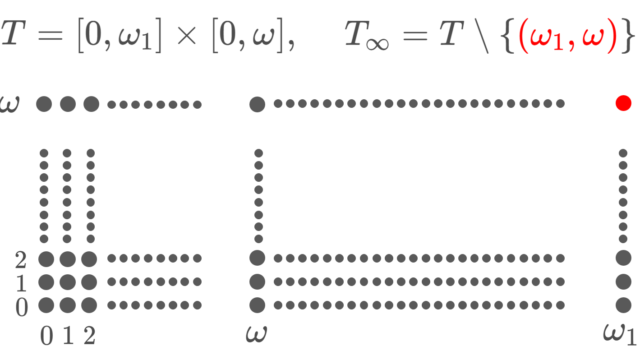 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相 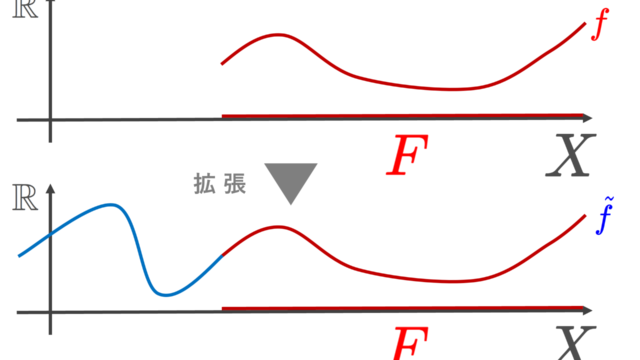 集合と位相
集合と位相 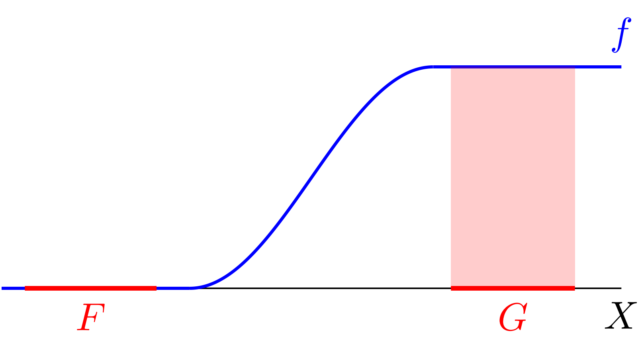 集合と位相
集合と位相 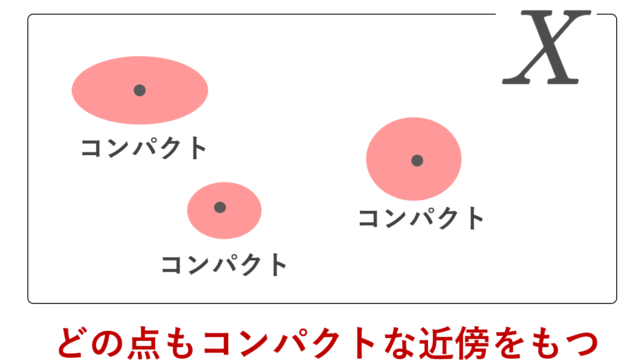 集合と位相
集合と位相  集合と位相
集合と位相 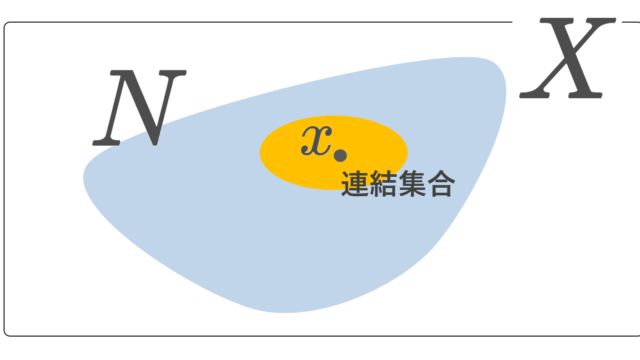 集合と位相
集合と位相  集合と位相
集合と位相