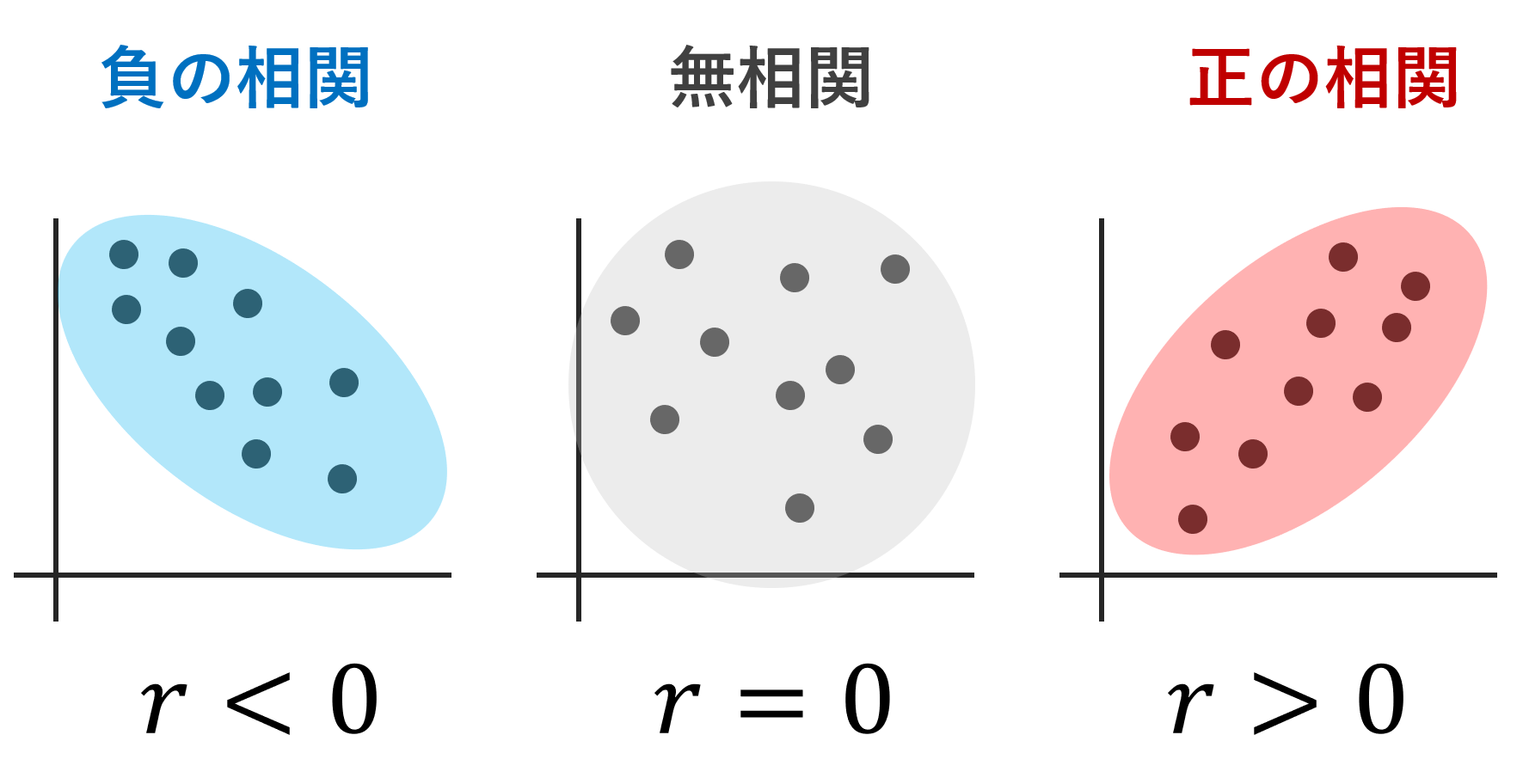
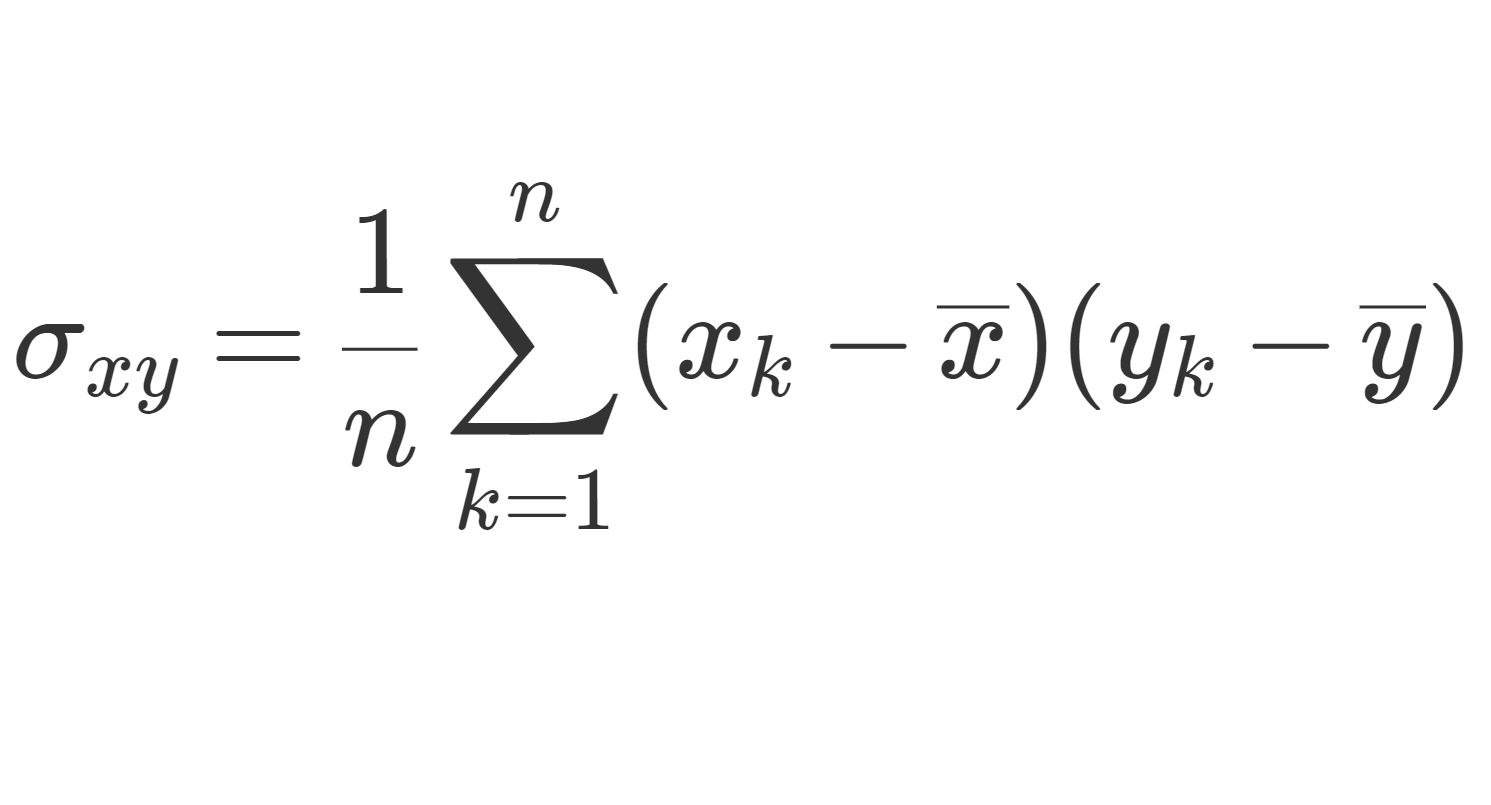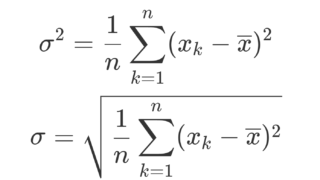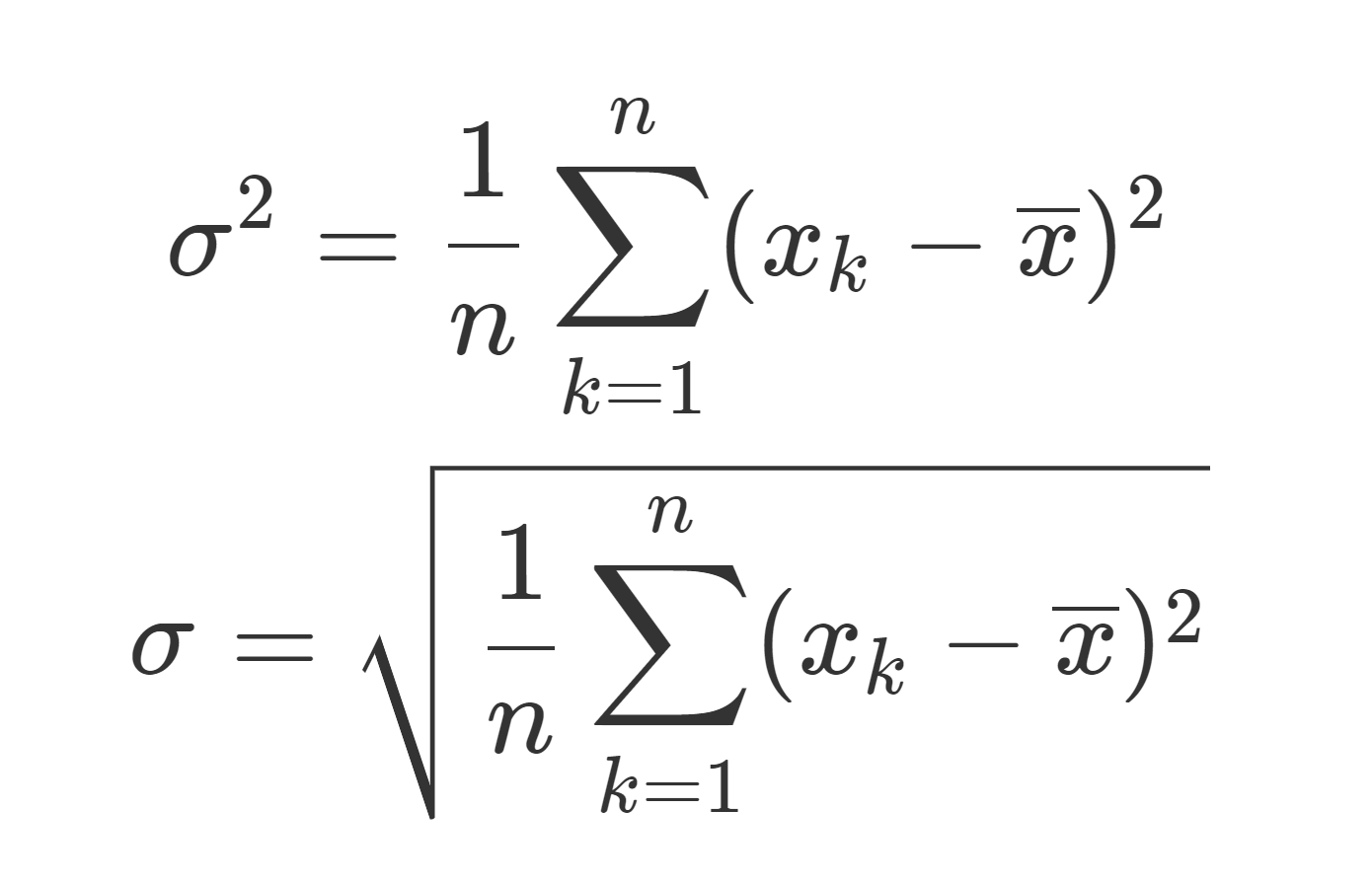データ (x_1,y_1),(x_2,y_2)\dots,(x_n,y_n) における共分散は
\sigma_{xy} =\frac{1}{n}\sum_{k=1}^n (x_k-\overline{x})(y_k-\overline{y})
と定義されます。共分散ついて定義を詳しく述べ,求め方の具体例から性質までを順番に述べましょう。
共分散の定義と具体例
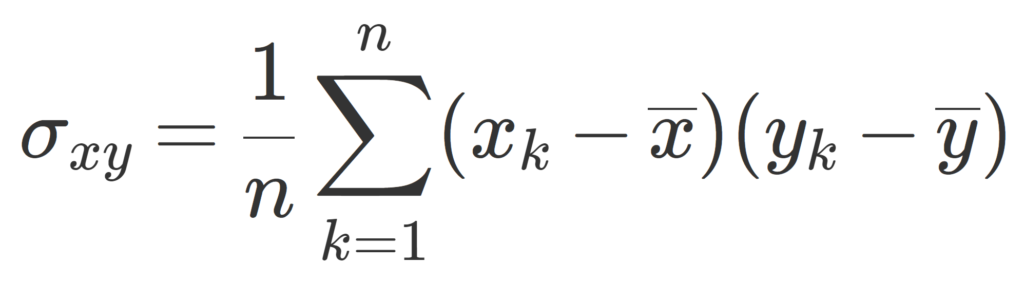
共分散の定義
定義(共分散)
2つずつがセットになったデータ (x_1,y_1),(x_2,y_2),\dots, (x_n,y_n) について, \overline{x}=\frac{1}{n}\sum_{k=1}^n x_k,\; \overline{y} = \frac{1}{n}\sum_{k=1}^n y_k を各成分の平均とする。このとき,
\color{red}\large\sigma_{xy} =\frac{1}{n}\sum_{k=1}^n (x_k-\overline{x})(y_k-\overline{y})
を2つのデータの共分散 (covariance) という。
共分散とは,各成分の平均からの偏差 x_k-\overline{x}, y_k-\overline{y} の積 (x_k-\overline{x})(y_k-\overline{y}) の平均なわけですね。
なお,
\sigma_{xx} = \frac{1}{n}\sum_{k=1}^n (x_k-\overline{x})^2=\sigma_x^2
ですから, x_k=y_k とすると,共分散は x の分散の定義に一致しますね(→データの分散・標準偏差の定義・具体例・性質まとめ)。また, \sigma_{xy}=\sigma_{yx} も明らかです。
共分散の性質
具体例を挙げる前に,覚えておくべき性質を述べましょう。
定義(共分散の性質)
データ (x_1,y_1),(x_2,y_2),\dots, (x_n,y_n) の共分散について
\color{red}\large \sigma_{xy} = \overline{xy}-\overline{x}\,\overline{y}.
ただし,\overline{xy} =\frac{1}{n} \sum_{k=1}^n x_ky_k は積 x_1y_1, x_2y_2,\dots, x_ny_n の平均を表す。
共分散は ( xy の平均)ー( x の平均)( y の平均)でも求められるということですね。
なお,分散は \sigma_x^2=\overline{(x^2)}-(\overline{x})^2 ((2乗の平均)ー(平均の2乗)) でも求められました(→データの分散・標準偏差の定義・具体例・性質まとめ)が,本定理はそれと対応しているのが分かるでしょう。
証明は簡単です。
証明
\begin{aligned}&\frac{1}{n} \sum_{k=1}^n (x_k-\overline{x})(y_k-\overline{y})\\ &= \frac{1}{n} \sum_{k=1}^n ( x_ky_k-\overline{x}y_k-\overline{y}x_k+\overline{x}\,\overline{y}) \\&= \frac{1}{n} \left\{\sum_{k=1}^n x_ky_k -\overline{x}\sum_{k=1}^n y_k -\overline{y}\sum_{k=1}^n x_k\right\} +\overline{x}\,\overline{y}\\ &= \overline{xy}-\overline{x}\,\overline{y}-\overline{y}\,\overline{x}+\overline{x}\,\overline{y} \\ &= \overline{xy}-\overline{x}\,\overline{y} . \end{aligned}証明終
共分散の具体例
共分散を,上の定義と定理の両方の方法で求めてみましょう。
例題.
5人の数学のテストの点数・理科のテストの点数は以下のようになっている。
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 数学 | 30 | 40 | 70 | 80 | 80 |
| 理科 | 100 | 30 | 60 | 70 | 90 |
このとき,5人の数学の点数と理科の点数の共分散を求めよ。
表を書いて順番に考えていきましょう。
\sigma_{xy} = \frac{1}{n}\sum_{k=1}^n (x_k-\overline{x})(y_k-\overline{y}) と \sigma_{xy} = \overline{xy} - \overline{x}\,\overline{y} の両方で求めることを考えます。
| k | 1 | 2 | 3 | 4 | 5 | 平均 \frac{1}{5}\sum_{k=1}^5 \fbox{\phantom{1}} |
|---|---|---|---|---|---|---|
| x_k | 30 | 40 | 70 | 80 | 80 | \overline{x}= 60 |
| y_k | 100 | 30 | 60 | 70 | 90 | \overline{y}= 70 |
| x_k-\overline{x} | -30 | -20 | 10 | 20 | 20 | 0 |
| y_k-\overline{y} | 30 | -40 | -10 | 0 | 20 | 0 |
| (x_k-\overline{x})(y_k-\overline{y}) | -900 | 800 | -100 | 0 | 400 | \sigma_{xy}= 40 |
| x_ky_k | 3000 | 1200 | 4200 | 5600 | 7200 | \overline{xy} = 4240 |
定義通りに求めるのは上の赤字ですね。一方で,定理を用いると上の表より
\sigma_{xy} = \overline{xy}-\overline{x}\,\overline{y} = 4240-60\cdot 70=\textcolor{red}{\boldsymbol{40}}
と同じ値が求められますね。実際には求めやすい方で求めればよいです。
データの様子を散布図で見ておきましょう。各点の値は (x_k-\overline{x})(y_k-\overline{y}) の値を記しています。
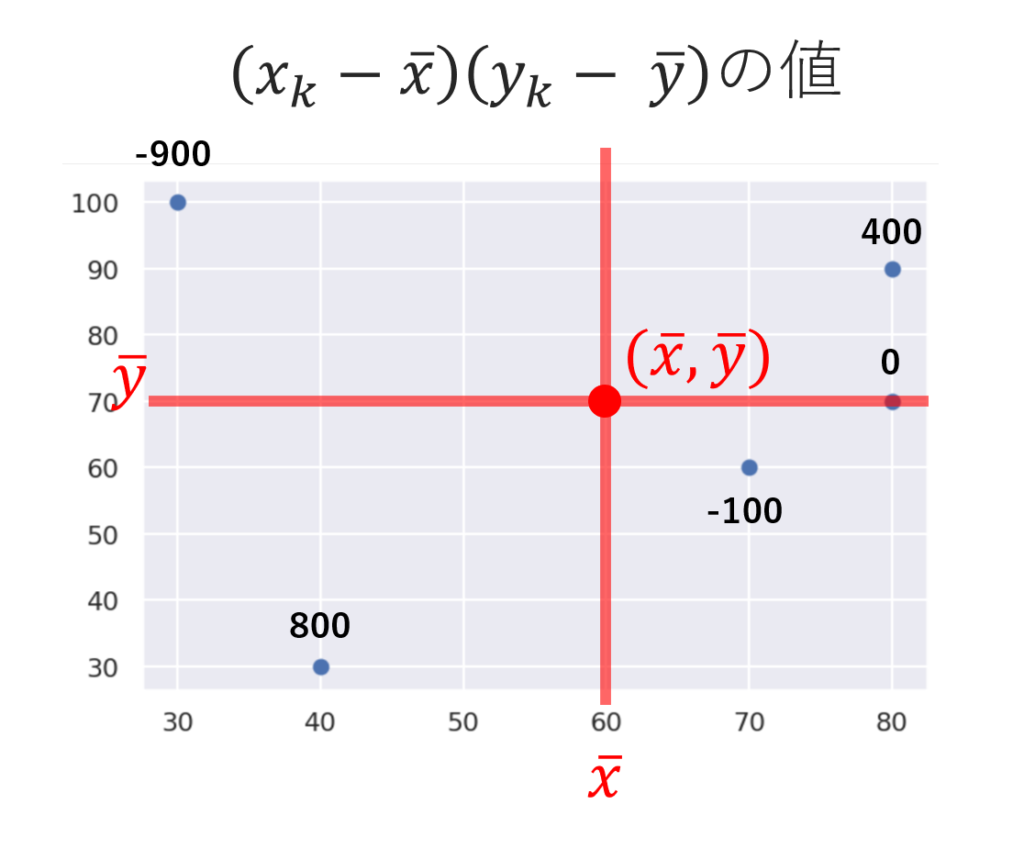
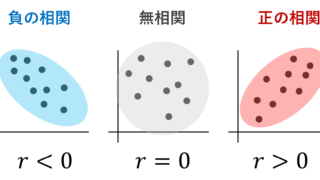
上図からもわかるように, (x_k-\overline{x})(y_k-\overline{y}) の符号は以下の図のように定まりますね。
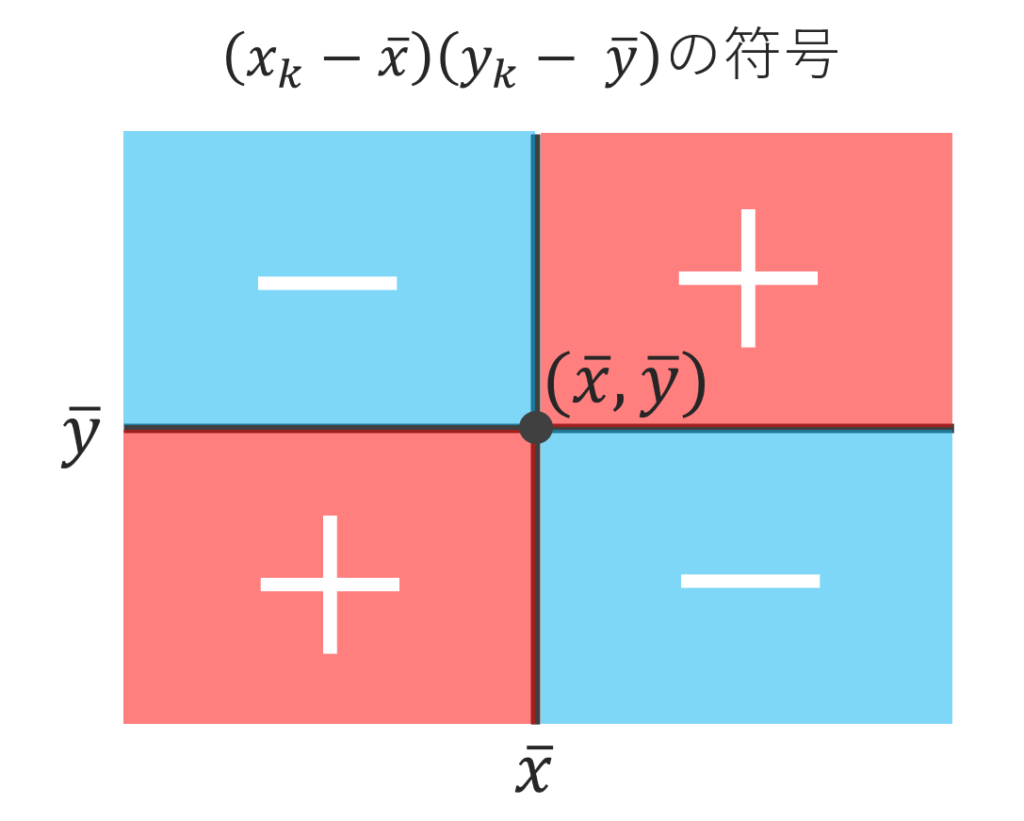
平均 (\overline{x}, \overline{y}) を中心として,左下から右上がりに点があるときは正で,左上から右下がりに点があるときは負になるわけですね。今回の例題では,正のものも負のものもありますが,共分散自体は正なので,ざっくりいうと「正のものの方がちょっと強い」といえます。
このように,共分散の符号を見ることで,データが,上図のどの領域に多く広がっているかということが何となくわかります。
共分散と変量の変換
変量を変換したときに共分散がどう変わるか考えておきましょう。
定理(共分散と変量の変換)
データ (x_1, y_1), \dots, (x_n,y_n) に対して,
\begin{aligned}X_k &= a_1x_k +b_1, \\ Y_k &= a_2y_k +b_2 \end{aligned}
とデータを変換したとき, (X_1,Y_1),\dots, (X_n,Y_n) の共分散について
が成り立つ。
本定理から,データのスケールを変えると(データ全体を何倍かすると),共分散も変わってしまうことが分かりますね。このこともわかるように,共分散は,別のデータのもの同士の大小を比較してもあんまり意味がありません。共分散は,値そのものが大事というわけではありません。
証明は簡単です。
証明
\overline{X}=a_1\overline{x}+b_1,\, \overline{Y}=a_2\overline{y}+b_2 であることに注意して,
\begin{aligned}\sigma_{XY} &= \frac{1}{n}\sum_{k=1}^n(X_k-\overline{X})(Y_k-\overline{Y}) \\ &= \frac{1}{n} \sum_{k=1}^n (a_1x_k-a_1\overline{x})(a_2y_k-a_2\overline{y})\\ &= a_1a_2 \frac{1}{n}\sum_{k=1}^n(x_k-\overline{x})(y_k-\overline{y})\\ &= a_1a_2 \sigma_{xy} . \end{aligned}証明終
共分散から相関係数へ
上で,共分散は値そのものを比較する意味はあまりないと述べました。しかし,上手く数値を比較したいと思うでしょう。そこで考えられるのが相関係数 (correlation coefficient) です。相関係数は標準偏差 \sigma_x, \sigma_y と共分散 \sigma_{xy} を用いて
r = \frac{\sigma_{xy}}{\sigma_x\sigma_y}
と定義されます。各々の標準偏差で割ってあげることで,上手くスケールを「合わせて」あげるわけです。これについては,以下で解説しています。