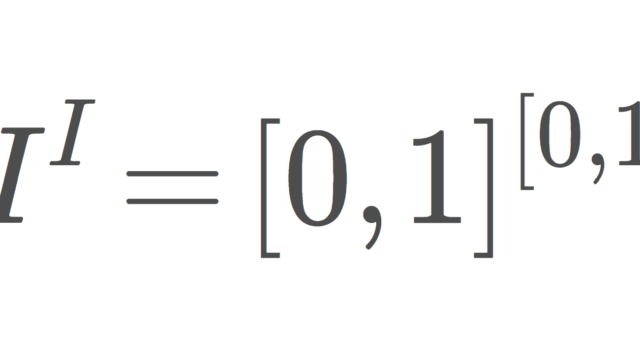 集合と位相
集合と位相 I^I の位相的性質~コンパクトだが点列コンパクトでない例~
I=[0,1]を単位区間とします。このとき,I^Iとは,関数f: I → I全体の集合を指します。I^Iにおける直積位相を考えると,これはコンパクトだが点列コンパクトでない位相空間の代表例です。I^Iの位相的性質を解説しましょう。
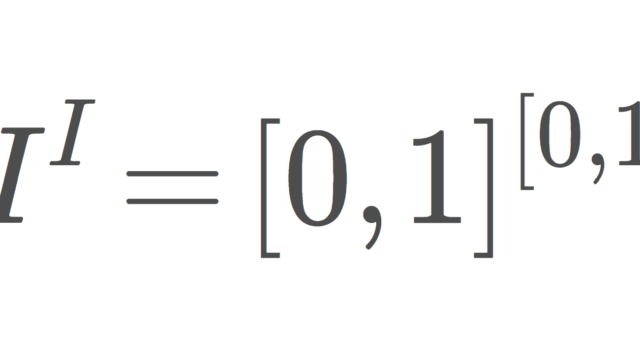 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相