 集合と位相
集合と位相 【誘導位相】始位相と終位相
「位相空間の間の写像が連続写像になる」という話を転換して,「間の写像が連続になるよう位相空間を定める」という議論を行うのが,誘導位相の考え方です。定義域側に定まる位相を始位相,終域側に定まる位相を終位相といいます。本記事では,始位相・終位相の定義と具体例,普遍性と呼ばれる性質を紹介します。
 集合と位相
集合と位相  本・サイトの紹介
本・サイトの紹介  本・サイトの紹介
本・サイトの紹介  本・サイトの紹介
本・サイトの紹介  本・サイトの紹介
本・サイトの紹介 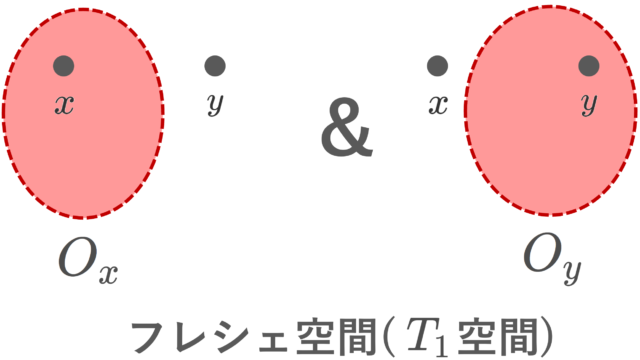 集合と位相
集合と位相 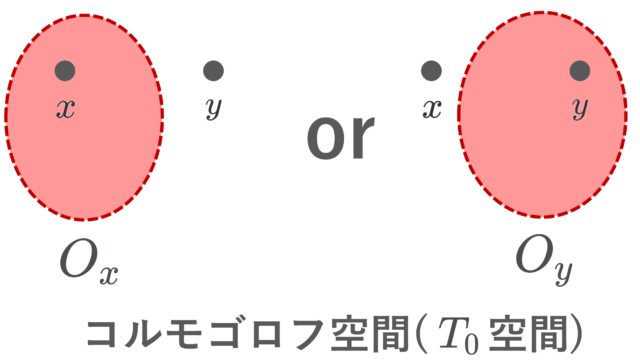 集合と位相
集合と位相 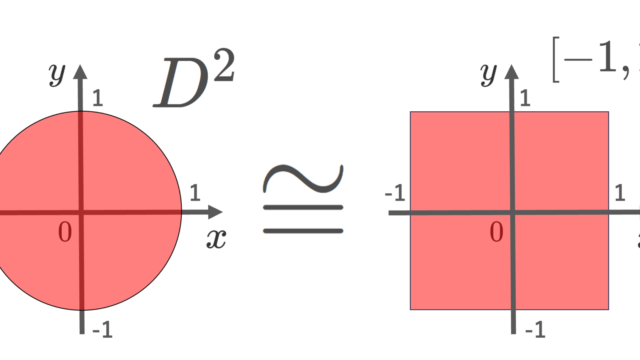 集合と位相
集合と位相 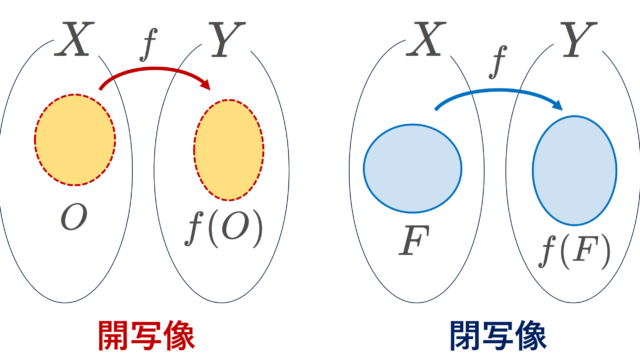 集合と位相
集合と位相 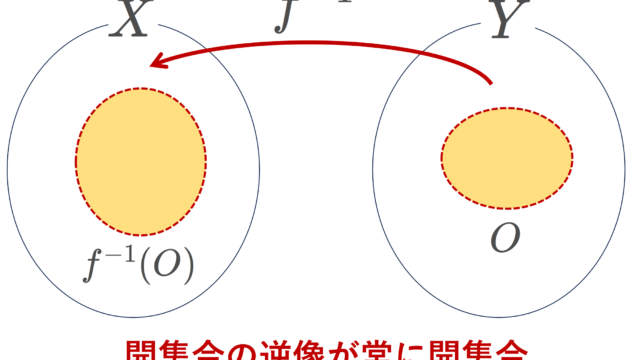 集合と位相
集合と位相