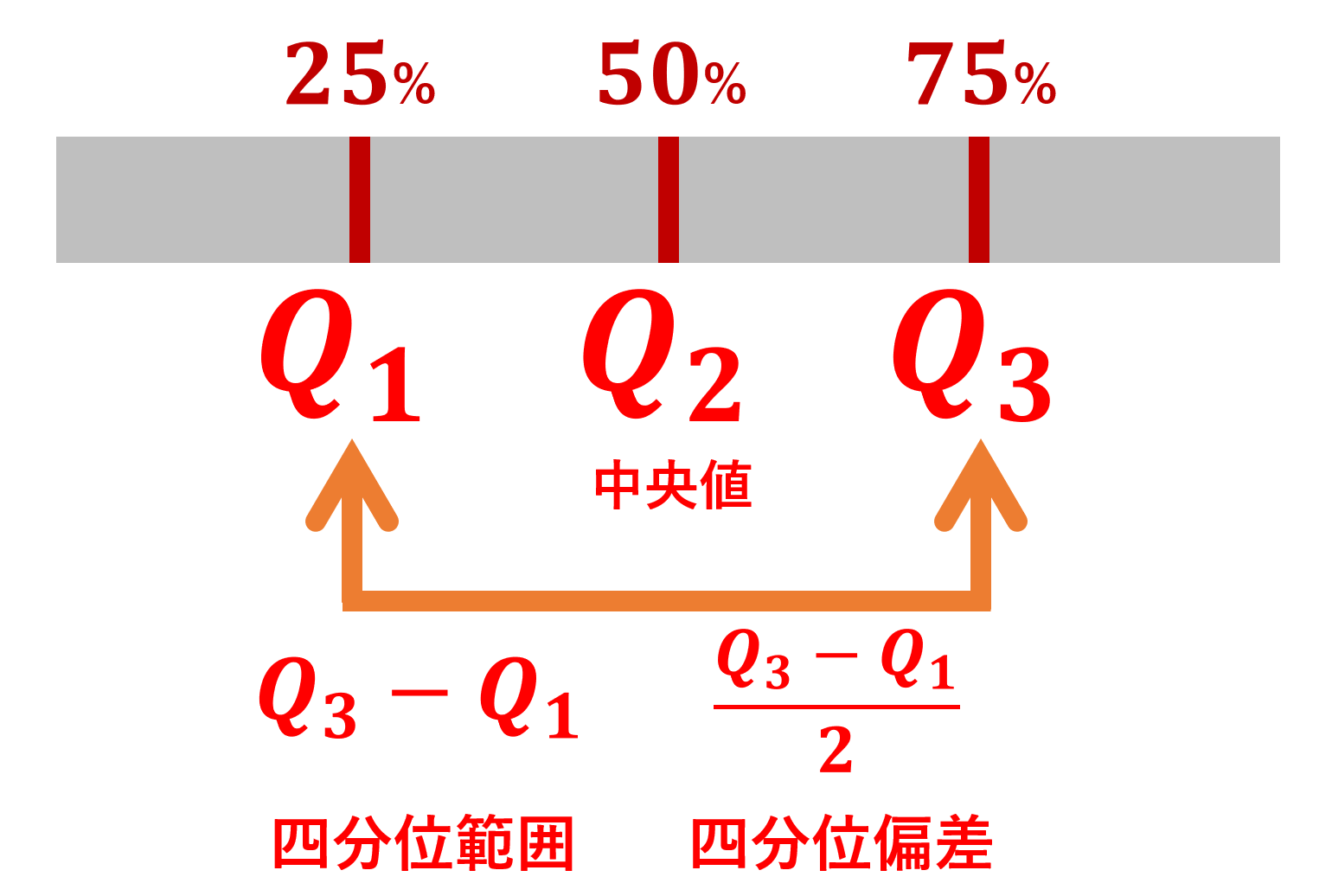
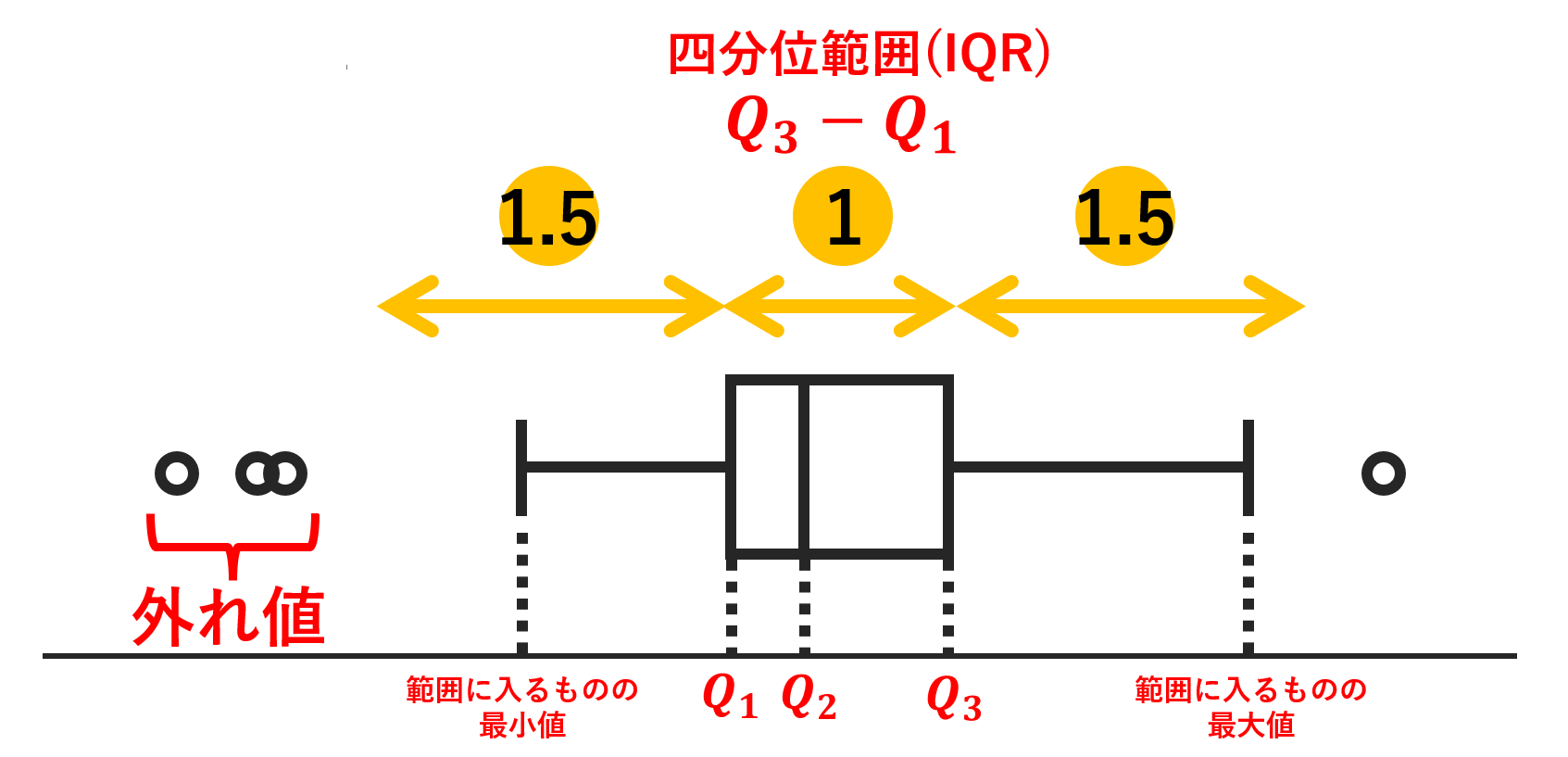
データを昇順に並べ,4等分したときの境界にあたる3つの数を「四分位数」といい,この3つの数のうち一番大きいものから一番小さいものを引いたのを「四分位範囲」,四分位範囲を2で割ったものを「四分位偏差」といいます。
四分位数・四分位範囲・四分位偏差について,図を交えて解説しましょう。
四分位数・四分位範囲・四分位偏差とは
四分位数とは,データを昇順に4つに分けるものですが,定義には「中央値」の概念が必要です。まずこれについて復習しましょう。
中央値の復習
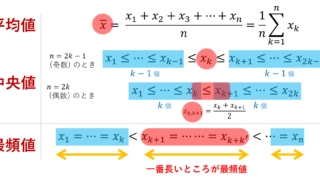
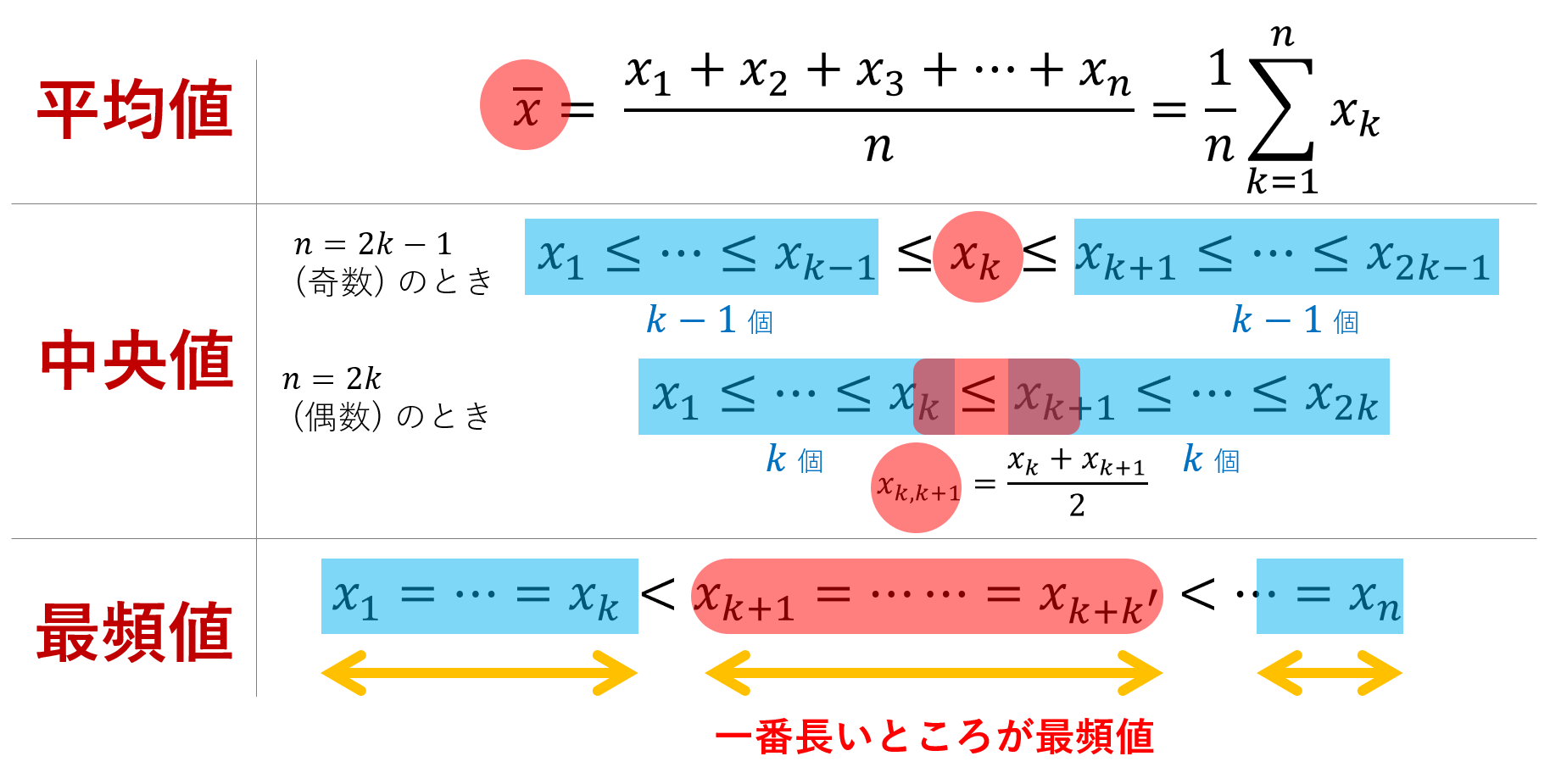
データにおいて,昇順に並べたときの真ん中の値(数が偶数個のときは真ん中の2つの値の平均)を中央値 (median) という。
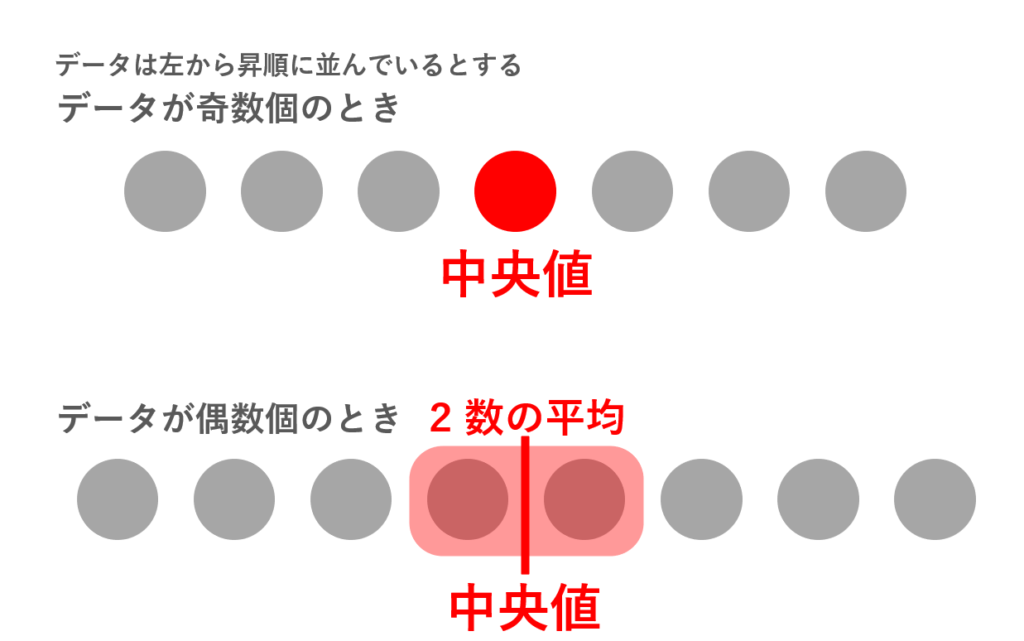
中央値については,以下でも解説しています。
四分位数・四分位範囲・四分位偏差
さて,準備は整いました。四分位数・四分位範囲・四分位偏差を定義しましょう。
定義(四分位数・四分位範囲・四分位偏差)
データを昇順に並べたとき,小さいものから25%の値 \color{red}\boldsymbol{ Q_1} を第一四分位数 (first quartile; lower quartile),50%の値 \color{red}\boldsymbol{Q_2} を第二四分位数 (second quartile) または中央値 (median),75%の値 \color{red}\boldsymbol{ Q_3} を第三四分位数 (third quartile; higher quartile) という。
\color{red}\boldsymbol{Q_3-Q_1} を四分位範囲 (interquartile range; IQR), \color{red}\boldsymbol{ \dfrac{Q_3-Q_1}{2}} を四分位偏差 (interquartile deviation) という。
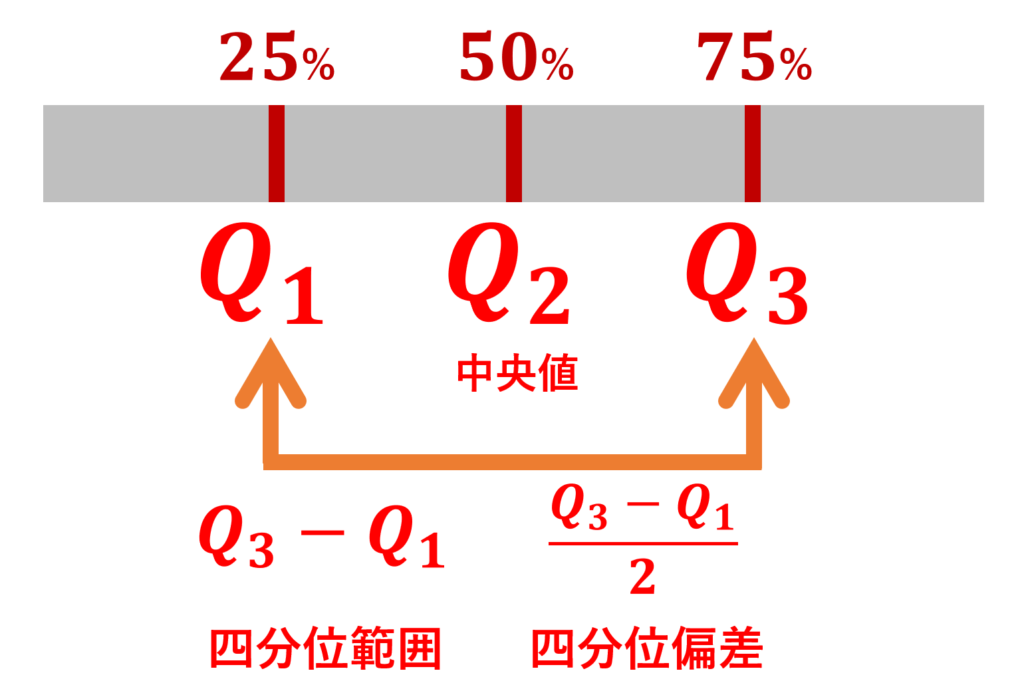
第二四分位数は中央値と同じです。
注意として,小さいものから25% 75%の解釈は何通りかあり,ばらつきがあります。ここでは,高校の検定教科書で紹介されている定義を紹介しましょう。データは左から昇順に並んでいるものとします。
まず,データが奇数個の場合を考えましょう。第二四分位数 Q_2 は中央値ですから,上で復習したとおりです。そして,真ん中のものを含まない小さい値と大きい値のブロックに分け,小さい方のブロックの中央値を第一四分位数 Q_1,大きい方のブロックの中央値を第三四分位数 Q_3 とします。
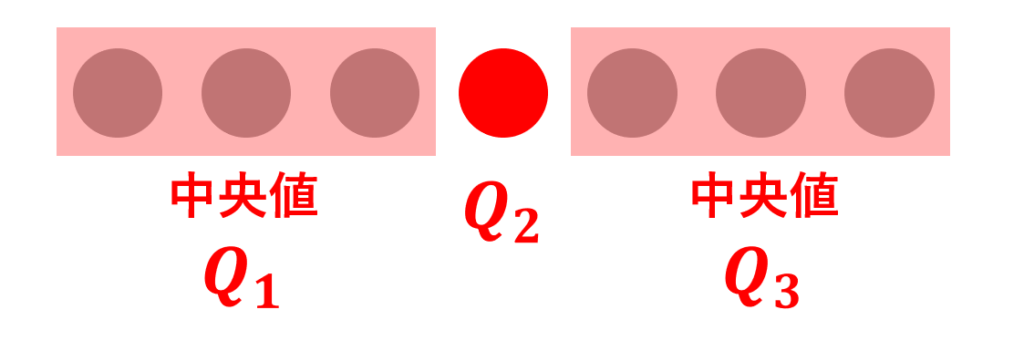
データが偶数個の場合について考えます。第二四分位数 Q_2 は中央値ですから真ん中の値2つの平均値ですね。そして,偶数個のデータをちょうど小さい値と大きい値のブロックに真っ二つに分け,小さい方のブロックの中央値を第一四分位数 Q_1,大きい方のブロックの中央値を第三四分位数 Q_3 とします。
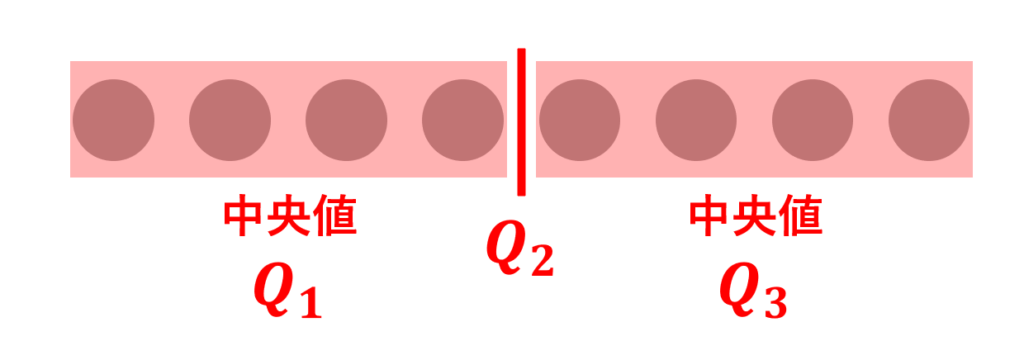
これが,オーソドックスな四分位数の定義です。
四分位数・四分位範囲・四分位偏差の具体例
例1.
データが 0,10,30, 30, 50, 60, 80, 90,100 であるとき,
\color{red}\begin{aligned} Q_1&= 20, \\ Q_2&= 50, \\ Q_3&= 85\end{aligned}
である。四分位範囲は Q_3-Q_1 = 85-20=65,四分位偏差は \dfrac{Q_3-Q_1}{2}=\dfrac{65}{2} = 32.5 となる。
実際に Q_1, Q_2,Q_3 求めるときは,まず Q_2 から考えるとよいでしょう。
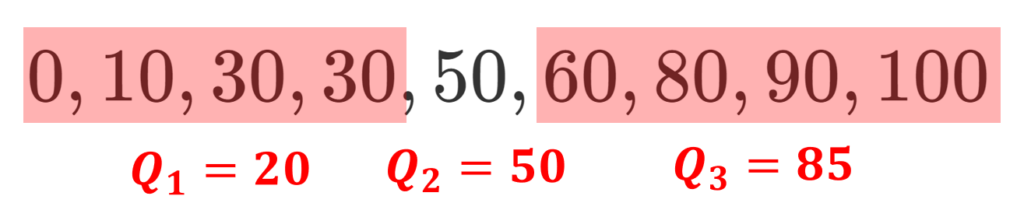
例2.
データが 0,1,1,2, 3, 5, 8, 9, 9,10 であるとき,
\color{red}\begin{aligned} Q_1&= 1, \\ Q_2&= 4, \\ Q_3&= 9\end{aligned}
である。 四分位範囲は Q_3-Q_1 = 9-1=8,四分位偏差は \dfrac{Q_3-Q_1}{2}=\dfrac{8}{2} = 4 となる。
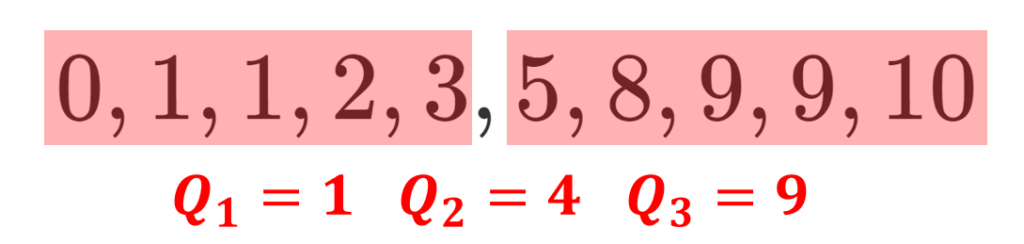
四分位数のその他の定義
「四分位数の定義にはばらつきがある」といいましたが,ここでは別の定義を簡単に紹介しましょう。
- 上の定義では,データ数が奇数の場合は真ん中の値を除いて2つのブロックに分けましたが,真ん中の値を含めて2つのブロックに分け,それぞれの中央値を考えるやり方があります。データ数が偶数のときは上の定義と同じです。
- データ数が偶数のときは上の定義と同じで,奇数のときはデータ x_1\le \dots\le x_{n} の数が n=4k+1 のとき, Q_1=\dfrac{x_n+3x_{n+1}}{4},Q_3=\dfrac{3x_{3n+1}+x_{3n+2}}{4} とし, n=4k+3 のときは Q_1=\dfrac{3x_{n+1}+x_{n+2}}{4}, Q_3=\dfrac{x_{3n+2}+3_{3n+3}}{4} とするやり方があります。
四分位数はデータの概要を知りたいだけですから,実際のところ,この辺の定義の違いはあまり気にしなくて良いです。
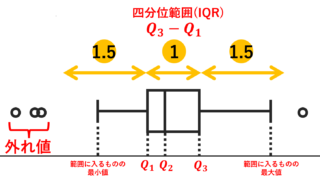
四分位数から箱ひげ図へ
最小値・第一四分位数・中央値(第二四分位数)・第三四分位数・最大値の五つを用いて,データのばらつきを表すことを五数要約 (five-number summary) といいます。
五数要約を図にしたものが,箱ひげ図 (box plot) といいます。箱ひげ図については,以下で解説しています。