散布図とは～定義を図解～

散布図とは，座標平面上に点をかくようにしてデータを可視化するものです。数値を2つずつ持つデータにおいて，その関連性を把握するために用います。

散布図について，その定義と具体例を確認しましょう。

散布図とは

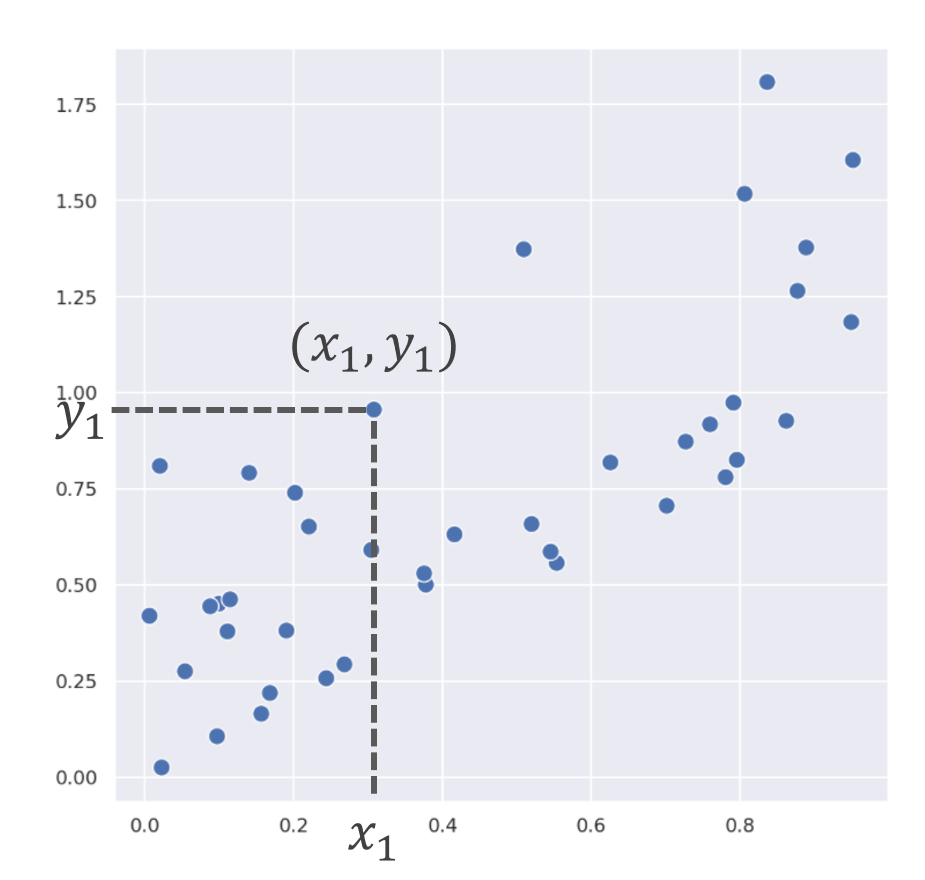
座標平面に (x,y) をたくさん描いている感じですね。特にこのことを，データを散布図にプロット (plot) するといいます。

一応具体例を見ておきましょう。以下のような，数学と理科のテストの点数データがあったとします。同じ列は同じ人の点数です。

それを散布図にプロットしたものが以下です。横軸が数学の点数で，縦軸が理科の点数です。

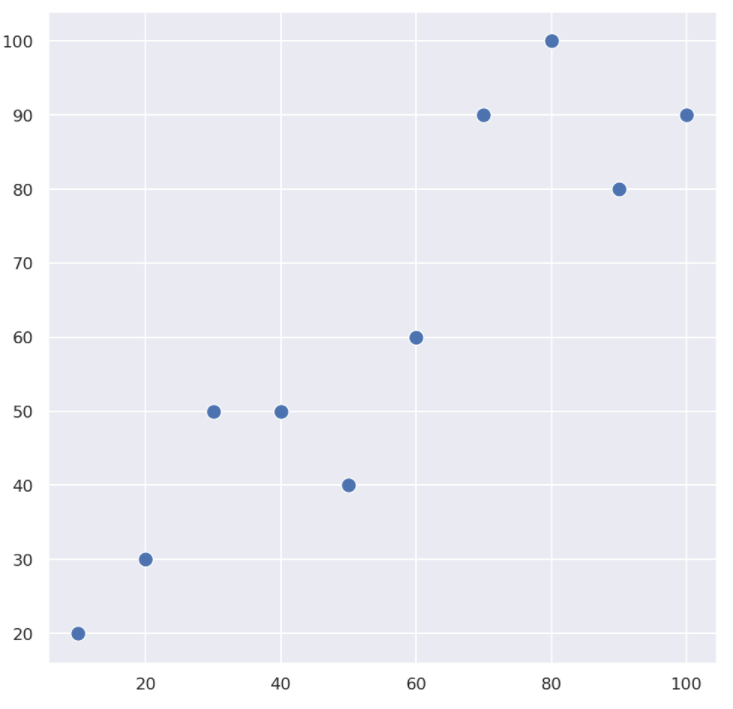
散布図からデータの相関へ

散布図はデータ (x,y) の関係性（相関; correlation）を把握するのに有用です。

たとえば，上の例の散布図を見ると，おおよそ左下から右上に分布しているのが分かると思います。これを大まかに捉えると，「数学の点数が良いほど理科の点数も良い」といえるでしょう。

データの相関について詳しくは別途解説しましょう。