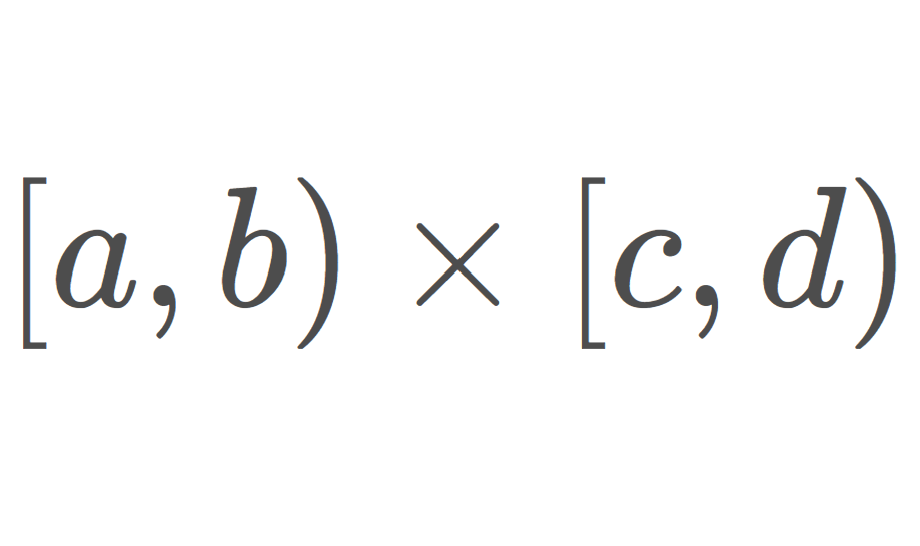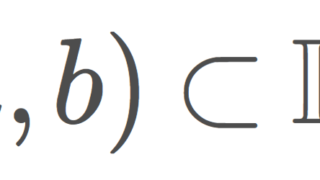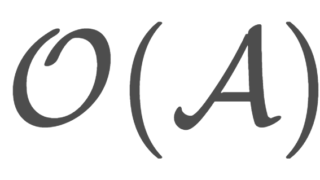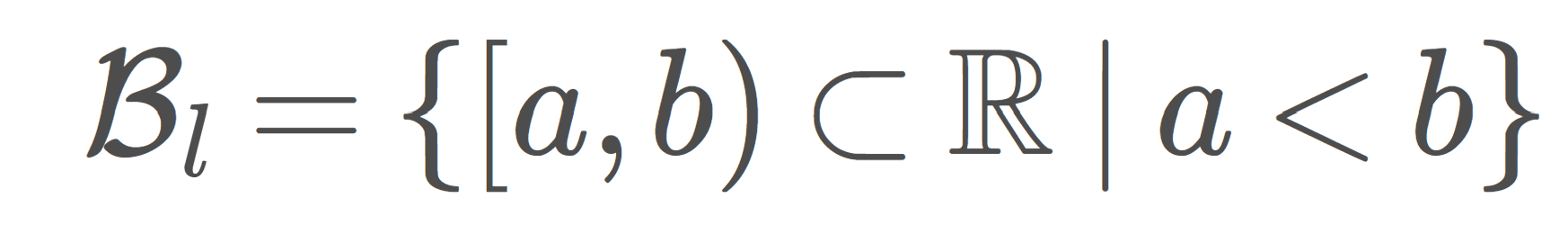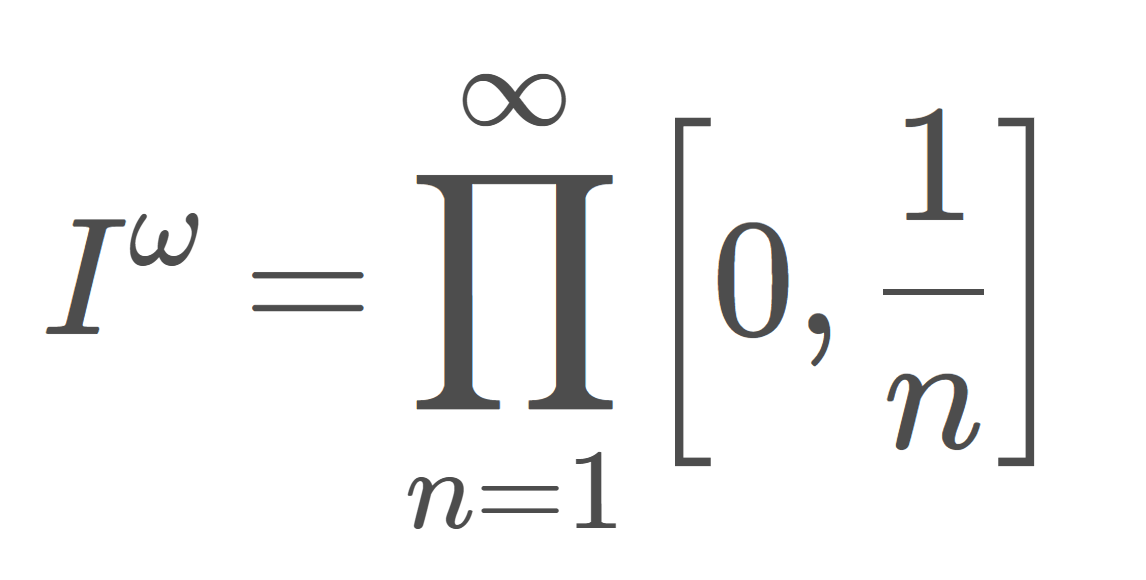ゾルゲンフライ平面とは， \R^2 上に入る，通常の位相より大きい位相で，ゾルゲンフライ直線2つの直積で表される位相空間です。
ゾルゲンフライ平面は， T_3 空間（あるいは正則空間）だが， T_4 空間 (あるいは正規空間）でない例としても有名です。ゾルゲンフライ平面の定義と性質を解説しましょう。
ゾルゲンフライ平面の定義
ゾルゲンフライ平面の定義の前に，ゾルゲンフライ直線と呼ばれる位相空間の定義をしておきましょう。
ゾルゲンフライ直線については，以下の記事で詳しく解説しています。
定義（ゾルゲンフライ平面）
(\R, \mathcal{O}_l) をゾルゲンフライ直線とするとき，その直積位相空間 (\R, \mathcal{O}_l)\times (\R, \mathcal{O}_l) をゾルゲンフライ平面 (Sorgenfrey plane) という。
ゾルゲンフライ平面とは，
\Large \mathcal{B}=\{ [a,b)\times [c, d) \mid a,b,c,d\in\R\}
を開基とする位相ともいえます。
ゾルゲンフライ平面の性質
ゾルゲンフライ平面の性質を，可算公理・分離公理・コンパクト性・連結性に分けて解説します。ゾルゲンフライ直線の性質とも比較しましょう。
L が閉集合であることは簡単です。(x,y)\in \mathbb{S}^2\setminus L に対し，ある \varepsilon>0 が存在して， [x, x+\varepsilon)\times [y, y+\varepsilon)\cap L=\emptyset とできるので， \mathbb{S}^2\setminus L は開集合です。よって， L は閉集合です。
ゾルゲンフライ平面と可算公理
証明は，ゾルゲンフライ直線のときとほぼ同じです。たとえば，可分性については， \{ (x, y)\mid x, y\in \mathbb{Q}\} が \mathbb{S}^2 上稠密のため，示せます。
なお， L\subset \mathbb{S}^2 は非可算な離散空間のため，可分ではありません。これは，可分な部分空間が可分とは限らないことの例になっています。
ゾルゲンフライ平面と分離公理
| T_0, T_1, T_2 (ハウスドルフ空間) | T_3 | T_4,T_5 | |
|---|---|---|---|
| ゾルゲンフライ直線 | 〇 | 〇 | 〇 |
| ゾルゲンフライ平面 | 〇 | 〇 | × |
本記事では， T_0 から T_5 は以下のように定義しています。この定義は文献によって変わりますから，注意してください。
| 名称 | 定義 |
|---|---|
| T_0 コルモゴロフ空間 (Kolmogorov space) | 任意の異なる2点 x,y\in X に対して， x\in O_x,\, y\notin O_x となる開集合 O_x または x\notin O_y,\, y\in O_y となる開集合 O_y の少なくとも一方が取れる |
| T_1 | 任意の異なる2点 x,y\in X に対して， x\in O_x,\, y\notin O_x となる開集合 O_x と x\notin O_y, \,y\in O_y となる開集合 O_y の両方が取れる |
| T_2 ハウスドルフ空間 (Hausdorff space) | 任意の異なる2点 x,y\in X に対して， x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset となる開集合 O_x, O_y が取れる |
| T_3 | 任意の閉集合 F と任意の点 x\in X\setminus F に対して， F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset となる開集合 O_F, O_x が取れる |
| T_4 | 任意の2つの互いに素な空でない閉集合 F,G\subset X に対して， F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset となる開集合 O_F, O_G が取れる |
| T_5 | \overline{A}\cap B=A\cap \overline{B}=\emptyset をみたす任意の2つの空でない集合 A,B\subset X に対して， A\subset O_A,\, B\subset O_B,\, O_A\cap O_B=\emptyset となる開集合 O_A, O_B が取れる |
定義から明らかに T_2\implies T_1\implies T_0 であり，また T_5\implies T_4 です。
証明
T_0,T_1, T_2 であることについて
T_2 空間（ハウスドルフ空間）の直積もまた T_2（ハウスドルフ）である(→直積位相とは～定義・具体例・性質～)。ゾルゲンフライ直線が T_2 なので，ゾルゲンフライ平面もそうである。
T_3 であることについて
T_3 空間の直積もまた T_3 である。ゾルゲンフライ直線が T_3 なので，ゾルゲンフライ平面もそうである。
T_4,T_5 でないことについて
以下では， \aleph_0 を可算濃度とし， \aleph で連続体濃度を表すとする。また， \R には通常の位相が入っているとする。 L は非可算な離散空間なので，連続関数 f\colon L\to \R の取り方は 2^{\aleph} だけある。
\mathbb{S}^2 が T_4 (あるいは正規空間) だと仮定する。このとき，ティーツェの拡張定理 (Tietze’s extension theorem) により，連続関数 f\colon L\to \R を拡張して連続関数 f\colon \mathbb{S}^2\to \R を作ることができ，その作り方は 2^{\aleph} 以上ある。一方で， \mathbb{S}^2 は可分なので，実際の取り方は 2^{\aleph_0} 以下である。これは矛盾している。よって， T_4 でないことが示せた。これにより， T_5 でもない。
なお，
\begin{aligned} L_1&=\{ (x, -x)\mid x\in \mathbb{Q}\} \\ L_2&= \{ (x, -x)\mid x\in \mathbb{R}\setminus \mathbb{Q}\} \end{aligned}
とすると， L_1, L_2\subset \mathbb{S}^2 はどちらも閉集合だが，開集合で分離できないことが証明できる。
証明終
T_0 から T_3 までは，元の空間が T_i ならば直積空間も T_i だといえますが， T_4, T_5 は，直積空間が T_4, T_5 になるとは言えません。特に，正則空間 (regular space) の直積は正則ですが，正規空間 (normal space) の直積は正規とは言えません。ゾルゲンフライ直線とゾルゲンフライ平面は，その代表的な例です。
ゾルゲンフライ平面とコンパクト性
コンパクト性に関する用語の定義は以下です。
| 名称 | 定義 |
|---|---|
| コンパクト (compact) | 任意の開被覆が有限部分被覆をもつ |
| 点列コンパクト (sequentially compact) | 任意の点列が収束部分列をもつ |
| 局所コンパクト (locally compact) | 任意の点がコンパクトな近傍をもつ |
| σコンパクト (σ-compact) | コンパクト集合の可算和でかける空間 |
| リンデレーフ (Lindelöf) | 任意の開被覆が可算部分被覆をもつ |
| パラコンパクト (paracompact) | 任意の開被覆が局所有限な(すなわち，各点ごとに有限個の集合でしか覆われていない近傍をもつような)部分被覆をもつ |
| メタコンパクト (metacompact) | 任意の開被覆が点有限な(すなわち，各点ごとに有限個の集合でしか覆われていない)部分被覆をもつ |
コンパクトでないこと・点列コンパクトでないこと。σコンパクトでないこと・局所コンパクトでないことは，ゾルゲンフライ直線のときの証明とほぼ同じように考えればよいです。メタコンパクトでないことが示せれば，パラコンパクトでないことは定義から明らかです。
以上を踏まえ，リンデレーフでないこと・メタコンパクトでないことを示しましょう。
リンデレーフでないこと・メタコンパクトでないことの証明
\begin{aligned}&\{ \mathbb{S}^2\setminus L\} \\&\cup\{ [x, x+1)\times [-x, -x+1)\mid x\in \R\} \end{aligned}
は \mathbb{S}^2 の開被覆であるが，一つでも欠ければ開被覆にならないため，リンデレーフでない。また，この被覆は点有限でないので，メタコンパクトでもない。
証明終
ゾルゲンフライ平面と連結性
| 連結 | 完全不連結 | |
|---|---|---|
| ゾルゲンフライ直線 | × | 〇 |
| ゾルゲンフライ平面 | × | 〇 |
ゾルゲンフライ平面が連結でなく，さらに完全不連結であることは，ゾルゲンフライ直線がそうであることの証明とほぼ同じです。
