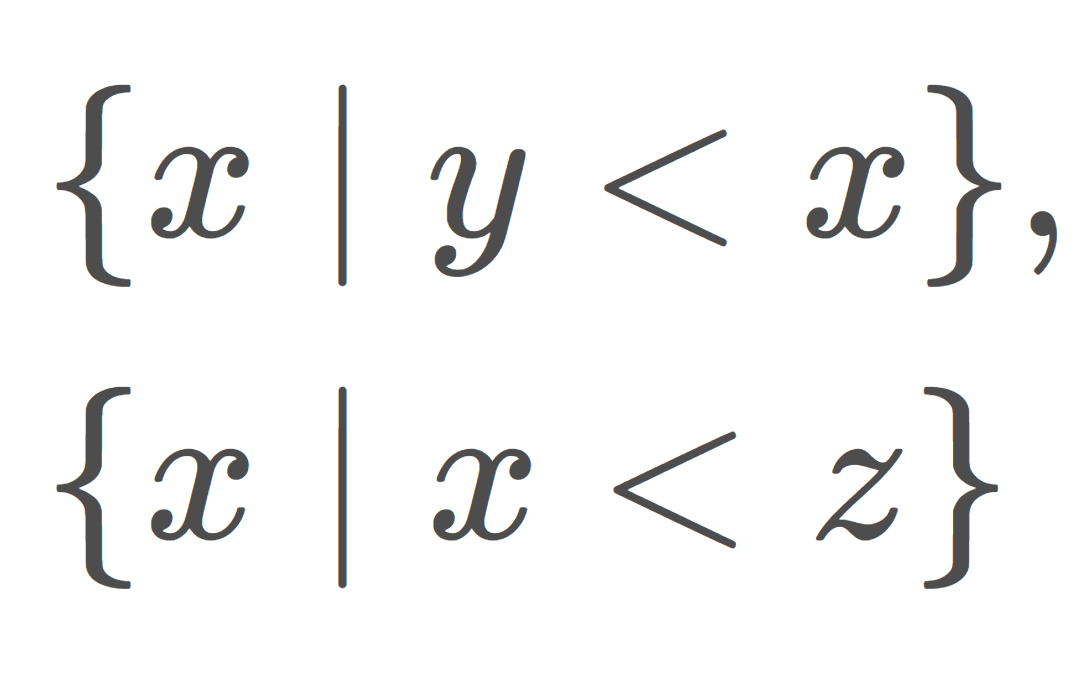順序位相の定義と順序数における順序位相の性質

順序位相とは，全順序集合における，順序によって定まる位相のことで，開区間 $(\alpha, \beta)$ は開集合です。

順序位相についての定義を紹介し，また順序数における順序位相について掘り下げて考えます。

順序位相の定義と簡単な例
順序数における順序位相
関連する記事
参考

順序位相の定義と簡単な例

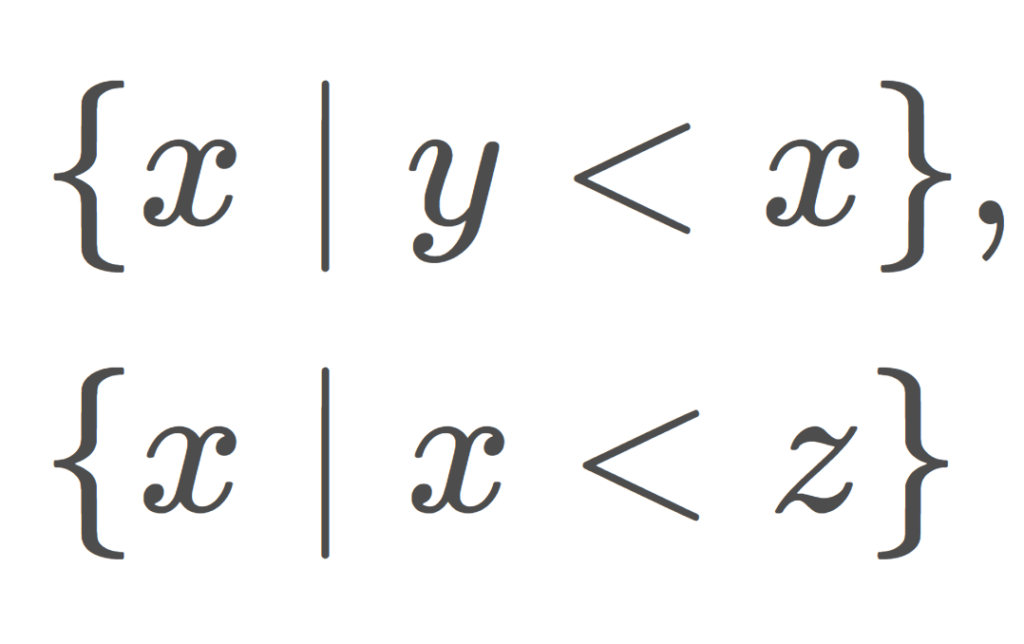
順序位相は，一般に全順序集合上で定義されます。

定義（順序位相）

$X$ を全順序集合とする。このとき，各 $y,z\in X$ に対して，

\Large\color{red} \{ x\mid y<x\},\quad \{ x\mid x<z\}

の形の集合たちを準開基とする位相を順序位相 (order topology) という。

$X$ のどの元よりも大きい元 $\infty$ と小さい元 $-\infty$ を定めると， $(y,\infty), (-\infty, z)$ を準開基とする位相と言ってもよいでしょう。

定義より， $a<b$ に対し， $(a,b)=\{ x\mid a<x<b\}$ は開集合です。また， $X$ に最小元 $m\in X$ が存在するときは， $b\in X$ に対し， $[m, b)= \{ x\mid x<b\}$ も開集合です。また最大元 $n\in X$ が存在するときは， $(a, n]=\{ x\mid a<x\}$ も開集合です。

いくつか簡単な例を確認しておきましょう。

例1( $\R$ ).

実数の集合 $\R$ における通常の順序による順序位相は，通常の位相と等しい。

$\R$ における通常の位相の開基は開区間 $(a,b)\;(a,b\in\R)$ たちです。

例2( $\mathbb{N}$ ).

自然数の集合 $\mathbb{N}=\{0,1,2,\ldots\}$ における通常の順序による順序位相は，離散位相である。

任意の $n\in\mathbb{N}$ において， $\{n\}=(n-1, n+1)$ が開集合になるため，離散位相です。

例3( $\mathbb{N}\cup \{\infty\}$ ).

任意の $n\in\mathbb{N}$ に対し， $n<\infty$ となる順序を入れた $\mathbb{N}\cup \{\infty\}$ における順序位相は， $\mathbb{N}$ の1点コンパクト化に等しい。すなわち，各 $n\in\mathbb{N}$ に対し， $\{n\}$ と $(n,\infty]$ を開集合とする最小の位相である。

$\{\infty \}$ は開集合ではないため，例3.の位相は離散位相ではありません。

順序数における順序位相

整列集合である順序数たちおける順序位相を考え，その性質を証明しましょう。以下では，順序数の基本的な話は既知とします。以下の記事を参照してください。

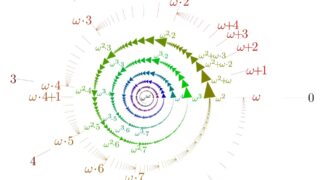
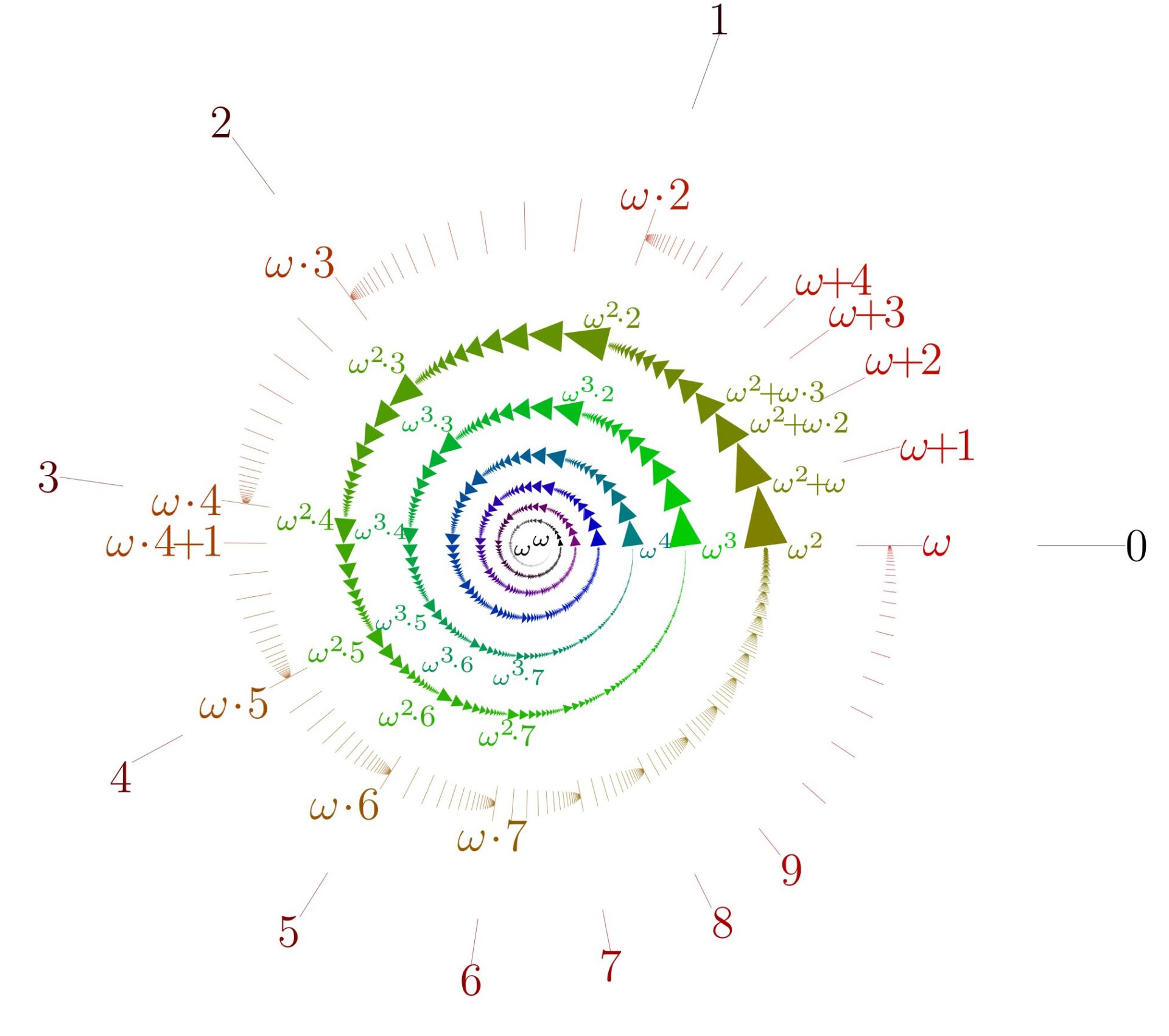
以下で， $\color{red}\Large \omega_1$ を最小の非可算順序数とし， $\color{red}\Large \Gamma$ を， $\Gamma<\omega_1$ をみたす極限順序数とします(たとえば上の記事における $\omega$ や $\omega^2$ や $\omega^\omega$ など)。極限順序数とは， $\alpha+1=\Gamma$ となる順序数 $\alpha$ がとれないような順序数を言います。 $\Gamma$ は可算順序数です。

整列集合 $[0, \Gamma),[0, \Gamma], [0, \omega_1),[0, \omega_1]$ に入る順序位相を考えましょう。この順序位相は， $\{0\}$ と，

(\alpha, \beta] = (\alpha,\beta+1)=\{ x\mid \alpha<x<\beta+1\}

を開基とする位相です。まずは紹介する性質をまとめておきましょう。

	$[0, \Gamma)$	$[0, \Gamma]$	$[0, \omega_1)$	$[0,\omega_1]$
第一可算	〇	〇	〇	×
第二可算	〇	〇	×	×
可分	〇	〇	×	×
距離化可能	〇	〇	×	×
$T_0,T_1,T_2,T_3, T_4, T_5$ 空間	〇	〇	〇	〇
コンパクト	×	〇	×	〇
σコンパクト・リンデレーフ	〇	〇	×	〇
点列コンパクト・可算コンパクト	×	〇	〇	〇
パラコンパクト・メタコンパクト	〇	〇	×	〇
強局所コンパクト	〇	〇	〇	〇
完全不連結	〇	〇	〇	〇

順番に考えますが，ここで大事になってくるのは次の定理です。

定理1（可算集合では $\omega_1$ に到達できない）

$A\subset [0,\omega_1)$ が可算集合のとき， $\sup A<\omega_1$ である。

これにより，任意の点列 $\{x_n\}\subset [0,\omega_1)$ は $\omega_1$ に収束し得ないことがわかる。

$\sup A =\min \{ \zeta\mid \forall a\in A, \, a\le \zeta\}$ です。証明は順序数に関する基本的なことで行っています。この定理は既知とします。

順序数の順序位相と可算公理

	$[0, \Gamma)$	$[0, \Gamma]$	$[0, \omega_1)$	$[0,\omega_1]$
第一可算	〇	〇	〇	×
第二可算	〇	〇	×	×
可分	〇	〇	×	×
距離化可能	〇	〇	×	×

距離化可能性は可算公理とは言えないかもしれませんが，同時に考えましょう。

証明

第一可算について

$\zeta \in [0,\omega_1)$ とする。 $\{\alpha \mid \alpha<\zeta\}$ は可算集合なので， $\{(\alpha, \zeta]\mid \alpha<\zeta\}$ は可算な基本近傍系である。よって， $[0,\omega_1)$ は第一可算である。 $[0,\Gamma), [0,\Gamma]$ も同様である。

一方で， $\omega_1\in [0,\omega_1]$ は可算な基本近傍系をもたない。これは， $\mathcal{B}_{\omega_1}=\{(\alpha_n, \omega_1]\}_n$ を考えると，定理1より， $\sup_n \alpha_n<\omega_1$ なので， $\left( \sup_n \alpha_n+1, \omega_1\right]$ に含まれる $\mathcal{B}_{\omega_1}$ の元は存在しないことから分かる。

第二可算について

$[0,\Gamma), [0,\Gamma]$ は第一可算かつ可算集合なので，第二可算である。

$[0, \omega_1)$ は第二可算でないことを示そう。 $\mathcal{B}=\{[\alpha_n, \beta_n]\}_n$ とすると，定理1より， $\sup_n \beta_n+1<\omega_1$ であるが， $\mathcal{B}$ は $\sup_n \beta_n+1$ を被覆していない。よって第二可算でない。

可分性について

$[0,\Gamma), [0,\Gamma]$ は可算集合なので可分である。

$[0, \omega_1)$ について考えよう。 $A=\{\alpha_n\}$ を可算集合とすると，定理1より $\sup_n \alpha_n <\omega_1$ であり， $\sup \alpha_n +1\notin \overline{A}$ なので， $[0, \omega_1)$ は可分でない。また， $[0, \omega_1]$ について， $\{\omega_1\}$ は閉集合であるから， $[0,\omega_1]=[0,\omega_1)\cup \{\omega_1\}$ も可分でない。

距離化可能性について

$[0, \Gamma),[0, \Gamma]$ は第二可算かつ正規空間（ $T_2, T_4$ 空間）であるので，ウリゾーンの距離化定理により，距離化可能である。

また，距離化可能であれば，コンパクト性と点列コンパクト性は同値だが，後で示すように $[0,\omega_1)$ は点列コンパクトだがコンパクトでないので，距離化可能でない。また， $[0,\omega_1)$ は $[0,\omega_1]$ の部分空間なので， $[0,\omega_1]$ も距離化可能でない。

証明終

順序数の順序位相と分離公理

	$[0, \Gamma)$	$[0, \Gamma]$	$[0, \omega_1)$	$[0,\omega_1]$
$T_0,T_1,T_2,T_3, T_4, T_5$ 空間	〇	〇	〇	〇

分離公理は，本サイトでは以下の定義を採用しています。これは文献によって異なります。

名称	定義
$T_0$ コルモゴロフ空間	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x,\, y\notin O_x$ となる開集合 $O_x$ または $x\notin O_y,\, y\in O_y$ となる開集合 $O_y$ の少なくとも一方が取れる
$T_1$	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x,\, y\notin O_x$ となる開集合 $O_x$ と $x\notin O_y, \,y\in O_y$ となる開集合 $O_y$ の両方が取れる
$T_2$ ハウスドルフ空間	任意の異なる2点 $x,y\in X$ に対して， $x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset$ となる開集合 $O_x, O_y$ が取れる
$T_3$	任意の閉集合 $F$ と任意の点 $x\in X\setminus F$ に対して， $F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset$ となる開集合 $O_F, O_x$ が取れる
$T_4$	任意の2つの互いに素な閉集合 $F,G\subset X$ に対して， $F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset$ となる開集合 $O_F, O_G$ が取れる
$T_5$	$\overline{A}\cap B=A\cap \overline{B}=\emptyset$ をみたす任意の2つの集合 $A,B\subset X$ に対して， $A\subset O_A,\, B\subset O_B,\, O_A\cap O_B=\emptyset$ となる開集合 $O_A, O_B$ が取れる

一般に，全順序集合における順序位相は，上の全ての分離公理をみたすことが知られています。証明は省略します。

順序数の順序位相とコンパクト性

	$[0, \Gamma)$	$[0, \Gamma]$	$[0, \omega_1)$	$[0,\omega_1]$
コンパクト	×	〇	×	〇
σコンパクト・リンデレーフ	〇	〇	×	〇
点列コンパクト・可算コンパクト	×	〇	〇	〇
パラコンパクト・メタコンパクト	〇	〇	×	〇
強局所コンパクト	〇	〇	〇	〇

コンパクトにまつわる定義の確認をしておきましょう。

名称	定義
コンパクト (compact)	任意の開被覆が有限部分被覆をもつ
σコンパクト (σ-compact)	コンパクト集合の可算和でかける空間
リンデレーフ (Lindelöf)	任意の開被覆が可算部分被覆をもつ
点列コンパクト (sequentially compact)	任意の点列が収束部分列をもつ
可算コンパクト (countably compact)	任意の可算開被覆が有限部分被覆をもつ
パラコンパクト (paracompact)	任意の開被覆が局所有限な(すなわち，各点ごとに有限個の集合でしか覆われていない近傍をもつような)開細分被覆をもつ
メタコンパクト (metacompact)	任意の開被覆が点有限な(すなわち，各点ごとに有限個の集合でしか覆われていない)開細分被覆をもつ
強局所コンパクト (strong locally compact)	任意の点がコンパクトな閉近傍をもつ

証明

コンパクト性について

$[0, \Gamma)$ がコンパクトでないことは， $\{ [0,\alpha)\mid \alpha<\Gamma\}$ が有限部分被覆をもたないことからわかる。 $[0, \omega_1)$ がコンパクトでないことも同様。

$[0,\omega_1]$ がコンパクトであることを示す。まず，この集合は任意の $A\subset [0,\omega_1]$ に対し，

\sup A = \min\{ \zeta\in [0,\omega_1]\mid \forall a\in A, \,a\le \zeta \}

が存在することに注意する。実際，右辺の集合は $\omega_1$ を元にもつため空でなく，整列集合なので右辺の集合は最小元が存在するからである。

$\mathcal{C}$ を開被覆とする。「 $[0,\alpha)$ が $\mathcal{C}$ に属する有限個の開集合で覆える」ような $\alpha \in [0,\omega_1]$ 全体の集合を $S$ とする。 $s= \sup S$ とする。 $\mathcal{C}$ が開被覆であることと，開基の定義より，ある開集合 $U\in\mathcal{C}$ と $\alpha,\beta\in [0,\omega_1]$ が存在して，

s\in (\alpha, \beta]\subset U

となる。したがって， $\beta\in S$ もいえる。背理法で，仮に $s< \omega_1$ とする。 $\beta\in S$ と $s=\sup S$ より， $s=\beta$ である。このとき， $(\alpha, \beta]=(\alpha,\beta+1)$ より，さらに $\beta+1\in S$ となるが，これは矛盾している。したがって， $s=\omega_1$ であり，ゆえに $[0, \omega_1)$ を被覆する有限部分被覆が存在する。それに1点加えた $[0,\omega_1]$ を被覆する有限部分被覆も存在するから， $[0,\omega_1]$ はコンパクトである。