くし空間は, \R^2 における,連結性の議論で具体例に出される部分空間で,「くし」みたいな形をしています。定義と位相的性質を紹介しましょう。
くし空間(Comb Space)
定義(くし空間)
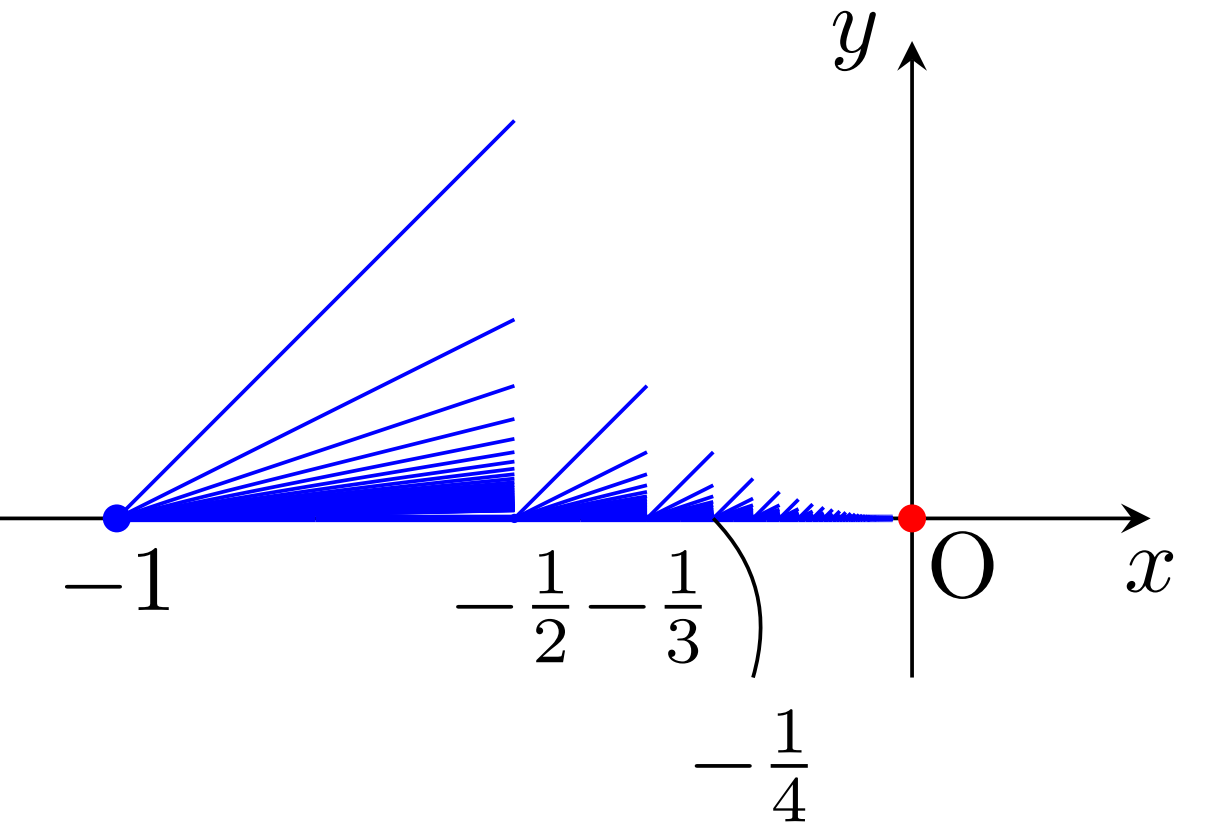
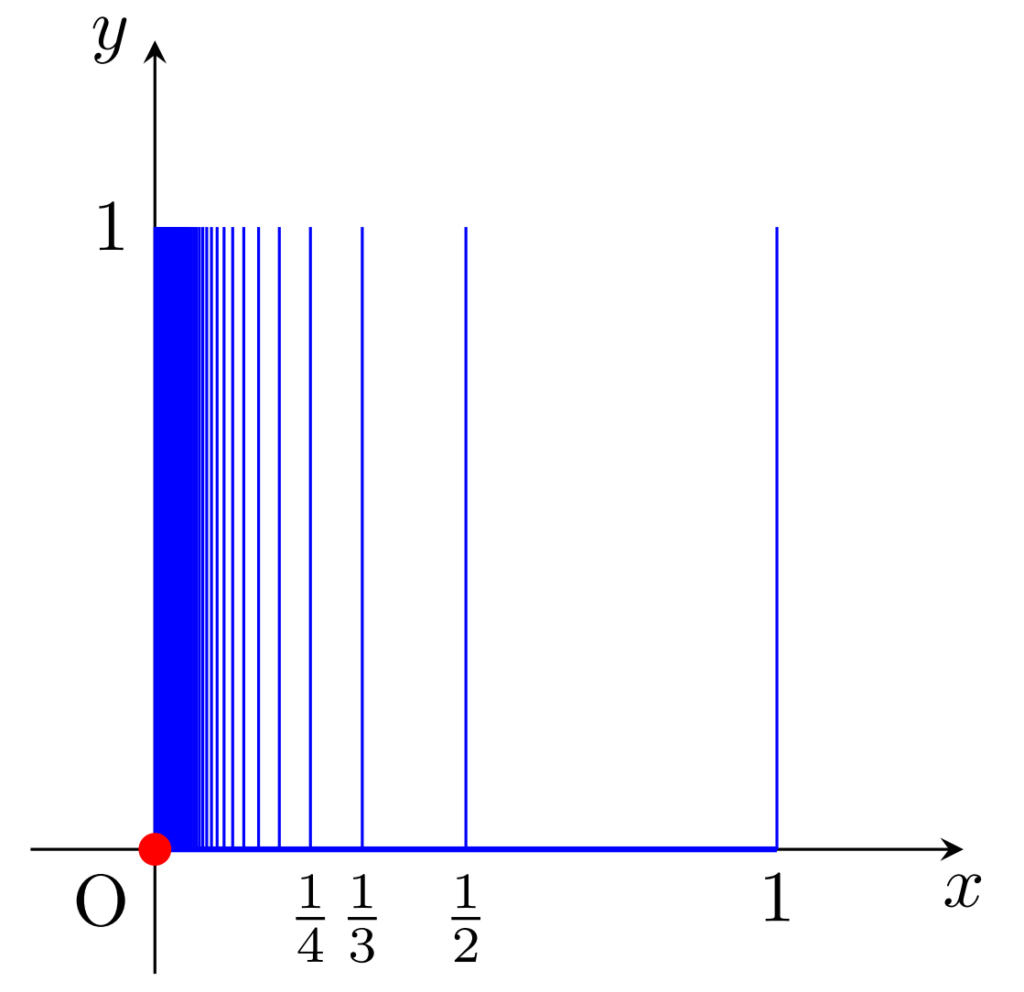
a\in \R に対し, \R^2 における部分集合を I_a =\{a\}\times [0,1]=\{(a, y)\mid 0\le y\le 1\} とする。
\color{red}\large C =I_0\cup \left(\bigcup_{n=1}^\infty I_{1/n}\right) \cup ([0,1]\times\{0\})
に \R^2 から定まる相対位相を入れた位相空間をくし空間 (comb space) という。
また, C\setminus\{(0,0)\} を,原点を除いたくし空間という。
くし空間の位相的性質
| くし空間 C | C\setminus \{(0,0)\} | |
|---|---|---|
| 第一可算・第二可算・可分 | 〇 | 〇 |
| 距離化可能 | 〇 | 〇 |
| T_0, T_1,T_2, T_3, T_4, T_5 空間 | 〇 | 〇 |
| コンパクト・点列コンパクト | 〇 | × |
| 局所コンパクト | 〇 | 〇 |
| 連結 | 〇 | 〇 |
| 弧状連結・弧連結 | 〇 | × |
| 局所連結 | × | × |
くし空間は連結・弧状連結ですが,局所連結でない空間として,そして,原点除いたくし空間は連結ですが弧状連結・局所連結でない空間として,よく例に挙げられます。
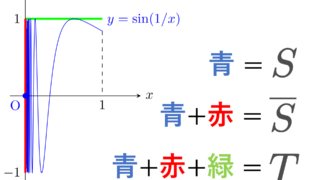
全ての性質は,位相幾何学者の正弦曲線 (topologist’s sine curve)
\begin{aligned}S&=\left\{\left(x, \sin\frac{1}{x}\right)\middle| 0<x\le 1\right\}\cup \{(0,0)\} \\ \overline{S} &= S\cup \left(\{0\}\times [-1,1]\right) \\ T&=\overline{S}\cup \left([0,1]\times \{1\}\right) \end{aligned}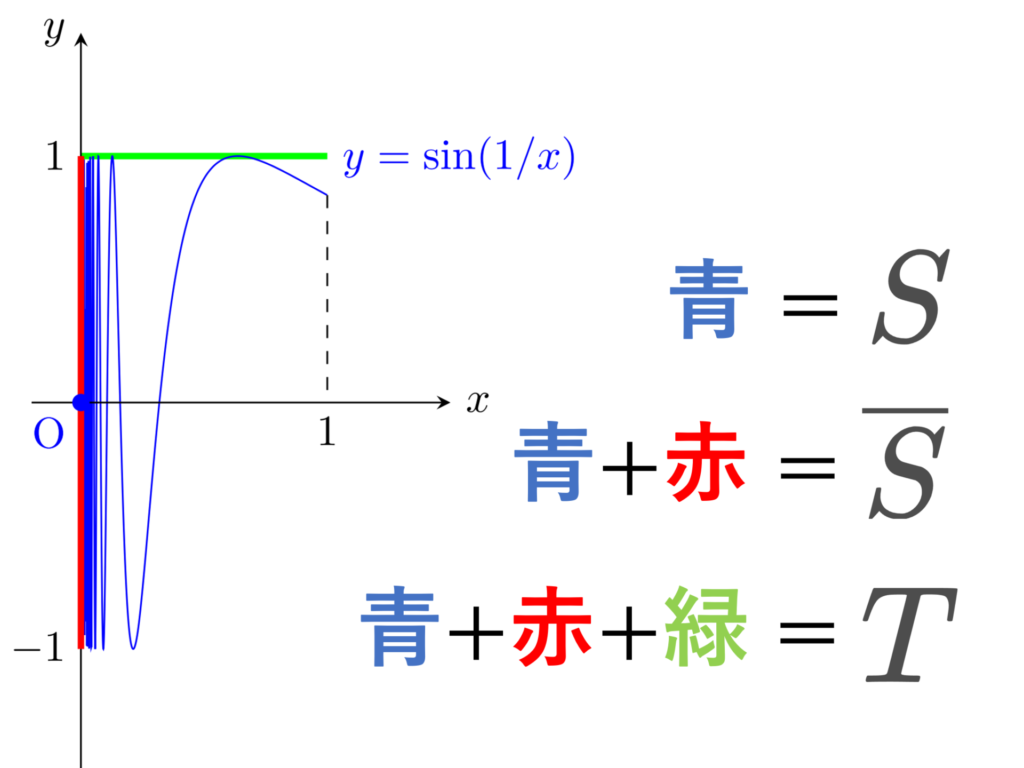
とほぼ同じですから,解説はそちらを参考にしてください。