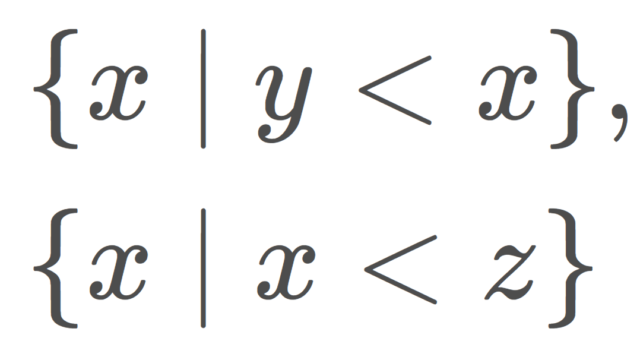 集合と位相
集合と位相 順序位相の定義と順序数における順序位相の性質
順序位相とは,全順序集合における,順序によって定まる位相のことで,開区間(α, β)は開集合です。順序位相についての定義を紹介し,また順序数における順序位相について掘り下げて考えます。
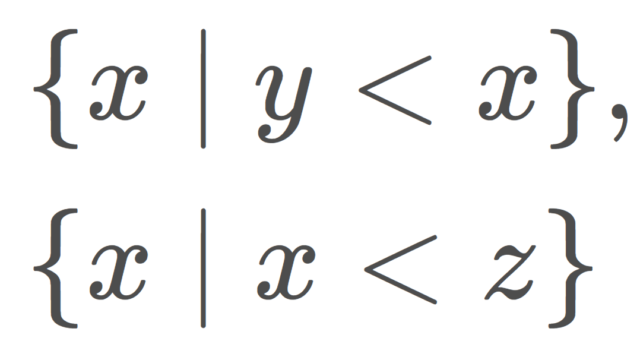 集合と位相
集合と位相 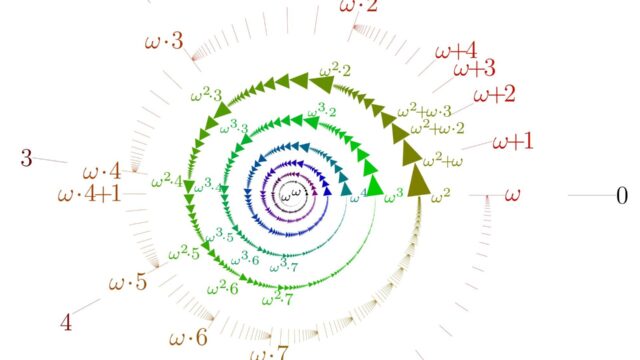 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相 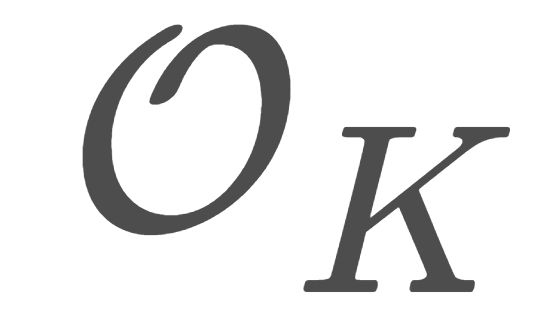 集合と位相
集合と位相 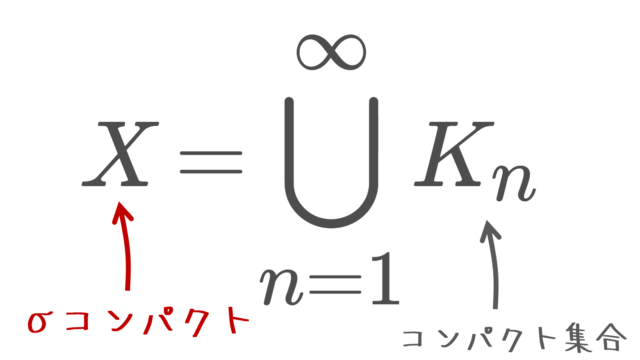 集合と位相
集合と位相 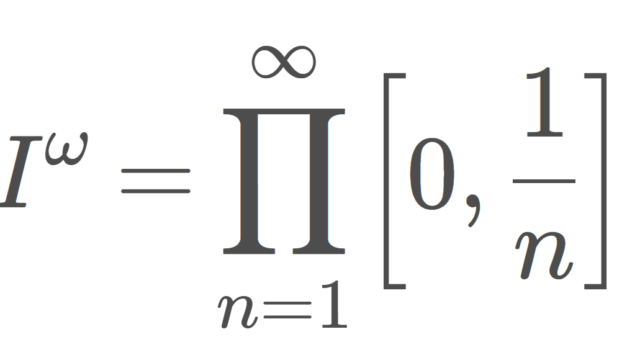 集合と位相
集合と位相